发现纯数学与物理之间的神密联系

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

一位杰出的数学家运用物理学中的概念研究了困惑人们数千年的数学问题，并取得了进展。

 

 

数学里面充满了超自然的数的系统，其中大部分人从来没有听说过，甚至理解起来有困难。但是有理数是家喻户晓的，它们是自然数和分数——这些有理数你从小学就知道了。但是对于数学家来说，最简单的问题往往最难理解。它们简单的就像一堵抗风墙，没有裂缝、突出物或者明显你可以抓住的某些东西。

 

牛津大学的一位叫金明迥的数学家，对于寻找哪些有理数可以解特定类型的方程特别感兴趣。几千年来无数数论学家挑战过这个问题。他们在解决问题方面进展甚微。当一个问题研究了很久却没答案，我们很自然的就认为唯一的出路就是有一个人能提出新的想法。这个人就是金明迥。

“即使我们已经研究了3000年，但研究这些问题依然没有太多的技术手段。所以任何人无论何时提出一个可靠的新方法去解决它都是一个大的进展，这就是金明迥所做的。”威斯康星大学的数学家乔丹·艾伦伯格（Jordan Ellenberg）评论道。

 

在过去的十年间，金明迥想出了一个非常新颖的方法----在看似无规律的有理数域寻找模式。他将这种方法写进论文里，发布在讨论会中，并将其传递给学生，现在学生们自己继续进行研究。但是他一直保留着一些东西， 他的思想正走向成熟，不是基于纯粹的数论，而是从物理中借用概念。对于金明迥来说，有理数解多少有点像光的轨迹。

 

如果这样的联系让你觉得像天方夜谭，那就对了，因为一些数学家也甚至和你有相同想法。由于这个原因，金炯明长期以来没有吐露这个想法。“我将它藏了起来，因为一直以来我多少会因为物理联系而不安，”他说。“数论学者是一群相当严谨刻板的人，物理的因素的加入有时使他们更加怀疑我做的数学。”

 

但是现在金明迥说他已经打算向世人表达他的想法。“我想这个改变单纯的是因为思想成熟起来了！”53岁的金明迥在我们交流这个故事的一封邮件的开头写到。

 

他最近已经举办了一场学术会议，邀请了数论学家和弦论学家。他也为还没有习惯于通过直接类比物理世界来思考数论问题的数学界写一篇文章去描述他的想法。

 

至今仍有一个绊脚石——数学和物理类比的最后一部分，金明迥仍需要继续攻克下去。他希望邀请更多的人去参与他的研究，特别是物理学家，他需要物理学家的帮助去完善它。

 

一个古老的挑战

 

方程的有理解深深地吸引着人们。找到方程的有理解，就像拼图块完美地落实到对应的位置那样令人满足。基于这样的理由，数学中很多著名的猜想都是关于方程有理解的。

 

有理数包含整数和任何可以表示为两个互素的整数之比的数。例如1，-4以及99/100.数学家对丢番图方程（Diophantine equation）——整系数多项式方程的有理数解特别感兴趣。就像x²+y²=1。公元3世纪，生活在古希腊亚历山大城的丢番图就研究了很多这样的方程。

 

有理解很难用全面的方法所找到，因为他们不遵循任何几何模式。考虑方程x²+y²=1。它的实数解是一个圆，拿走在这个圆上的所有不能表示为分数的点，所留下的就是有理解，而这样的解不会形成一个规则的形状。有理解是随机分布在圆周上的。

 

 

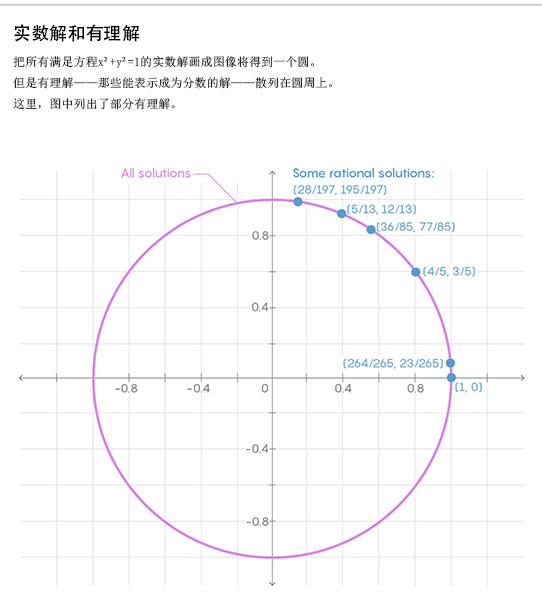
 “具有有理坐标点的条件根本不是几何条件。 你无法知道如果一些有理点满足某方程，它必须满足写什么条件”金明迥说。

 

有的方程，通常容易找到某个单一的有理解，甚至许多有理解。但对于不喜欢松散结果的数学家来说，他们对研究所有的有理解更有兴趣。这样问题就会难很多了。事实上，甚至是关于有理数最直白的结果，足以让你在数学圈出人头地。如同在1986年，一个名叫法尔廷斯(Gerd Faltings)的数学家荣获了数学最高荣誉的菲尔兹奖，他就是解决了一个叫莫德尔猜想(Mordell conjecture)）的问题，证明了一族特定的丢番图方程仅有有限多的有理解（而不是无限多解）。

 

法尔廷斯的证明在数论中是一个具有举足轻重的结果。但这也是数学家所说的“无用的证明”，事实上这意味着它没有精确计算出有理解的数量，更不用说找出它们了。从那以后，数学家开始寻找解决下一步的方法。有理点看起来就像一个方程的普通图像上的随机点。如果他们改变他们所研究问题的条件，数学家们希望这些点将看起来像一个星座一样，他们能以一些精确的方式去描述。但问题是，在已知的数学领域并没有给出这样的条件。

 

 “为了得到关于有理解的有效结果，人们当然会认为，解决这个问题需要一个全新的想法。”艾伦伯格说。

 

目前，关于新想法是什么样，有两个主要研究。一个来自于日本数学家望月新一，2012年，他在京都大学的教职员网页上发表了数百页复杂又新奇的数学成果。五年后，他的论文依然是高深莫测的。而另一个新想法就来自于金明迥。他试图在扩张的数论空间中思考有理数，在这其中隐藏的模式开始出现。

 

一个对称解

 

数学家通常说研究对象的对称性越好，就越容易研究。鉴于此，他们希望将丢番图方程的研究置于比问题本身产生的空间更对称空间中。如果他们能这样做，他们可以利用新的相关对称性去追踪他们所寻找的有理点。

 

为了见识一下对称性如何帮助数学家解决问题，画一个圆。可能你的目标是定义在圆上的所有点。对称性是一个有用的工具因为它创建了一个映射，可以让你从已知点的性质推出未知点的性质。

 

想象一下，你已经在下半圆找到了所有的有理点。因为圆是反射对称的，你可以水平直径为对称轴翻转下半圆的有理点(改变所有y坐标的符号)，于是一下子你就可以得到在上半圆的所有有理点。事实上，一个圆拥有丰富的对称性，即使知道一个单点的位置，结合对称知识，如果你需要找圆上的所有有理点，只要围绕原点无限旋转对称就可以得到。

 

但是如果你处理的几何对象有着高度无规律性，就像一个随机游走路径，你将需要努力去分别独立找出每一个点——这儿没有对称关系帮助你去将已知点映射到未知点。

 

数的集合也可以拥有对称性。集合的对称性越多，就越容易去理解——你可以应用对称性去发现未知的值。具有特定类型对称关系的数聚在一起形成一个“群”，数学家可以使用群的性质去理解包含在其中的所有的数。

 

一个方程的有理解集合不具有任何对称性也不形成一个群。从而使数学家们不可能一次性就发现所有的解。

 

从二十世纪40年代开始，数学家们开始探索一种方法去将丢番图方程的解放到一个拥有更多对称性的空间中去找。数学家沙博蒂(Claude Chabauty)发现在他构建的更大的几何空间的内部（通过一个被称为p进数（p- adic numbers）的扩张的全域），有理数形成了自己的对称子空间。他开始用这样的子空间与丢番图方程的图像联系起来。两个空间相交的点就是方程的有理解。

 

在二十世纪80年代，数学家科尔曼(Robert Coleman)对 沙博蒂的结果进行了改进。 在那之后的几十年里，科尔曼-沙博蒂方法成为数学家寻找丢番图方程有理解最有效的工具。但只有当方程的图像与更大的空间大小成比例时，它才起作用。当不成比例时，那么就很难精确找出方程曲线与有理数相交的点。

 

“如果你有一条曲线在空间内，而且有太多有理点，这些有理点集纠结在一起，你就很难区分哪些有理点在曲线上。”一位在加州大学圣地亚哥分校名叫凯德拉亚（Kiran Kedlaya）的数学家说。

 

于是，金明迥开始着手起这个问题了。为了在沙博蒂的基础上取得更进一步的成果，他希望去寻找一个甚至更大的空间去思考丢番图方程——一个有更多有理点分布的空间，于是他就可以研究更多不同种类丢番图方程的相交点。

 

空间的空间

 

如果你在寻找一个更大的空间，以及在思考如何沿着对称这条线索来寻找答案，借助于物理办法是个好的选择。

 

一般来说，在数学的意义上，一个空间是一个拥有几何或拓扑结构的点集。随意分散的一千个点不会形成空间，因为没有任何结构将他们联系在一起。但是对于一个球，由特殊的连续分布的点构成，它是一个空间。同样的环面、二维平面、或者我们生活中四维时空也是一个空间。

 

除了这些空间外，存在更多的风格迥异的空间，你可以把它看成“空间的空间”。举一个非常简单的例子，想象你有一个三角形——这是一个空间，那么继续想象所有可能的三角形，它们组成一个空间。在这个更大空间内的每一点代表一个特定的三角形，由它所表示的三角形的角的顶点的坐标。

 

这样的想法在物理中非常有用。在广义相对论的框架下，时间和空间不断演变，物理学家把每个时空看作是所有时空所组成的空间中的一个点。空间的空间在规范场论这个物理领域中出现过，这与物理学家在物理空间之上建立的场有关。这些场描述了你在空间中运动时，这些力如何起作用，如同你看到的电磁力和重力一样。你可以想象，在空间的每一个点上，这些场的构造都略有不同——而且所有这些不同的构造聚在一起形成了更高维度的“所有场的空间”中的点。

 

这个物理学中场的空间与金明迥在数论中提出的观点类似。为了便于理解，我们考虑一束光。物理学家想象光穿过高维的场空间。在这个空间中，光线将遵循“最小作用量原理”的路径——也就是从A到B所需最短时间的路径。这个原理解释了为什么当光从一个介质到另一种介质会弯曲——弯曲的路径花费的时间最少。

 

物理学中出现的这些更大的空间的空间具有额外的对称性，这些对称性并不存在于它们所代表的任何空间中。通过对称性可以找出特殊点，例如强调的时间最短路径。在另一种情况下以另一种方式构建，这些相同类型的对称可能会注重其他类型的点——如对应于方程的有理解的点。

理学中出现的这些更大的空间空间具有额外的对称性，这些对称性并不存在

 

对称性与物理之间的纠缠

 

数论没有粒子可以追踪，但是数论多少有点像时空，为此它也提供了一种寻找所有可能的路径方法和构建对所有可能路径的空间。从这种基本的对应中，金明迥提出了一种方案：寻找光的轨道以及探寻丢番图方程的有理解是同一个问题的两个方面.正如他在德国海德堡举行的数学物理会议上解释的那样。

 

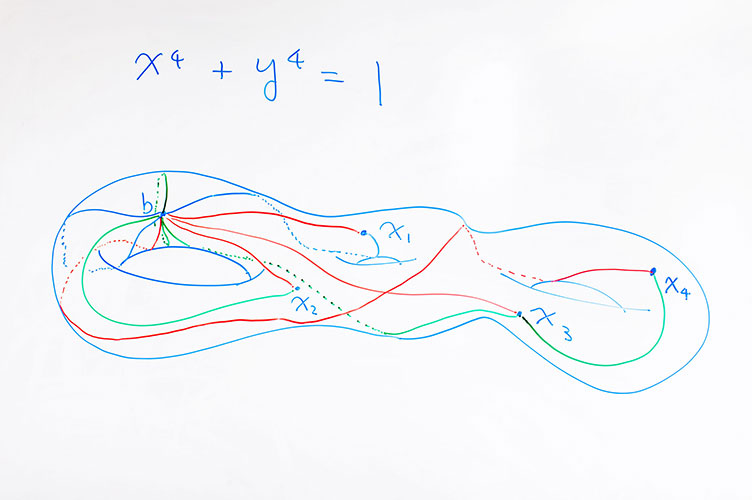
丢番图方程的解形成空间是由方程定义的曲线。这些曲线可以像圆一样是一维的（一维流形），或者他们可以是更高维的空间。例如，如果你试图寻找丢番图方程———x^4+y^4=1的复解，你就得到了一个三孔环面。在这个环面上的有理解缺乏几何结构，这样就很难去找到他们，但是它们可以被做成对应于具有结构的空间的更高维空间中的点。

金明迥通过考虑可以在环面上绘制环的方式（或等式定义的任何空间）来构造空间的高维空间。绘制环的过程如下：首先，选择一个基点，然后从该点绘制一个环到任何其他点，然后再返回。重复这个过程，画出连接基点和圆环面上其他点的路径。最后，你会有一个所有可能的环，他的起始点和结束点都在基点。这种环的集合是数学中一个重要的中心对象，它被称为空间的基本群。

 

​

 

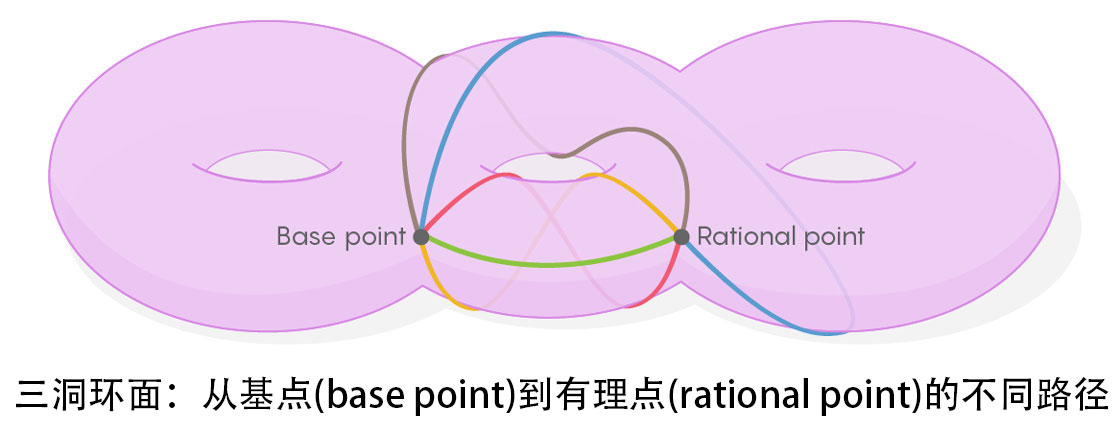
你可以使用在环面上的任何点作为你的基点。每一个点将有一个独一无二错综复杂的路径。每一个这些路径的集合可以被表示为一个点在一个更高维的“路径集合的空间”（就像所有的可能的三角形的空间）。这个空间的几何上非常类似于物理学家在规范场理论中构造的“空间空间”。当从一个点移动到环面上另一个点时，路径集合的变化非常类似于在实际空间中从一个点移动到另一个点时场变化的方式。

 

空间的空间具有额外的对称性，不表现于环面本身。虽然环面上的有理点之间没有对称性，但如果你进入所有路径集合的空间，就可以找到与有理点相关的点之间的对称性。这样你可以得到之前所看不见的对称性。

 

“我时常用到的一个短语是这些路径中有一种“隐藏的算术对称性”，高度类似于规范场论中内在的对称性”金明迥说。

 

 

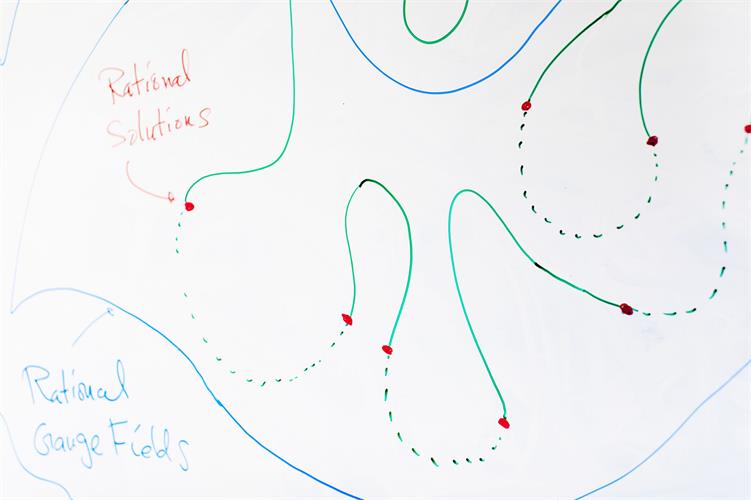
就像沙博蒂所说的那样，金明迥通过考虑在他所构造的更大的空间结构中交叉的点去寻找有理解，同时运用这个空间中的对称性去限制空间中的交叉点。他希望建立一个方程去精确的找到这些点。

在物理环境中，你可以想象光线可能会采取的所有可能的路径。这是你“所有路径的空间”。在这样的空间中，引起物理学家兴趣的是与时间最小化路径相对应的点。金明迥认为寻找有理点的过程与错综复杂的路径对应的点具有同样的性质——也就是说，当你开始思考丢番图方程的几何形式时，这些点将最小化某些性质。只是他还没有找出这种性质是什么。

“我开始寻找的东西是一个在数学环境中的最小作用量原理，他在邮件中写道。“我还是不太清楚，但我有信心，它就在那里，我能找到它。”

 

​

 

一个不确定的未来

 

在过去的几个月 ，我对几位数学家描述了金明迥由物理所启发的想法，他们都仰慕金明迥对数论的贡献。然而，当把金明迥遇到的困难传达给他们时，他们并不知道该如何下手。

 

“作为一个具有代表性的数论学家，如果你向我展示了金明迥一直在做的所有的这些“恐怖”的事情，并问我是否受到灵感启发，我会说'你到底在说什么鬼话？'”艾伦伯格如是说。

 

至今，金明迥并没有在他的论文中提及物理学。取而代之的是，他把他的目标称为Selmer簇,他考虑Selmer簇在所有Selmer簇空间中的关系。这些对于数论学者来说是可识别的术语。但是对于金明迥来说他们一直是物理学中某些物体的另一个名称。

 

“利用物理学中的思想去解决数论中的问题是有可能的，但是我还没有想好如何建立起这样的框架，”金明迥说，“我们在一个关键点上，对物理的理解足够成熟，以及有足够多的数论学者对这个问题感兴趣，所以接下来我们需要进一步推进。”

阻碍推进金明迥的方法一个困难在于在所有错综复杂的圈所组成的空间中寻找一些最小作用量的类型。在物理世界中，这样的观念十分自然，但是在算术中并不那么显然。甚至是对金明迥的工作了解最深的数学家，也非常关心他是否会找到它。

 

“我认为金明迥的工作将会给我们带来许多有价值的东西。我不认为我们要像金明迥想要的那样清晰的理解有理解所在的地方是某种算术规范场理论（arithmetic gauge theory）的经典解”哈佛大学数学物理教授阿尔纳夫·特里帕蒂说。

 

今天，物理学的语言几乎完全在数论的实践之外。金明迥认为这种情况肯定会改变。40年以前，物理和几何、拓扑的研究几乎都是独立。但在20世纪80年代，屈指可数的几位数学家和物理学家建立了有效的方法，该方法运用物理去研究形状的性质，现在这些学者都是领军人物了，而且该领域从未停止向前。

 

“如今不了解物理学几乎不可能对几何学和拓扑学感兴趣。我有理由确信在数论上也会有这种情况发生”在接下来的15年，金明迥说，“这样的联系将变得十分自然。”

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa