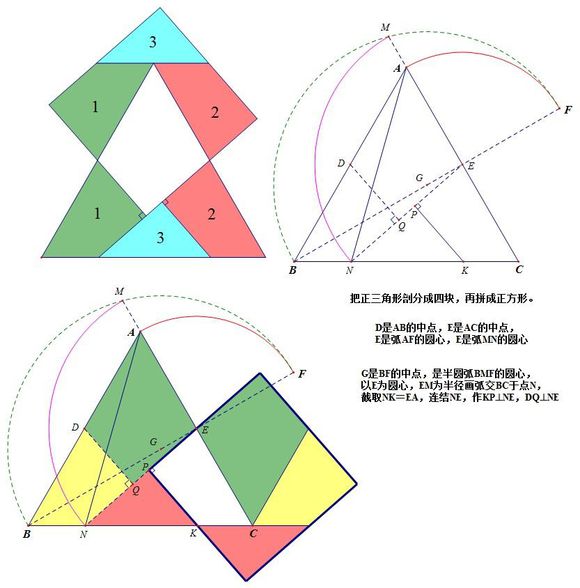
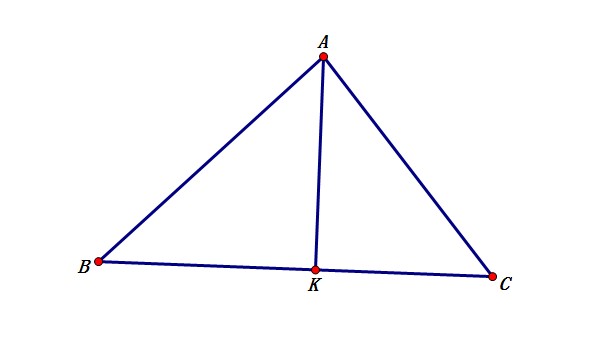
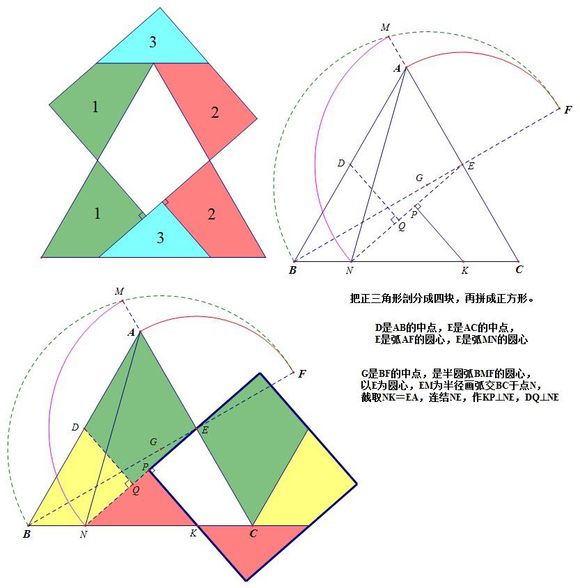
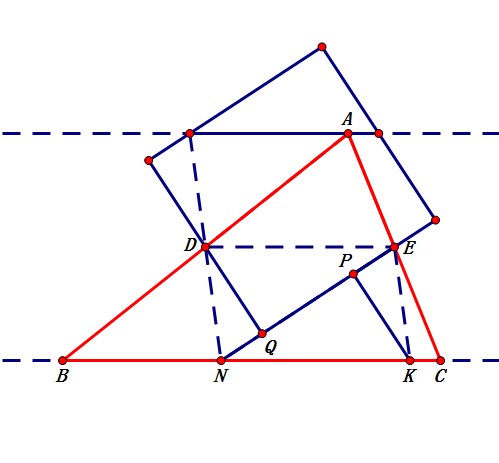
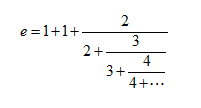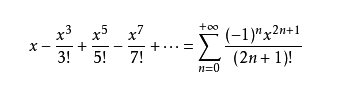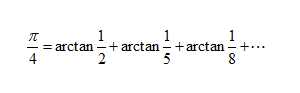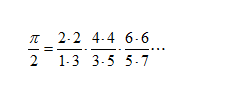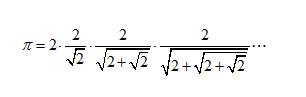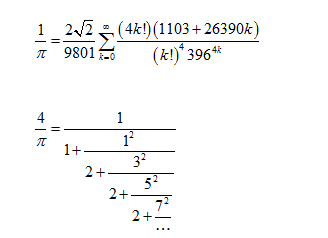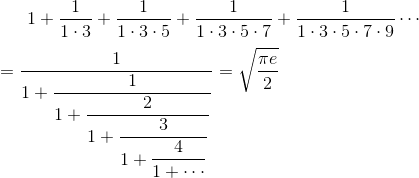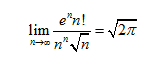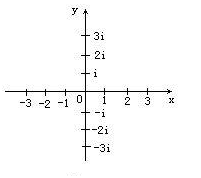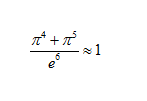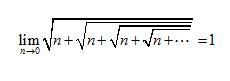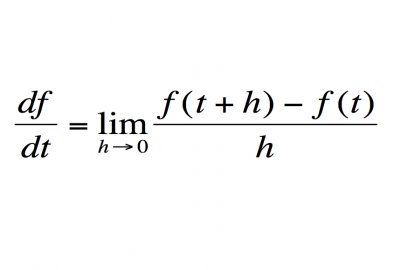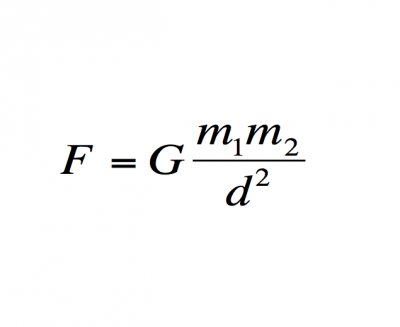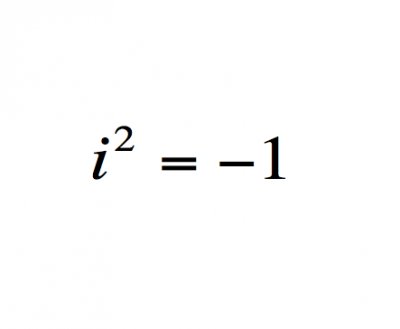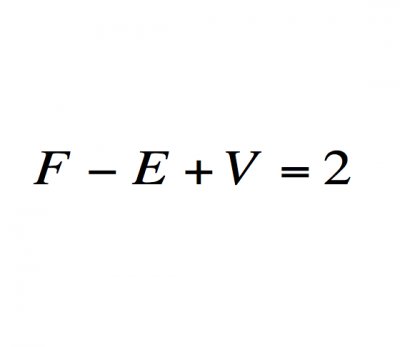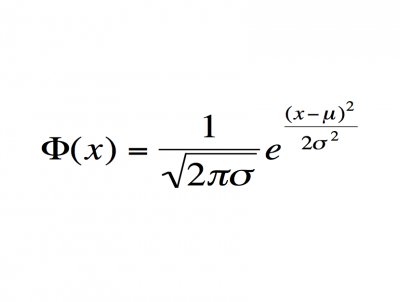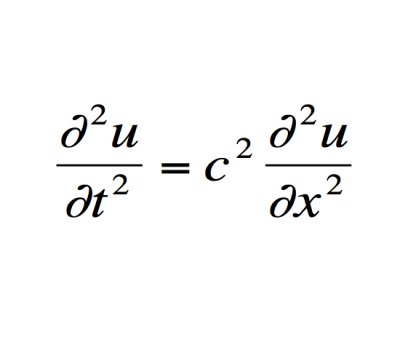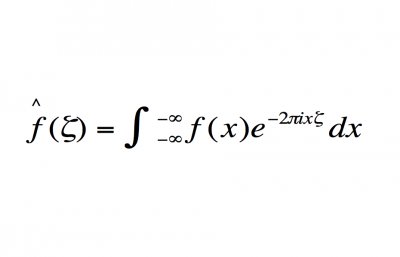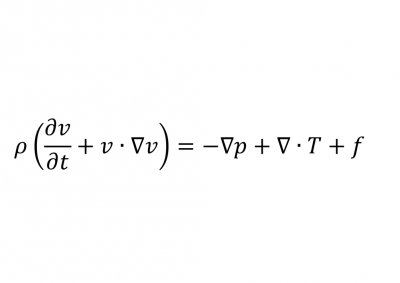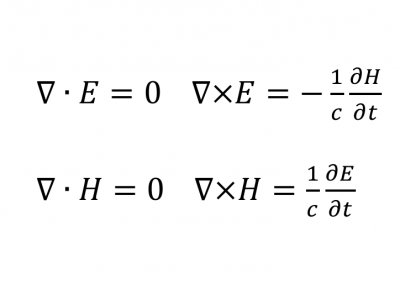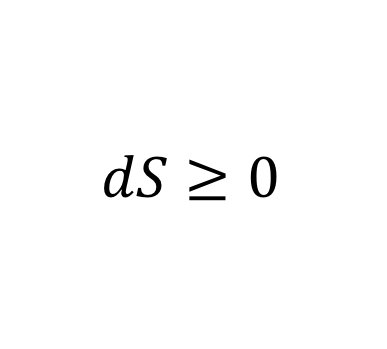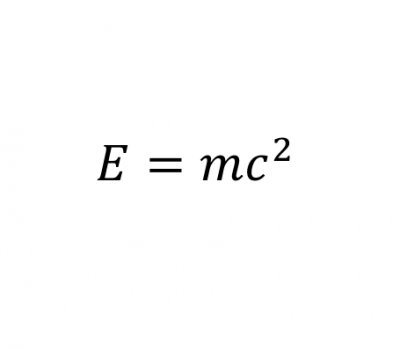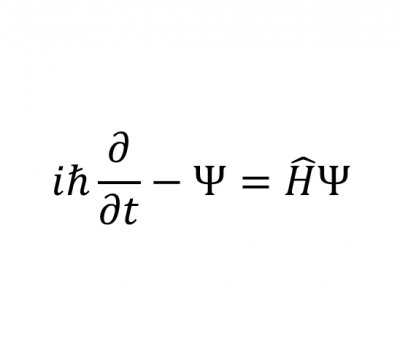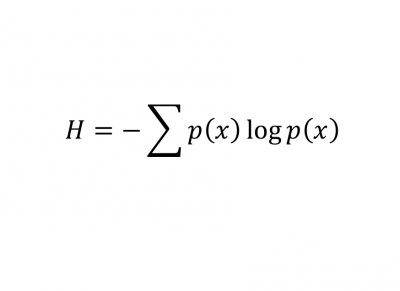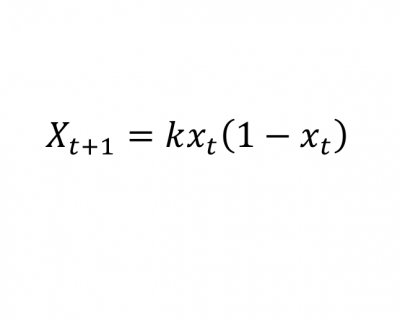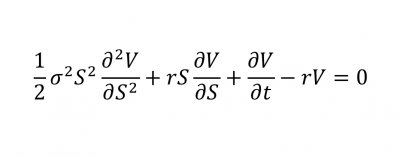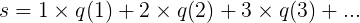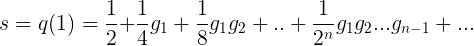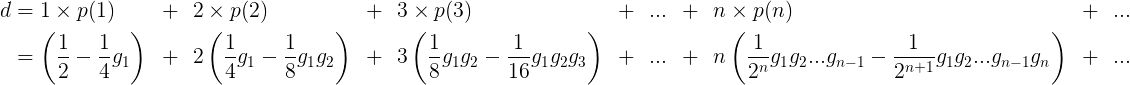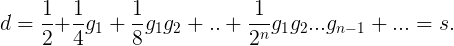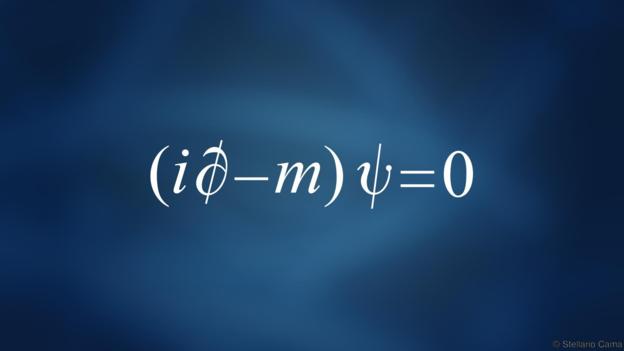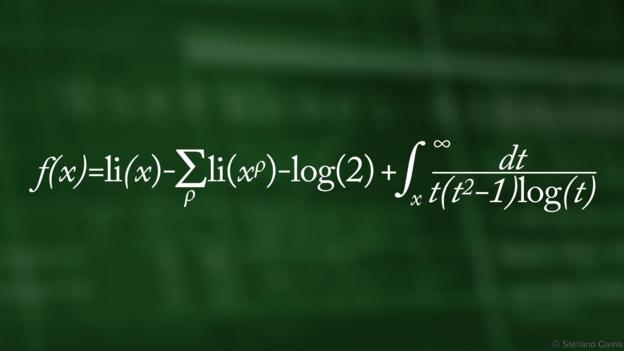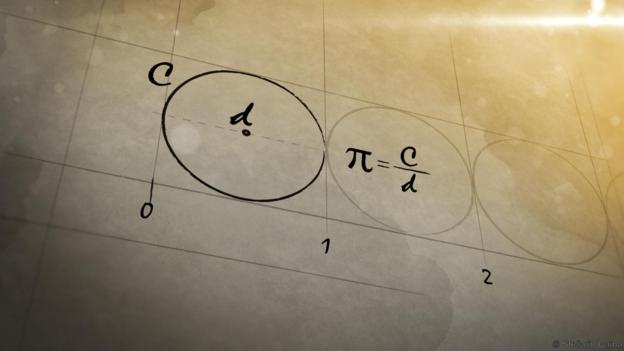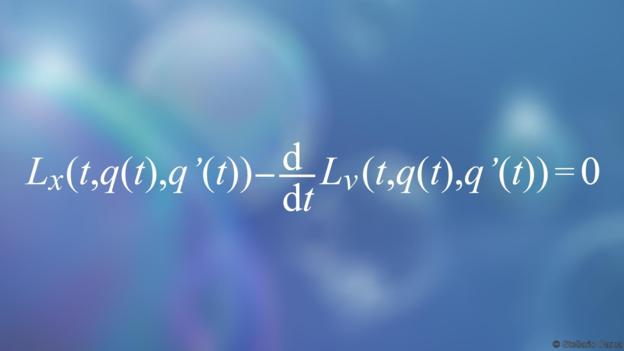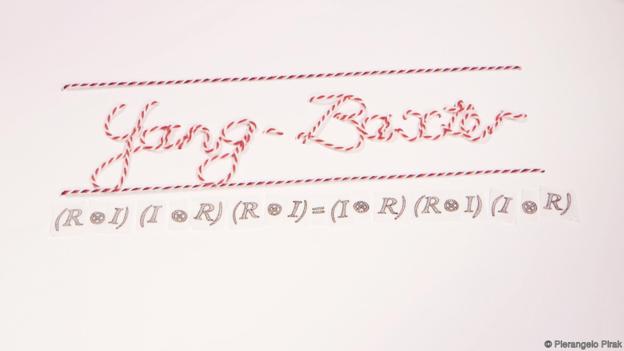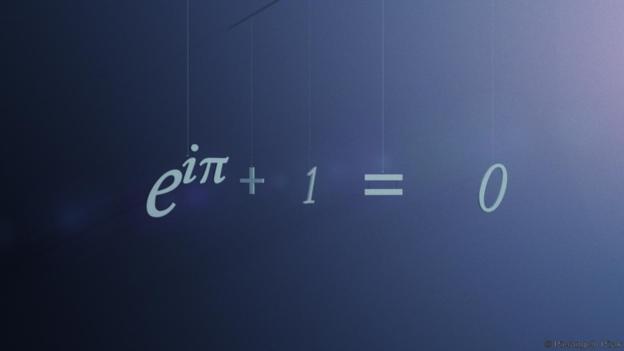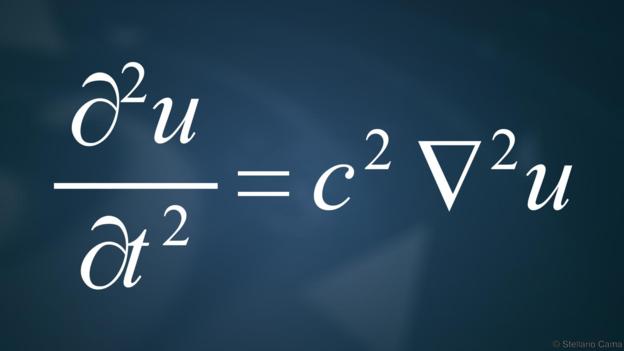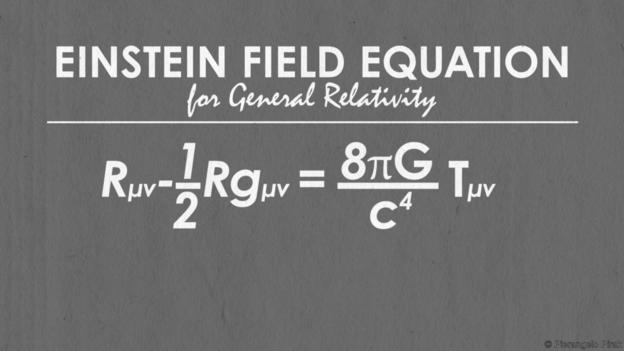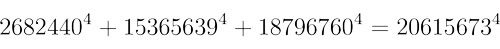计算它们?那只是数学海洋中的一滴水
作者:N_a_O_H_ , 哆嗒数学网群友, 常年活跃于数学贴吧。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
和朋友们聚餐吃饭,他们总会把最后验证账单的活交给我。我说我算不出来,还是按计算器吧。于是伴随着目瞪口呆,他们会惊诧地问我:“你不是数学系的吗?”
在诸多情况想,包括在研究中,这类体力活般的运算都交给了计算工具,比如说计算机。计算机,顾名思义,最初是人们发明出来代替人们进行计算工作的机器。随着编程语言被应用于计算机,人们可以精确定义给予计算机的指令,并且能以比人工计算快得多的速度得出结果,精确程度亦是令人信服。
人们利用计算机处理一个庞杂的计算任务时,依赖的是一种叫做循环结构的东西。这种结构把本身复杂的运算转化为一步一步的,每一步都依赖一个离散变量的小型计算,只需设定好想要的步数,就能令计算机按照这规定的步数进行一次次的机械的简单运算。就像织布机和流水线一样,这种简单机械的工作交给计算机是再适合不过的了,计算机运算的效率与准确程度都远高于人类。随着人们对数学的深入了解,指数函数,三角函数以及对数函数这些超越函数都可以通过这种循环结构计算了,而这些运算是初期的编程语言没有规定的。
泰勒公式是计算这些函数的一种方法,把上述函数转化为一个多项式,这些多项式每一项的系数也是有特定的规律的。这样,每一项的指数与系数都有规律可循,那么用循环结构执行就成为了可能。按照这种思路,就连定积分的计算也可以交给计算机了。
看上去很厉害,没错吧?
请仔细留意我上面的措辞。我说,计算机用泰勒公式去运算那一系列超越函数的函数值,这听起来似乎没有半点问题。然而泰勒公式是用一个多项式近似表示函数某点周围的性态,注意是近似!泰勒公式只是个有限项的多项式,只要你愿意你可以写出它的任意多项,但是它始终是有限项的。真正恒等于那些超越函数的是它们的泰勒级数,泰勒级数是一个无穷和。你用泰勒公式无论怎么精确,都只是泰勒级数的一个部分和,也就是其中有限项的和,其结果永远与精确值相差一些。
简单来说,得到上诉精确值或者近似值的方法,就是本文说的“数值计算”(这里打个引号,避免和真正专业的数值计算这个分支误会)。
计算机也可以计算定积分的数值,我们可以完全按照定积分定义相仿的思想来计算——取曲线下一列纵向的细长矩形面积之和来逼近曲线下的精确面积。这样的方法下,计算机无论如何努力,都只能把曲线下的面积化为有限个矩形之和,其结果自然与精确的结果有所偏差。当然,我们可以改进这些计算方法,比如把矩形改成梯形,或者利用根高级的理论简化步骤,但是我们得到的还是有限次计算得到的精确值或者近似值。
有人说,计算机进行了那么多次运算,其得出的结果的误差已经非常小了,以至于人们随时都能把它扔掉。不要着急,我完全没有要责难计算机计算能力的意思。我说了这么多,只是想说上述计算并没触及到数学的一个基础核心概念:无穷。
无穷这东西,其实并不像它们在实平面中那样离我们那么遥远,而是一直在我们身边。小学二年级引入了除法的概念,老师一再强调0永远不能作为除数。那时我想勤于思考的孩子都想过,那么0做除数会是什么后果呢,比如说1除以0?抱着好奇心他们把这个算式输进了计算器,得到的却是一个冷漠的Syntax Error,于是只好就此作罢。到了后来,随着知识的不断积累,学生们意识到了任何0之外的数除以0,得到的是无穷大,因为你无论有多少个0,它们的和就一定是0,所以结果只好是无穷大了。这种想法倒无可非议,只是流于想象,并不十分不严谨罢了。于是,“n/0”这类形式的无穷,大概就是我们最早能够接触到的了。
感谢数学家柯西和魏尔斯特拉斯,我们终于有了一种严谨的方式定义,证明和计算极限。那么我们回到上面的例子,我们还是来研究1/x在x=0处的极限。这次先让计算机来做。直接输入1/0会让电脑爆炸,所以我们只能通过一系列尽可能接近于1的数字来研究结果,1/0.1=10,1/0.01=100, 1/0.0001=10000, 1/0.00000001=100000000...千万不要以为这一系列结果告诉你很多东西,尤其是不能错误地就这几个结果,我们就臆断,x越接近于0,1/x越大,而这恰好是许多对数学不了解的人所犯的错误。数学中,对于有限的极限有这样一个性质:某处的极限存在(或者都趋于无穷),当且仅当每一个收敛到这点的数列,都收敛到一个相同值(或者都趋于无穷)。因此,为了用计算机证明这种极限,我们必须证明任意一个这样的数列都趋于正无穷,这将意味着我们必须验证无穷多个数列的结果,而且,就算我们能够验证无穷个序列的结果,那么对于这每个序列都有x趋于0时,y不断增大,注意我们能得出的只是不断增大这个事实,至于有多大呢?计算机暴力验证的办法,就行不通了。

来看另一方面,人们可以用极限的严格定义来证明,1/x在0处的值为无穷。容易验证对于任意给定的正整数N,存在0附近的某个点x,使得|1/x|>N。数学分析的知识告诉我们,1/x的绝对值可以比任何一个正整数都大,自然就是无穷大了。
从这里,我想引出这篇文章我真正想说的。我们数学系做数学的方式是用理性推理去证明数学问题的,这些数学命题很可能涉及无穷的概念。我们大多数人不会去纠结一个复杂的加减乘除运算式子,如何快速心算得到结果。比如,上面的命题“1/x在x=0处的极限为无穷”这一命题就是一个例子。暴力计算的思路很难验证一个涉及无穷的数学性命题,绝大多数情况下都只能验证有限个情况下命题的真伪性,而无法从本质上证明或证伪它。
下面我想再举另一个例子,这是我这周的C++课作业内容。作业要求编一个程序,来算采矿和淘金两种方法的收益,已知两种方法中,各有一定的概率获得一定数量的收入。要求设定一些随机变量,然后把程序跑1000000次,求平均数。这个作业的目的再明显不过了,无非是要验证数学实验的结果符合某个期望。作业中(具体的作业内容我不再叙述了)按照数学推理计算能得到数学期望的理论结果,采矿的期望收益为75美元,淘金为68美元。而用程序跑出来的结果,始终与这两个结果相差一些。诚然,如果你用程序模拟的结果最终成两个分别以75和68为中心的正态分布,或者能验证这个程序计算的次数越多(多于1000000次),结果越接近于75和68,那么自然是有说服力的。然而,尽管做出一个很大的样本,也不能从数学理论上认定,他们的数学期望就是75和68。如果要认定,两种情况都要求无限次的运算。而我们能通过有限次运算得出的,从某种意义上来讲是苍白无力的,看上去很接近75和68的结果根本不足以说明数学期望的存在性——无论他们怎么接近目标值。反过来说,倒是因为有了理论上数学期望的存在,多次运算后的结果一致地逼近某个数值,这样的一个结果才是可能的。我们熟知的投针实验和抛硬币实验都是一个道理。
这揭示了一个事实:在一些人认为很厉害的“数值计算”,在我们做数学的时候只是一个验证的工具,很多时候也许能给我们一些启发,但是大多时候一个数学理论突破的瓶颈跟计算机的这种计算没有半毛钱关系。甚至,我可以说严重一点,正如伟大哲学家康德也指出的,这些算式都是一个个经验性的命题,永远不会有真正的普遍性,从而没有指导意义。
这些“数值计算”够做到的,只是穷举和有限的运算,总而言之能做到的东西有限,不足以归纳证明带有任意性的命题,也就是本身蕴含着无穷的那些。实际上,计算机要做到真正的数学推理,需要换一种办法。这也是数学家们研究的一个领域,叫做机器证明。它的思路,已经不是“数值计算”去得到一些近似值,这个不是本文想讨论的范围。
在文章的最后,我想描述一下,有限在无限面前是多么渺小。
现在的计算机,如果要他完成一个需要2的500次方步骤才能完成计算,那简直是不可能完成的任务。但在,无穷面前,他可能只是一个很平常有限数,很多时候都可以忽略不计。比如,前面验证极限的时候,这个数字都出不了场呢!
说到底,这些“数值计算”可以覆盖的数学中的领域,标题上还高估了呢。所以,我是数学系的,但是是不会帮你们验证账单的。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

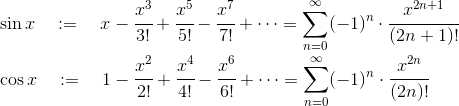


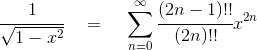
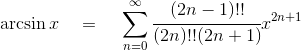
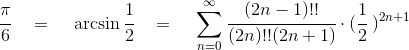









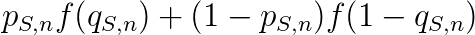
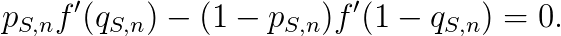



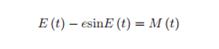 (1)
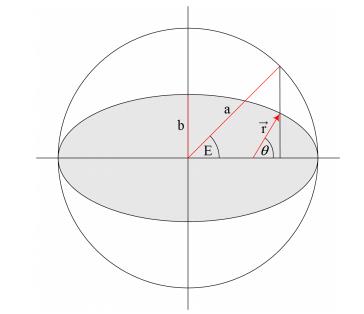
(1)
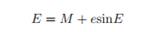 (2)
(2)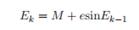 (3)
(3)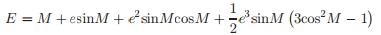 (4)
(4)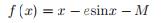 (5)
(5)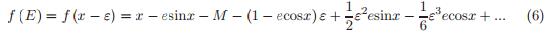
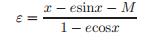 (7)
(7)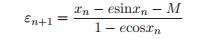 (8)
(8)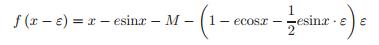 (9)
(9)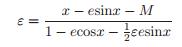 (10)
(10)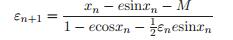 (11)
(11)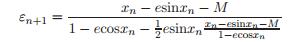 (12)
(12)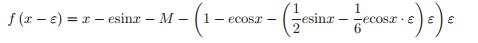 (13)
(13)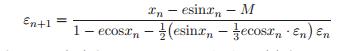 (14)
(14) 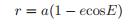 (15)
(15)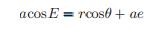 (16)
(16)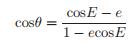 和
和 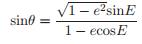 (17)
(17)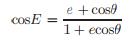 和
和 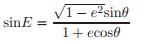 (18)
(18)