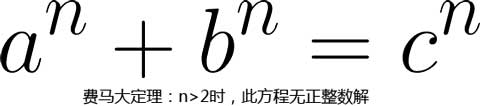关注微信:DuoDaaMath 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
作者,逆蝶,哆嗒数学网群友
数学中曾出现过许多的数学天才, 也有着众多的数学大师, 他们在数学方面的工作对数学的发展起着无可替代的作用. 众多的数学家在从事数学研究时也会有众多的研究成果, 这里不可能对所有的数学家都做个全面的介绍. 我们对其中的部分数学家进行一些简介, 然后把他们所研究过的级数方面的东西抽取出来, 来得到我们所想要的着重考虑的权, 以此来丰富权本身所包含的内容. 并且通过对格兰迪(Grandi)级数的权和计算, 来说明柯西(Cauchy)的收敛性要求似乎是太苛刻了, 而其他的权和是很有存在的必要的.
隐没的天才,阿贝尔(Able), 一个成就极高但是生前却没有得到认可的英年早逝的挪威天才数学家. 他完整给出了高于四次的一般代数方程没有一般形式的代数解的证明, 这曾经是一个悬疑达250多年的著名问题.
他和伽罗瓦(Galois)一样, 都是同一个时代最杰出的代数学家, 也都是由于柯西(Cauchy)的一时疏忽导致了英年早逝. 阿贝尔去世时26岁, 而伽罗瓦去世时年仅21岁. 阿贝尔也曾去拜访过大数学家高斯(Gauss), 但是高斯却看不上他, 将阿贝尔那写着划时代的伟大定理的六页手册扔在了一边.
阿贝尔在数学方面的成就是多方面的, 他研究过无穷级数以及幂级数, 使得他成为分析学严格化的推动者. 他还是椭圆函数论的奠基者, 他为椭圆函数论的研究开拓了道路,并深刻地影响着其他数学分支.
埃尔米特(Hermite)曾说:阿贝尔留下的思想可供数学家们工作150年.
阿贝尔在研究幂级数的时候, 曾证明了著名的阿贝尔第二定理. 我们抽取定理中的精髓, 可以得到关于发散级数的一种求和方法.
定义1(阿贝尔和) 设$\sum\limits_{n=0}^{\infty} a_n$产生的幂级数$\sum\limits_{n=0}^{\infty} a_nx^n$的收敛半径不小于1. 如果
\begin{align*} \lim\limits_{x\rightarrow 1^-} \sum\limits_{n=0}^{\infty} a_nx^n=s, \end{align*}
就称级数$\sum\limits_{n=0}^{\infty} a_n$在阿贝尔意义下收敛, 称$s$为级数的阿贝尔和.
在上一篇文章中我们定义了级数的权以及权和, 对于阿贝尔和, 相应的阿贝尔权为$\sum\limits_{n=0}^{\infty} x^n$, 以及权值为$\cfrac 1{1-x}$.
虽然我们曾指出, 一个规范的权一定是一个合理的权, 但还是对阿贝尔权的合理性作一些讨论(对将要介绍的另外几种权也有类似的结论). 其实由于讨论的是当$x\rightarrow 1^-$时的极限, 对我们有用的只是$x\ge 0$的部分, 所以可以默认为之后对阿贝尔权(也可将其简称为$s$权)的讨论都是对于$0\le x<1$而言的.
对固定的$x$, $\sum\limits_{n=0}^{\infty} a_nx^n$是级数$\sum\limits_{n=0}^{\infty} a_n$与级数$\sum\limits_{n=0}^{\infty} x^n$的直积, 也就是说这时候$b_n(x)=x^n$. 对于每个$a_n$, 其权均为不大于1的非负数, 并且满足$\lim\limits_{x\rightarrow 1^-} b_n(x)=\lim\limits_{x\rightarrow 1^-} x^n=1$, 所以Abel权是一个合理的权. 由于$\sum\limits_{n=0}^{\infty} x^n=\cfrac 1{1-x}$, 所以级数$\sum\limits_{n=0}^{\infty} a_n$的权值为$\cfrac 1{1-x}$, 当$x\rightarrow 1^-$时, 级数的权值趋于$\infty$, 这些都是一些显而易见的事实.
对于柯西权, 切萨罗权, T权以及$\mu$权, 也都有$0\le b_n(x)\le 1$, 并且级数的权值趋于$\infty$. 今后我们讨论的权也多数都具有这种性质, 但也不排除有例外的情形. 可以看出, 阿贝尔权的加权方式是通过弱化级数比较靠后的项对级数整体的影响, 然后再通过取极限的方式把每一项的比重都加上去, 我们之后讨论的其他类型的权大多也都是这样的.
现在来计算格兰迪级数的阿贝尔和. 根据$\sum\limits_{n=0}^{\infty} (-1)^n$与阿贝尔权$\sum\limits_{n=0}^{\infty} x^n$的直积
\begin{align*} \sum\limits_{n=0}^{\infty} (-1)^nx^n=\cfrac 1{1+x} \end{align*}
可得$s=\lim\limits_{x\rightarrow 1^-} \cfrac 1{1+x}=\cfrac 12$, 即格兰迪级数的阿贝尔和为$\cfrac 12$. 这样格兰迪级数的和应该是$\cfrac 12$的观点又得到了进一步的支持.
阿贝尔权与切萨罗权的权指标变化范围不同, 取极限的方式也不同, 但是这两种看似并没有任何关系的权却可以通过等式
\begin{align*} \sum\limits_{n=0}^{\infty} a_nx^n=(1-x)^2\sum\limits_{n=0}^{\infty} (n+1)\sigma_nx^n \end{align*}
联系起来, 并且有下述结论.
定理1 如果级数$\sum\limits_{n=0}^{\infty} a_n$的切萨罗和为$\sigma$, 那么其阿贝尔和存在且与切萨罗和相等.
现在我们有切萨罗和存在的级数其阿贝尔和一定存在且相等, 那么是否有阿贝尔和存在但切萨罗和不存在的级数呢?易见交错整数级数$\sum\limits_{n=0}^{\infty} (-1)^n(n+1)$的切萨罗和不存在, 但其阿贝尔和为$\cfrac 14$, 所以可以把阿贝尔权看成切萨罗权的一种严格推广.
之前曾得到了如果$a_n=o(\cfrac 1n)$, 那么切萨罗和存在可以推出柯西和存在且相等. 其实对于阿贝尔权, 也有相应的类似结论.
定理2(Tauber)
设幂级数$\sum\limits_{n=0}^{\infty} a_nx^n$具有阿贝尔和$s$. 如果$a_n=o(\cfrac 1n)$, 那么其柯西和存在且与阿贝尔和相等.
我们在此指出, 其实就如切萨罗和一样, 有着比$a_n=o(\cfrac 1n)$更强的结论. 在阿贝尔和存在的情况下, 只要
\begin{align*} \cfrac {\sum\limits_{k=0}^n ka_k}n\rightarrow 0, n\rightarrow\infty \end{align*}
就有级数的柯西和存在, 且两者相等. 而且更进一步的还有, 在阿贝尔存在的前提下, $\cfrac {\sum\limits_{k=0}^n ka_k}n\rightarrow 0(n\rightarrow\infty)$ 其实是柯西和存在并且等于阿贝尔和的充要条件. 根据对切萨罗和与阿贝尔和的讨论可以发现, 似乎
\begin{align*} \cfrac {\sum\limits_{k=0}^n ka_k}n \end{align*}
是个很特殊的数列.
我们下面再讨论一些有趣的东西, 以此暂时结束对阿贝尔权的介绍, 但是涉及到了些许复变函数论的知识:
诸如格兰迪级数与交错级数
\begin{align*} \sum\limits_{n=0}^{\infty} (-1)^n\qquad\sum\limits_{n=0}^{\infty} (-1)^n(n+1) \end{align*}
与阿贝尔权的直积是
\begin{align*} \sum\limits_{n=0}^{\infty} (-1)^nx^n\qquad\sum\limits_{n=0}^{\infty} (-1)^n(n+1)x^n \end{align*}
其和函数$s(x)$分别是
\begin{align*} \cfrac 1{1+x}\qquad\cfrac 1{(1+x)^2} \end{align*}
和函数的定义域都是$(-\infty,-1)\cup (-1, +\infty)$, 比区间$(-1, 1)$大的多, 特别地$x=1$在其定义域内. 那么是否可以把阿贝尔和中的极限$x\rightarrow 1^-$改成直接将$x=1$带入其和函数呢?换句话说, 阿贝尔和$s$是否就是$s(1)$?
事实上这是不可以的, 我们将用两个函数对其作出说明.
(1)
\begin{align*} f(z)=e^{-\frac 1{(1-z)^2}}. \end{align*}
$z=1$是这个函数唯一的奇点且是本性奇点, 所以我们是无法定义$f(z)$在$z=1$处的函数值使其在$z=1$处连续的.
由于$f(z)$在单位圆盘内解析, 所以可以在$|z|<1$时展开成幂级数
\begin{align*} f(z)=\sum\limits_{n=0}^{\infty} c_nz^z. \end{align*}
又因为$z$取实数时, $f(z)$也取实数值, 所以$c_n$均是实数.
考虑级数$\sum\limits_{n=0}^{\infty} c_n$, 其与阿贝尔权的直积$\sum\limits_{n=0}^{\infty} c_nx^n$的和函数
\begin{align*} s(x)=f(x)=e^{-\frac 1{(1-x)^2}}. \end{align*}
但是由于$f(1)$的值无法适当定义, 所以s(1)并不存在. 但是这并不足以说明问题, 因为对于$s(x)$我们主要还是考虑$x$取实值的情况,这时可以定义:
\begin{align*} s(x)=\begin{cases} e^{-\frac 1{(1-x)^2}}, & x\neq 1;\\ 0, & x=1. \end{cases} \end{align*}
于是$s(x)$不仅在$x=1$处连续, 而且还是一个$C^{\infty}(R)$ 函数.
(2)
\begin{align*} f(z)=e^{\frac {z+1}{z-1}}. \end{align*}
$z=1$是这个函数的唯一的奇点且是本性奇点, 所以同样无法定义$f(z)$在$z=1$处的函数值使其在$z=1$处连续.
先不考虑将要讨论的$s(1)$值问题, 我们来探讨一下这个函数本身具有什么性质:
$f(z)$在单位圆盘内部有界, 也就是当$|z|<1$时, $|f(z)|<1$; 而当$|z|=1$但$z\neq 1$时, $|f(z)|=1$.
当$z$沿着圆内的任意一条直线段趋于1时, 均有$f(z)$趋于0;
当$z$沿着圆外的任意一条不是单位圆的切线的直线段趋于1时, 均有$f(z)$趋于$\infty$;
当$z$沿着单位圆周趋于1时, $f(z)$趋于1;
但是当$z$沿着单位圆的切线趋于1时, $f(z)$却并不存在极限值.
由于这个函数具有这些如此奇妙的性质, 所以在复变函数论中举反例的时候回经常用到它.
现在回归主题, 我们有与之前(1)中的函数完全类似的结论. 由于$f(z)$在单位圆盘内解析, 所以可以在$|z|<1$时展开成幂级数$f(z)=\sum\limits_{n=0}^{\infty} c_nz^z$. 由于$z$取实数时, $f(z)$也取实数值, 所以$c_n$均是实数.
考虑级数$\sum\limits_{n=0}^{\infty} c_n$, 其与阿贝尔权的直积$\sum\limits_{n=0}^{\infty} c_nx^n$的和函数
\begin{align*} s(x)=f(x)=e^{\frac {x+1}{x-1}}. \end{align*}
但是由于$f(1)$的值无法适当定义, 所以$s(1)$并不存在. 那抛弃$f(z)$, 只考虑$s(x)$, 能不能恰当的定义$s(1)$的值呢?
由于
$ \lim\limits_{x\rightarrow 1^-} s(x)=0, \lim\limits_{x\rightarrow 1^+} s(x)=\infty,\\ $
所以我们无法像(1)中的函数那样适当的定义$s(1)$的值, 也就是说并不能把$s=\lim\limits_{x\rightarrow 1^-} s(x)$简单的用$s=s(1)$来替代.
阿贝尔权还可以推广到更一般的非整幂情形, 但是没有阿贝尔权常用, 而且非整幂的情形还可由狄利克雷(Dirichlet)权得到, 有兴趣的读者可以单独探究一下非整幂权的性质.
另外还需指出泊松(Poisson)利用阿贝尔和处理发散的三角级数得到了很重要的单位圆盘上的泊松核, 然而他本人却并不知道他用的实际上就是发散级数的阿贝尔和. 之后我们也会对三角级数作一些简要的讨论.
无限猴子定理:有无限只猴子用无限的时间会产生特定的文章. 其实不必要出现了两件无限的事物, 一只猴子打字无限次已经足够打出任何文章, 而无限只猴子则能即时产生所有可能的文章.
无限猴子定理是来自博雷尔(Borel)一本谈概率的书籍中, 这个定理是概率论中的柯尔莫哥洛夫的零一律的其中一个命题的例子. 博雷尔是著名的法国数学家, 对现代数学的许多分支都产生了深刻的影响. 他引进测度的概念之后, 他的学生勒贝格(Lebesgue)将他的测度论推向一般化, 并定义了勒贝格积分, 引起了一场积分学的革命.
有限覆盖是博雷尔最为人熟知的定理, 但是博雷尔对数学的贡献当然远不止于此. 他也曾研究过无穷级数, 并且定义了一种和, 我们不妨称之为博雷尔和.
下面我们借由阿贝尔权的变形, 通过类似于之前引入$\mu$权的方法, 来引入一种$u$权, 并从$u$权导出博雷尔权.
对阿贝尔权变形:
\begin{align*} s(x)=\sum\limits_{n=0}^{\infty} a_n=(1-x)\sum\limits_{n=0}^{\infty} S_nx^n=\cfrac {\sum\limits_{n=0}^{\infty} S_nx^n}{\sum\limits_{n=0}^{\infty} x^n}. \end{align*}
注意到分子上$S_n$的系数之和恰好等于分母, 这启发我们可以类似于定义$\mu$权一样来定义$u$权.
定义2(u权)设有级数$\sum\limits_{n=0}^{\infty} a_n$, 另外有函数项级数$\sum\limits_{n=0}^{\infty} b_n(x)$满足$b_0(x)>0, b_n(x)\ge 0$.
如果有
\begin{align*} \lim\limits_{x\rightarrow\infty}\cfrac {u_n(x)}{\sum\limits_{k=0}^{\infty} u_k(x)}=0,\quad\lim\limits_{n\rightarrow\infty}\cfrac {u_n(x)}{\sum\limits_{k=0}^{\infty} u_k(x)}=0. \end{align*}
那么由
\begin{align*} u(x)=\cfrac {\sum\limits_{n=0}^{\infty} S_nu_n(x)}{\sum\limits_{n=0}^{\infty} u_n(x)} \end{align*}
所得到的权称为$u$权. 如果
\begin{align*} \lim\limits_{x\rightarrow\infty} u(x)=S, \end{align*} 就称级数$\sum\limits_{n=0}^{\infty} a_n$依$u$权收敛, $S$称为级数的$u$和.
我们可以赋予$u(x)$一些具体的函数, 从而得到具体的$u$权. 通过取定$u(x)$, 就可以得到之前所提到的博雷尔权.
定义3(博雷尔和) 取$u$权中的$u_n(x)=\cfrac {x^n}{n!}(x\ge 0)$, 此时$u(x)$化为 \begin{align*} u(x)=\cfrac {\sum\limits_{n=0}^{\infty} S_n\cfrac {x^n}{n!}}{\sum\limits_{n=0}^{\infty} \cfrac {x^n}{n!}}=e^{-x}\sum\limits_{n=0}^{\infty} S_n\cfrac {x^n}{n!}. \end{align*} 如果 \begin{align*} \lim\limits_{x\rightarrow\infty} u(x)=S, \end{align*} 就称级数$\sum\limits_{n=0}^{\infty} a_n$依博雷尔收敛, 称$S$为级数的博雷尔和.
我们来看一看格兰迪级数的博雷尔和是多少. 根据 \begin{align*} \sum\limits_{n=0}^{\infty} \cfrac {x^{2n}}{2n!}=\cfrac {e^x+e^{-x}}2 \end{align*} 可以得到 \begin{align*} u(x)=\cfrac 12+\cfrac 12e^{-2x}. \end{align*} 于是就有格兰迪级数的博雷尔和是$\cfrac 12$, 这样就又支持了格兰迪级数的和应该是$\cfrac 12$的观点. 应当注意对于一般的$u$权来说, 格兰迪级数的$u$和并不一定总是存在.
堪与高斯媲美的年轻人,黎曼(Riemann), 一个比数学王子高斯小五十岁的年轻人, 却能得到高斯的高度评价. 因为高斯的成就很高, 所以高斯对别人的赞赏也就一向极为吝啬, 黎曼能够获得高斯的赏识, 这对于高斯来说也是很罕见的.
黎曼是19世纪最富有创造性的德国数学家, 其作品以不拘小节著称, 经常对一些结论略而不证. 而在他看来一些显而易见的结论却常常要经历数十年之后才能为后人所证明. 黎曼还有一个非常著名的直到现在仍未被解决的猜想, 谓之“黎曼猜想”, 被收录于希尔伯特(Hilbert)第八问题之中.
曾经有人问希尔伯特:如果你能在五百年后重返人间,你说的第一句话会是什么?他回答说:是否已经有人解决了黎曼猜想?
黎曼还提出了十分重要的黎曼几何, 为广义相对论所描述的空间提供了理论框架. 爱因斯坦曾经写道:惟有黎曼这个孤独而不被世人了解的天才,在上个世纪中叶便发现了空间的新概念———空间不再一成不变,空间参与物理事件的可能性才开始显现.
黎曼曾提出一种求和方法, 可以用它来证明傅里叶级数展开的唯一性. 接下来我们来关注这种和式, 进而得到$R$权.
定义4($R$和)设有级数$\sum\limits_{n=0}^{\infty} a_n$, 记
$ R(h)=a_0+\sum\limits_{n=1}^{\infty} a_n(\cfrac {\text{sin}nh}{nh})^2=a_0+a_1(\cfrac {\text{sin}h}{h})^2+a_2(\cfrac {\text{sin}2h}{2h})^2+\cdots. $
如果
$ \lim\limits_{h\rightarrow 0} R(h)=R, $ 就称级数$\sum\limits_{n=0}^{\infty} a_n$在黎曼意义下收敛, $R$称为级数的黎曼和.
注:为了与微积分里面的黎曼和区分, 我们今后称上述收敛为$R$权收敛, 称其和为$R$和. 另外我们指出, $R$权即是$1+\sum\limits_{n=1}^{\infty} (\cfrac {\sin nh}{nh})^2$.
通过借助于多重对数函数$\text{Li}_s(z)=\sum\limits_{n=1}^{\infty} \cfrac {z^n}{n^s}=z+\cfrac {z^2}{2^s}+\cfrac {z^3}{3^s}+\cdots$ 可以证明格兰迪级数的$R$和也是$\cfrac 12$, 这又说明了似乎格兰迪级数的和更应该$\cfrac 12$而不是把它当成一个发散的级数看待.
另外也有与$R$权很相似的权, 譬如 $ \sum\limits_{n=1}^{\infty} \cfrac {\text{sin}^2nh}{n^2h}, $ 应当注意它不是一个合理的权, 从而也不是一个规范的权. 但是却有这样的结论:
如果级数$\sum\limits_{n=0}^{\infty} a_n$的一般项趋于0, 即$\lim\limits_{n\rightarrow\infty} a_n=0$,那么 $ \lim\limits_{h\rightarrow 0} \sum\limits_{n=1}^{\infty} a_n\cfrac {\text{sin}^2nh}{n^2h}=0. $ 由于其不是一个合理的权, 所以我们就不去深究它了(这里的求和是从$n=1$开始的).
关于$R$权, 可以将其推广为: $ 1+\sum\limits_{n=1}^{\infty} (\cfrac {\text{sin}nh}{nh})^k\quad (k>1) $ 这种更一般的权, 这里要求$k>1$是为了让其是一个规范的权. 但是读者可能会问, 当k是奇数时, $(\cfrac {\text{sin}nh}{nh})^k$有可能是负的, 而当k不是整数时, $(\cfrac {\text{sin}nh}{nh})^k$也有可能不是个实数或者说会成为复数, 那是不是加上绝对值, 使用一般项为$|\cfrac {\text{sin}nh}{nh}|^k$的权更好呢?
其实我们之前没有要求过权的一般项不能是负数, 也没曾说过一般项不能是复数, 对于$1+\sum\limits_{n=1}^{\infty} (\cfrac {\text{sin}nh}{nh})^k$这种权我们有多重对数函数作为工具, 而加上绝对值之后几乎什么事情都做不了, 所以通常并不对其加上绝对值.
无法画出图像的函数: $D(x)=\lim\limits_{k\rightarrow\infty}(\lim\limits_{j\rightarrow\infty} (\cos (k!\pi x)^{2j}))$.
$D(x)$即是在有理点取1无理点取0的著名的狄利克雷(Dirichlet)函数. 在柯西之前, 数学家对于函数的连续性都有着不同的看法, 其中有一种说法是可以用初等函数通过某种形式表示出来的函数在大部分点都是连续的. 然而狄利克雷函数是一个处处不连续的函数, 但是却可以用初等函数以及极限的手段表示出来.
狄利克雷,德国数学家, 解析数论的奠基者, 在数学领域中的多个分支都做出了很有影响力的成果. 他的首篇论文即是费马大定理在$n=5$时的证明, 后来亦证明了$n=14$的情况. 通过利用他在研究解析数论时构造的极其重要的狄利克雷级数, 来得到我们所需要的狄利克雷权, 而且这将是这一段落引入的最后一种具体形式的权.
定义5(狄利克雷和) 设$0\le \lambda_0<\lambda_1<\lambda_2<\cdots$ 且$\lambda_n$趋于$\infty$, 那么对于级数$\sum\limits_{n=0}^{\infty} a_n$, 如果 $ \lim\limits_{s\rightarrow 0^+}\sum\limits_{n=0}^{\infty} a_ne^{-\lambda_ns}=\lambda, $ 就称级数$\sum\limits_{n=0}^{\infty} a_n$在狄利克雷意义下收敛, $\lambda$称为级数的狄利克雷和, 并且相应的我们有狄利克雷权$\sum\limits_{n=0}^{\infty} e^{-\lambda_ns}$.
不难发现, 阿贝尔权可以通过换元以及适当选取$\lambda_n$作为狄利克雷权的特殊情形, 对于非整幂的情况也有类似的结论, 所以狄利克雷权本身就是包含着很多权的权族. 我们考虑格兰迪级数的狄利克雷和, 但是就如$\mu$权一样, 由于狄利克雷权本身是一个包含很多种权的权族, 所以格兰迪级数的狄利克雷和并不一定存在(之后我们会指出反例). 退而求其次, 我们考虑狄利克雷权的一种特殊情形, 其在解析数论中具有重要的应用.
定义6($\zeta$和) 取狄利克雷权中的$\lambda_n$为 \begin{align*} \lambda_n=\begin{cases} 0, & n=0;\\ lnn, & n\ge 1. \end{cases} \end{align*} 此时$\sum\limits_{n=0}^{\infty} a_ne^{-\lambda_ns}$化为 $ a_0+\sum\limits_{n=1}^{\infty} \cfrac {a_n}{n^s}. $ 如果 $ \lim\limits_{s\rightarrow 0^+}\sum\limits_{n=0}^{\infty} \cfrac {a_n}{n^s}=\lambda, $ 就称级数$\sum\limits_{n=0}^{\infty} a_n$在$\zeta$意义下收敛, $\lambda$称为级数的$\zeta$和, 相应的有$\zeta$权$\sum\limits_{n=0}^{\infty} \cfrac 1{n^s}$.
注:借由黎曼$\zeta$函数($\zeta(z)=\sum\limits_{n=1}^{\infty} \cfrac 1{n^s}=\cfrac 1{1^s}+\cfrac 1{2^s}+\cfrac 1{3^s}+\cfrac 1{4^s}+\cdots$)的知识可以证明格兰迪级数的$\zeta$和为$\cfrac 12$, 这里称这种求和方式为$\zeta$也是因为当取$a_0=0, a_n=1(n\ge 1)$时的函数恰好为黎曼$\zeta$函数.
介绍完我们常用的几种权之后, 现在给出权规范性的判别法, 并利用此判别法对之前所介绍的几种权的规范性作一个简单验证.
定理3(判别法) 设有权$\{\sum\limits_{n=0}^{\infty} b_n(x)|x\in X\}$. 如果它是合理的, 并且存在常数$M$使得 $ \sum\limits_{n=0}^{\infty} |b_n(x)-b_{n+1}(x)|\le M\quad(\forall x\in X) $ 另外如果对任意的$x\in X$, 还有$\lim\limits_{n\rightarrow\infty} b_n(x)=0$成立. 那么$\{\sum\limits_{n=0}^{\infty} b_n(x)|x\in X\}$是一个规范权.
有了判别法之后, 我们可以对我们之前讨论过的权作一个验证.
柯西权, 切萨罗权, $T$权, $\mu$权: 合理性均不难验证. 由于权族中的每个级数的通项都是从1递减到0的, 所以可取$M=1$. 又因为权族中的每个级数只有有限项不为0, 所以$\lim\limits_{n\rightarrow\infty} b_n^{(m)}=0$是满足的, 因此是规范的.
阿贝尔权: 由$\lim\limits_{x\rightarrow 1^-} x^n=1$可得其合理性. 如果把$x$的取值范围$X$取为$(-1, 1)$, 那么$M$是不存在的, 所以我们需要把$X$取为$[0,1)$, 这时我们就可以取$M=1$. 另外$\lim\limits_{n\rightarrow\infty} x^n=0$也是显然成立的. 所以是规范的.
注:从阿贝尔权的例子可以看出,在考虑权收敛的时候适当的选取权指标的取值范围也是必要的.
$u$权: 根据$\lim\limits_{x\rightarrow\infty}\cfrac {u_n(x)}{\sum\limits_{k=0}^{\infty} u_k(x)}=0$易见其合理性. 另外显然可以取$M=2$. 最后一个条件即是$\lim\limits_{n\rightarrow\infty}\cfrac {u_n(x)}{\sum\limits_{k=0}^{\infty} u_k(x)}=0$. 由于博雷尔权也是$u$权的一种, 所以也是规范的.
$R$权: 由$\lim\limits_{h\rightarrow 0} (\cfrac {\text{sin}nh}{nh})^2$=1可得其合理性. 对于$R$权的$M$的存在性并不是像其他几种权那样显而易见, 我们只指出可取$M=\int_0^{\infty}|\cfrac d{dx}(\cfrac {\text{sin}x}x)^2|dx$. 最后一个条件$\lim\limits_{n\rightarrow\infty} (\cfrac {\text{sin}nh}{nh})^2=0$也是成立的, 于是得其规范性.
狄利克雷权: 由$\lim\limits_{s\rightarrow 0+} e^{-\lambda_ns}=0$得到合理性. 可取$M=1$, 以及根据$\lim\limits_{n\rightarrow\infty} \lambda_n=\infty$有$\lim\limits_{n\rightarrow\infty} e^{-\lambda_ns}=0$, 由此即得其规范性. 于是$\zeta$权也是规范的.
我们在这里着重对几种特殊的权及权和作一些介绍, 看似所有的求和方式都是权和, 但事实上却确实也存在着非权和的一些很重要的求和方式, 我们之后会举出具体的例子.
下一节我们将会特别考虑一些发散级数的计算问题, 例如所有正整数的和为$1+2+3+\cdots+n+\cdots=-\cfrac 1{12}$等有趣结果.
关注微信:DuoDaaMath 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa