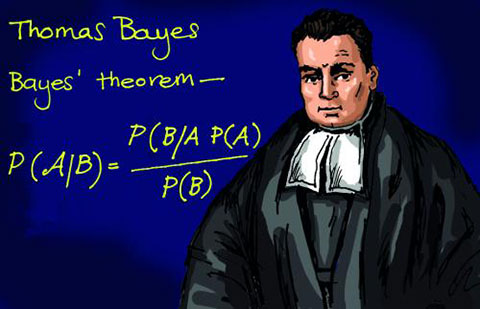关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

美国当地时间2月22日（北京时间2月23日），第87届奥斯卡获奖名单全部出炉。 《鸟人》成为最大赢家，获得最佳影片、最佳导演、最佳摄影、最佳原创剧本四项大奖。 讲述数学家图灵故事的电影《模仿游戏》获得最佳改编剧本奖。 而剧中图灵的扮演者“卷福”本尼迪克特·康伯巴奇在影帝的角逐中输给了《万物理论》霍金的扮演者“小雀斑”埃迪·雷德梅恩，被网友戏称“图灵”败给了“霍金”。

 

 

《模仿游戏》改编自安德鲁·霍奇斯编著的传记《艾伦·图灵传》，讲述“计算机科学之父”艾伦·图灵的传奇人生，故事主要聚焦于图灵在二战期间协助盟军破译德国密码系统“恩格玛”的经历。影片中图灵和他的团队经历无数挫折与失败，终于发明了密码破解装置——克里斯托弗，成功破译史上最难解的“谜”，拯救了二战中至少1400万人的生命。然而战后，英国政府却发现了他最深不可告人的秘密——他是一个同性恋。图灵因此被判有罪，被“化学阉割”。

 

​

 

这部影片中，“图灵机”以及“图灵测试”这些数学或者计算机科学的专业名词也得到了艺术化的演绎，让人知道了这位伟大数学家的其他学术成就。

 

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

素数又叫做质数，小学生都知道是什么意思。如果这位小学生对于数学的课外阅读还不错的话，很容易就能证明素数是无限的。

那么，这篇文章岂不是很水？再讲一个小学里总所周知的事？我们哆嗒数学网小编的回答：“是，也不是！”，我们的确在讨论一个简单的数学结论，但却在用不同的数学方法。方法可能涉及抽象代数、拓扑学以及集合论这种大学生都不一定会学习的方法。

文章受到《GÖDEL’S LOST LETTER AND P=NP》博客中文章的启发（WordPress上的博客，一般打不开），想和大家一起分享。

大学生看不懂的高级方法？这么任性？——不是任性，只是忍不住。

第一个方法，从简单的开始讲。小学生能看懂的就是欧几里得的在2000多年前提供的办法了。

假设只有有有限多个素数。设$p_1,p_2,\cdots,p_m$是全部$m$个素数，令$p=p_1p_2\cdots p_m+1$。则$p_1,p_2,\cdots,p_m$都不是$p$的素因数。所以$p$是有一个与$p_1,p_2,\cdots,p_m$都不同的素数。矛盾。

把欧几里得的这个办法做一些小修改，就是令前面的$p$为$p_1p_2\cdots p_m-1$，在做一些程度不大的改变，也可以证明素数是无限的。利用这个改变后的思想可以证明下面一个简单的命题——“有无穷多个型如$4n-1$的素数”。 证明过程是这样的，如果只有有限个$p_1,p_2,\cdots,p_m$互素，令$N=4p_1p_2\cdots p_m-1$。下面的讨论和前面差不多，首先$p_1,p_2,\cdots,p_m$都不是$N$的素因数，所以$N$的素因数只能是型如“$4n+1$”，这样两边除以$4$的余数不一样，矛盾。

第二种办法，用到排列组合的知识，高中生能看懂，叫做数数法。考虑一个正整数$x$,那么不大于$x$的正整数取值方式有$x$种。把每个$2$与$x$之间的正整数唯一地写成$r^2s$形式，其中$s$的素因数都不超过$1$次的。那么$r\le\sqrt{x}$，就是说$r$取值方式最多$[\sqrt{x}]$种，如果只有$m$个素数，那么$s$的取值方式最多$2^m$。于是$[\sqrt{x}]2^m\ge x$。当$x$足够大时，不等式不可能成立。

热身完毕，进入高级模式。

方法三，抽象代数办法。如果$\mathbb{Z}$只有有限个素理想，那么单扩张$\mathbb{Z}[\sqrt{-5}]$是唯一分解整环。但$6=2\cdot3=(1+\sqrt{-5})(1-\sqrt{-5})$，矛盾。注意$1\pm\sqrt{-5}$在这个环下不可分解，不是很显然的，了解抽象代数的读者可以试试证明它。

方法四，再来一个拓扑学的办法。在整数集合中，每个从$-\infty$走到$+\infty$的等差数列中所有的数做成一个集合。用这些集合做基，可以生成一个拓扑。令$A_p=p\mathbb{Z}$那么$A_p$不仅是开集，它还是闭集，这是因为$\mathbb{Z}\setminus A_p=\bigcup\limits_{i=1}^{p-1}\{pn+i~:~n\in\mathbb{Z}\}$是一簇开集的并，即开集，于是补集是闭集。如果只有有限个素数得到$P=\bigcup\limits_{p}A_p$，并集跑遍素数时，得到$P$是闭集。但$\mathbb{Z}\setminus P=\{-1,1\}$不是开集，矛盾。

方法五，集合论来了。在整数集合中，还是用每个从$-\infty$走到$+\infty$的等差数列中所有的数做成一个集合。用这些集合做成集簇$\mathcal{A}$。$\mathcal{A}'=\mathcal{A}\cup\{\emptyset\}$显然对有限交运算封闭，而且用方法四中的办法可以证明，对$A\in\mathcal{A}$有$A^c$可以写成有限个$\mathcal{A}$中成员的并。而且对于有限个$A_1,A_2,\cdots,A_m\in \mathcal{A}$，他们的并的补集不可能是非空有限集。这是因为$F=\left(\bigcup\limits_{i=1}^m A_i\right)^c=\bigcap\limits_{i=1}^m A_i^c$，而每个$A_i$是有限个$\mathcal{A}$中元素的并。再利用一下交并的分配率对有限交的封闭性，得到结果是$F$是有限个$\mathcal{A}'$的并，所以要么是无限集合，要么$\emptyset$。这样，如果素数是有限集，令$F=\{-1,1\}$而$A_p=p\mathbb{Z}$，其中$p$跑遍素数得到矛盾。

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

​

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

原文发表于科学网博客：http://blog.sciencenet.cn/blog-395200-866788.html

 

“倍儿努力”先生何许人？瑞士物理学家、数学家丹尼尔·伯努利(Daniel Bernoulli 1700～1782)是也。通用的译名念起来怎么听都有点像“不努力”，索性称呼为“倍儿努力”也许更贴切，注意要用京味儿的儿化音来读——可参考某晚会歌曲《这个FEEL倍儿爽》的发音。

2月8日是这位 “倍儿努力”先生寿辰，让我们来聊聊这位大名鼎鼎的伯努利家族中最著名的一位吧。与德国的音乐世家巴赫家族的枝繁叶茂相似又不同的是：瑞士的伯努利家族是不折不扣的科学豪门，特别是数学，代代相传，在世界范围内也罕见。三代人中产生了8位数学家、科学家，堪称大家的至少也有三位，而家族后代中在数理科学、工程技术、艺术方面也多有所建树。

丹尼尔1700年生于荷兰格罗宁根。是数学家雅各布的侄子，数学家约翰的次子，这就是最著名的三位“倍儿努力”先生。有趣的是三位走向数学的路也如出一辙，都是违抗父命改行。丹尼尔的爷爷尼古拉斯曾让其伯父雅各布念神学，但他取得学位后还是自学了数学成为数学家。其父约翰原本被安排照料家中事务，在大哥的支持下学医，后受兄影响凭着对数学的热爱，自学成才，这一家在数学方面真称得上是倍儿倍儿的努力。

丹尼尔同样违背了其父要他经商的意愿，先是曲线学医，他21岁取得医学硕士学位，后来还是受父兄的影响而转向了心爱的数学方向。25岁时赴俄国圣彼得堡科学院担任数学教授。在圣彼得堡科学院8年应该是他的黄金时期，完成了关于流体研究的初稿，并与父亲的学生欧拉成为好友，探讨各种数学问题。这期间丹尼尔讲授医学、力学、物理学，做出了富有创造性才能的工作。后来由于健康原因回到瑞士的巴塞尔，并开始了与欧拉之间长达40年为人称颂的科学通信。在通信中，丹尼尔向欧拉提供关心的重要科学信息，欧拉则运用数学才能给以最迅速的帮助。1738年出版他一生中最重要的著作《流体力学》（Hydrodynamica），共13章，提出了超越时代的流体定律。1750年成为物理学教授。一生曾十次荣获法国科学院的年度奖，据说历史上另一位获得同样多次殊荣的恰恰是欧拉。当然其父约翰不愿和他一同获奖而至终身龃龉不合更被视为奇闻，这儿暂不多谈了。

丹尼尔·伯努利的流体定律也被称作伯努利原理，在1726年首先提出。原理其实不难理解：在水流或气流里，如果速度小，压强就大，如果速度大，压强就小。其在重力场中同一高度流动时常被写作简化伯努利方程：

   式中p为流体中某点的压强，v为流体该点的流速，ρ为流体密度。实质是流体的机械能守恒定律体现，适用于忽略粘度、不可被压缩的理想流体。这个看似简单的公式用处可不小，涉及生活的方方面面，对现代航空飞行更是至关重要。

   比如飞机为什么能够受到向上的升力而起飞？这是因为飞行时机翼周围空气流线分布在机翼横截面的上下方不对称所致，上方的流线密流速大、下方的流线疏而流速小。由方程可知机翼上方的压强小,下方的压强大。于是就产生了升力。

   球类运动中的弧线球也可以用它直观的分析出结论，比如贝克汉姆外脚背的弧线弯曲方向与使用内脚背有何不同？乒乓球中的上旋球与下旋球的轨迹如何判断？运用方程都会有很便捷的答案。

   生活中还有许多现象可以从伯努利原理来解释，有兴趣的读者可以深入研究。

丹尼尔·伯努利在世的时候已经享誉欧洲。1747年他成为柏林科学院成员，1748年成为巴黎科学院成员，1750年被选为英国皇家学会会员，他还是波伦亚、伯尔尼、都灵、苏黎世等科学院或科学协会的会员。据说有一次旅行时还很年轻的他向别人自我介绍说，他就是数学家丹尼尔·伯努利，而听者不信，嘲讽地回应道：“那我还是艾萨克·牛顿呢！”由此，其知名度可见一斑。

他的研究领域极为广泛，绝对算得上“倍儿努力”。著作数量庞大，据统计其全部数学、力学著作和论文超过80种，工作几乎涉及当时的数学和物理学的研究前沿的所有问题：如流体问题、振动和摆动问题、引力、潮汐、磁学、船体的稳定等，并率先将微分方程应用到物理领域，被推崇为数学物理方法的奠基人。在纯数学方面，涉及到代数、微积分、级数理论、微分方程、概率论等重要方面。不愧是天才骄纵啊…

且慢！

巧合的是，同在2月8日出生、并在圣彼得堡发现化学元素周期性的化学家门捷列夫（1834-1907）就否认所谓的天才，他曾平静地说：“什么是天才？终身勤奋就是天才！”

所以，致敬“倍儿努力”！

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

对于做学术的人们，是非常看重自己发表的论文的引用量的。因为，一般认为，论文被引用数据来反映论文作者的水平，反映论文的价值。论文被引用次数越多，说明论文价值越大，作者的水平越高。很多时候，一篇学界大家发表于顶级杂志的论文在短期内被很多人引用，但有时时候也不尽然，有的论文被引用的次数很少，有的甚至“零引用”。

 

还有一种现象，一篇论文在发表初期，甚至在发表后几年、几十年都引用者寥寥，但之后被引用数量“大爆发”，成为被引用大户。这样的论文，就叫做“睡美人”论文，这些论文就像沉睡的公主一样，一旦被唤醒，就不断散发着她诱人的气息。对于这个现象，还有一种更专业的说法叫做“延迟承认”(Delayed Recognition)。俗话说，书中自有“颜如玉”，论文中也有“睡美人”。

 

2014年10月30日出版的《自然》杂志讨论了史上被引次数最高的100篇文献。列在第11位的是美国统计学家Edward Kaplan和Paul Meier发表于1958年第53卷《美国统计学会会刊》上的论文，这是一篇典型的“睡美人”文献。他发表后几乎没有什么人去引用，直到十几二十年后的20世纪70年代，由于计算机能力的增强，使得该文介绍的方法——Kaplan-Meier方法——连非专家都能掌握了。该方法简洁、易于使用，故引用者众。据了解，此文已被引用超过4万次了。

 

武夷山教授是中国科学技术发展战略研究院研究员，他对论文文献中的“睡美人”现象也颇也研究。他说：“千万不能忽视文献‘睡美人’现象。……如果我们在文献收藏上短视的话，等“睡美人”文献苏醒之时，恐怕已经找不到这些文献了。”

 

 

附录：Kaplan-Meier方法介绍（来源于网络）

 

Kaplan-Meier生存曲线

随访研究，如对 某人群进行跟踪，直至出现一个特殊事件或终点，如死亡、癌症复发等，对所有研究对象从某特定时间点开始追踪，记录出现特殊事件的时间。通常，当所有研究对 象出现该事件时研究才结束，但也有些研究对象可能失访，或者研究提前结束，这样就有一些对象的结局未知，对这些对象记录跟踪的时间（截尾数据）。 
Kaplan-Meier生存曲线可以用来描述该人群的生存情况。 

Kaplan-Meier方 法是一种非参数方法，既适用于小样本，又适用于大样本。基本思想是：将生存时间由小到大依次排列，在每个死亡点上，计算其期 初人数、死亡人数、死亡概率、生存概率和生存率。其思想与寿命表法相同。只不过寿命表法中时间段的划分是人为的、等距的，而Kaplan-Meier法划分时间段的分割点是实际死亡发生时间。

Kaplan-Meier方法的可用来 
1． 估计某研究因素 不同水平的中位生存时间。 
2． 比较该研究因素 不同水平的生存曲线有无差异。 
3． 控制一分层因素 后对研究因素不同水平的生存时间比较（此时将按分层因素的不同水平对研究因素对生存时间的影响分别进行分析）。

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

编者注：本文作者系我国已故著名数学家苏步青。此文从苏步青网转发。在西方情人节即将到来之际，哆嗒数学网与大家一起分享老一辈数学大师跨越战争年代的跨国恋情。我们一直认为，每一位热爱数学的人一定也热爱自己的生活，也会拥有真挚的爱情。在这里，祝大家都幸福。

 

   年轻时，我在日本仙台的东北帝国大学留学。不久，认识了松本教授的爱女松本米子。

　　

　　在樱花盛开的季节，我们由恋爱而结婚。那年她二十三岁。

　　

 

　　对于我们的婚姻，她的父亲不太赞成，但是她的母亲很支持。在我们结婚时，因为害怕亲戚们嘲笑我是个中国人，不敢暴露我的真实的国籍。直到我获得了理学博士学位，日本报纸都报道了一个中国留学生的成就，他们才知道了我的真正国籍，他们暗说：“这么厉害的中国人，为什么不早告诉我们？”

　　

　　我获得学位以后，便决定回国。那时，很多人都劝我别回中国，他们为我保留了讲师的工资和博士研究生的助学金，这足够我们一家子开销了。但是她对我说，她很喜欢我，她支持我回中国，为我们的两个孩子的教育着想，我们也应该回中国去。不久，我们一家到了西子湖畔的杭州城。从那时起，她就生活在中国的大地上，一直到离开人间。

　　

　　刚到中国，她在生活上很不习惯，就说吃吧，起初她很讨厌乳腐，说太脏了。我说那么好的东西不吃太可惜了，就趁她不注意，把乳腐进行了“改造”：把乳腐上的一层皮去掉，还加了白糖。后来，她就很爱吃了。皮蛋，日本也没有，慢慢地，她也习惯那种特殊的香味儿了。那时，在杭州的日本领事馆通过各种关系来对她说，你是日本人，在中国吃东西不方便，早上就到我们这里来吃吧。可是在杭州几年，她一次也没有去过。再说洗澡吧，日本人的习惯是每天都要洗的，到了中国以后，没有那样便利的条件了。为了解决这个矛盾，我请人用铁桶做了一个浴缸，但也只能满足她一星期洗一次，后来她对此也习以为常了。

　　

　　抗战开始后，平静的生活被日本侵略者的炮声打破了。从此，我们开始了一段艰难的生活。我随学校内迁到了贵州，我的夫人独自带着孩子回老家，逃难中的人们，又哪有心思去欣赏那大自然的风光呢？相反，她又面临了一个新的困难：不懂浙江话。

　　

　　故乡的人们以极大的热情欢迎这位远道而来的媳妇，他们帮助她料理一切家务事，洗菜、淘米、做饭，常常有人悄悄地帮她干好了。

　　

　　她生活在温暖之中，与乡亲们建立了浓厚的情谊。她常常用她微薄的力量为乡亲们做一点事儿。一直到新中国成立后，她和乡亲们仍然保持着那种真挚的感情。不管是关系多远的亲戚上我家来，她都要亲自迎接，为他们安排食宿，从不表示厌烦。直到现在，我家乡的人有时还会说：要不是苏老太太，我们还真进不了苏家的门，苏先生太忙了。

　　

　　每当听到这些，我就感到脸红。因为我自己对频频来访的乡亲们，有时会感到厌烦。

　　

　　战时生活非常艰苦，我整天忙于教学和科研，很少能顾及家庭。

　　

　　家里再也请不起保姆了，几个孩子和许许多多的家务，全靠她一个人照顾。一个日本的富家女子，在中国人民的抗日战争的岁月中，默默地为一个中国家庭费尽了心血。

　　

　　我记得，在我们的婚礼上，她穿的是非常漂亮的礼服。可是自从抗战以后，她就再也没有心思，也没有机会去做一套好一点的衣服了。

　　

　　她心里想的是我和孩子们的温暖。

　　

　　她在少年时代，是高级女子学校的高材生，她有比较高的文化素养和艺术造诣。弹奏古筝是她的一大爱好，听说还常上广播电台去播音。结婚以后，她带了一把十三弦的古筝随我一起来到了中国。至今，这把琴依然在我的房间里。每当我抚摸琴身，弹拨出一阵阵琴声，我便仿佛又看见她坐在琴前，轻弹慢拨，沉浸在悠扬的古曲声中的形象。

　　

　　可是，在那个年代里，琴身蒙上了一层又一层的灰尘，她再也没有工夫去抚弄它了。

 

　　

　　那时，她还放弃了自己心爱的书法艺术。她的书法很有功底，有一次我的一个学生对我说：“苏师母的字要比苏先生的好得多。”正是在她的影响下，我才认真地临帖习字，有点进步。在我们的晚年，我常常拿着替朋友们写的条幅到楼上去请她过目，尽管她躺在床上，目光还是那么锐利，常常指出这样那样的缺点。

　　

　　她牺牲了自己的一切，帮助我在艰难的岁月里，取得了教学、科研上的一点成绩，她还担当起教育八个孩子的任务。我一直认为，没有我的夫人，我不可能培养出那么多的学生，取得数学研究上的成果。

 

 

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

编者注：本文是作者刚刚度过数学专业的大一“菜鸟季”，写下的一篇数学分析学习心得，与各位网友分享。应作者要求，通过哆嗒数学网匿名发布。同时哆嗒数学网欢迎大家投稿，QQ：1178853280 。

 

数学分析，简称数分，主要内容是微积分，是数学专业数学学习的开端，也是通往未来更高等数学的开端。同样，它是分析方向的基础，学好数学分析非常重要。

 

数分和中学数学有着非常大的区别，可以说，中学和中学以前的数学，都是在介绍各种运算法则，理论性的东西非常之少。到了数分上，就有了非常多的理解性东西，虽然某些概念的定义仍然是用数学符号表达，但是要想完全彻底的理解概念，还是要做深入的思考，而不是像中学那样，仅仅是训练公式的熟练度。

 

对任何一门学科，教材和题集的选取都是至关重要的。这里说下笔者的体会，华东师大的两本书很适合入门，也是普遍普通数学系的数分教材。但是数分是很多后面科目的基础，包括后续的分析内容，实复分析，泛函调和分析，还有一些其他分支，例如微分几何，微分方程等等，一本好的数分教材应该稍微涉及到其他数学科目的基本概念。

 

这里推荐徐森林的《数学分析》。笔者在自学这套教材之后，发现它和普通数分教材比，有很多优点，列举如下:在讲授单元积分学时，本书通过引入零测集的概念，给出可积的充要条件，这对后续学习测度论有益；在讲授多元极限前，普遍本科生已经熟悉了单元极限，本书在此引入了拓扑学的一些基本概念，拓扑，度量空间，紧致集等，首先把开集推广到一般情况，进而把极限以及连续性推广到一般拓扑空间上，最后将连续性的一些定理推广到了一般拓扑空间上，这样，单元中所接触到的单侧极限，广义极限也仅仅是特例，再讲授多元极限，自然水到渠成；在讲授傅里叶级数时，引入了傅里叶积分和傅里叶变换，它们是调和分析的内容，可以用来计算某些含三角函数的积分的简便公式；在讲授多元积分的三大公式——斯托克斯公式、高斯公式、格林公式时，本书借助微分形式和外微分算子，将他们统一成一个公式，公式的统一既深入理解了三大公式的关系，又对后续学习流形有益。

 

俄罗斯有一套《微积分学教程》，国内的很多数分教材都深受本书影响，本书可以说是数分的一本工具书，它含有大量的例题，并且内容非常丰富，包含了很多普遍教材没有的内容，例如绪论的通过证明有理数的不完备性，引入无理数，再证明实数完备性的内容，是大部分数分教材没有篇幅可以介绍的；高阶导数部分介绍埃尔米特差值公式；不定积分处介绍椭圆积分；正项级数的库默尔判别法;函数项级数处的拟一致收敛等等。但是本书是20世纪初所著的，当时测度论还不完善，所以并不包含比如可积的充要条件为不连续的点是零测集，这样的重要内容。对有能力的学生，可以选择卢丁(Rudin)的《数学分析原理》， 本书是作者卢丁所著的分析三部曲第一本，后两本则是《实分析和复分析》与《泛函分析》。这本书比上述教材都更有难度，因为它是直接从拓扑角度讲数分的，并且为了和后两本衔接，还引入了基本测度论。对于有能力的同学不妨一试。

 

 

下面说题集。对于大多数学生，天资并没达到天才的层次，光看教材是不能完全理解理论的，这一点越到后面更难的科目更能体现出来。应用理论解决问题，是理解理论的重要途径。但是，如果仅仅是看解答，并不会有太大进步的，经常直接看解答会让你对答案产生依赖，懒惰会让你不再独立思考，这就相当于你是在拄着拐杖走路。一旦到了需要独立解决问题的时候，就相当于拿走了你的拐杖，这时便很难行走了。因此，做题时独立思考是非常重要的，可以毫不夸张的说，独立做出一道题，比看十个解答都有用。这里按难度从易到难，推荐如下题集: 裴礼文的《数学分析中的典型问题与方法》，这本书很适合准备考研；徐森林的《数学分析精选习题全解》这套就是和徐森林的《数学分析》配套的题集，值得一提的是科大的数分教材史济怀和常庚哲合著的《数学分析教程》上大部分有难度的课后习题，都可以在本书中找到解答；周民强《数学分析习题演练》，这一套很有难度，事实上大多题目来自W.J.Kaczor和M.T.Nowak所著的三本题集《Problems in Mathematical Analysis》；Poyla的《数学分析中的问题和定理》，Polya大师的这一套虽然是题集，但是观点非常高，可以说是数分难题的顶峰，借助问题来引出各种定理和技巧。最后推荐的这本书，笔者认为是学习数学分析的必读书目，但是笔者发现很难将它分在教材还是题集中，因此放在最后介绍，这套书叫谢慧民等著的《数学分析习题课讲义》，分上下两册，可以算作带有题集的学习辅导书。大部分学习辅导书，都是通过重述定理定义内容以及题目和解答来"讲"概念和定理的，本书却大篇幅的具体讲述各种定理该如何理解，一些相似概念的区别和联系，说它是难得的一套从浅如深理解数分的好书绝不为过。每一章最后，都有参考题，难度适中，缺点是题目没有给出解答或提示，这对初学者来说十分不方便。

 

 

自己看书做题是一方面，和他人讨论是更好的学习方式。可以参加学校组织的或者个人组织的研讨班，包括讨论定理或概念该如何理解，自己遇到困难的题目有哪些思路。还可以在一些数学网站上讨论数学，在较正规的数学网站上发言，往往需要LaTeX 打公式，有兴趣的学生可以自学下，并不是很难。

 

最后笔者推荐几个数学网站。这是博士数学论坛(Math.org.cn)，是国内最专业的数学网站，有很多高校的数学高手和数学系老师常驻。SE数学版(math.StackExchange.com)}这是国内外比较火的数学网站，它是MO(MathOverFlow.net)下的网站，后者是研究级别的数学网站，包括陶哲轩在内的很多数学家都在上面讨论。SE是为了保证后者讨论质量而建立的适合本科生讨论问题的网站(实际上SE接受任何水平的数学问题——哆嗒数学网注)，可惜数分模块中的问题更多的是计算，理论性不多。还有是罗马尼亚的"解题的艺术"网站(ArtOfProblemSolving.com)的数分模块。

 

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

数学是不是越来越火了？至少美国人想把它做火！

 

2015年2月3日美国国家数学研究所(MSRI)与美国普林斯顿高等研究院(IAS)联合宣布：首届美国国家数学节将在4月18日星期六于美国首都华盛顿召开。而美国国家数学研究所与普林斯顿高等研究院将成为这次数学节的主办单位。

 

 

史密森学会(SI)将成为这是数学节的协办单位，将组织不下30场的演出、展览以及讲座，并开展终身学习者激励初学者的活动。所有活动向公众开放并且免费。各类活动将在伊妮德答豪普特花园、狄龙·利波雷中心、美国国家自然历史博物馆、美国国家航空航天博物馆、美国非洲艺术馆、弗里尔美术馆和萨克勒美术馆等地分别举行。

 

 

这次数学节，并非某学习机构，或者某商家刻意为之商业节日（双十一之类弱爆了——哆嗒数学网注）。从主办单位和协办单位的背景就可见一斑。

 

美国国家数学研究所(Mathematical Science Research Institute, MSRI)，成立于1982年，著名数学大师陈省身是创立人之一，并担任第一任所长。美国国家数学研究所是当今世界最卓越的数学合作研究机构，每年有数以千计的数学家与该机构展开合作。当然，美国国家数学研究所被人称道的不仅仅是因为他高质量以及领先世界的基础学术研究，数学教育以及数学公众传播方面的工作也常常被人“点赞”。

 

普林斯顿高等研究院(Institute for Advanced Study, IAS)，1930年成立于美国新泽西州普林斯顿。普林斯顿高等研究院与普林斯顿大学虽有渊源，但其并不是普林斯顿大学的一部分。普林斯顿高等研究院是各个领域的最一流学者做最纯粹的尖端研究，而不受任何教学任务、科研资金或者赞助商压力的研究机构。曾经在这里工作的“大人物”的名字都如雷贯耳：爱因斯坦、哥德尔、冯·洛伊曼、小平邦彦、杨振宁、李政道……，到了今天，在数学方面，此机构还有不少于5名的菲尔兹及沃尔夫奖得主的固定研究人员。

 

史密森学会(Smithsonian Institution, SI)) 1846年根据美国国会法令创立，直接隶属于国会，是唯一由美国政府资助、半官方性质的第三部门博物馆机构，同时也拥有世界最大的博物馆系统和研究联合体。史密森学会的管理和经费来源于由美国政府拨款。该组织囊括19 座博物馆、9座研究中心、美术馆和国家动物园以及1365亿件艺术品和标本。董事会由美国最高法院首席大法官、副总统、3名参议员、3名众议员和6名非官方人士组成。

 

有了强力机构对盛会的支持，美国国家数学研究所所长Eisenbud信心十足的表示：“数学在我们每一个人身边——从彩虹的色彩到我们开的汽车以及开车经过的大桥，从现代智能手机和互联网贸易到最新的医疗技术，从“下五洋捉鳖”的深海研究到“上九天揽月”天文研究——这次盛会将成为数学展示它趣味与美的舞台：数学，每个人能懂，每个人能乐享其中。”

 

数学节的官网宣传语说，将给我们从未有过的数学体验，那么我们一起期待吧！

 

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

数学已经成为人类步入现代化的核心工具与中心思想。大到卫星上天，小到一个app应用，都离不开数学——只是你是否知道而已。

 

但是，请和我们哆嗒数学网的小编一起想象一下。远在数学还没有给我们带来计算机、量子力学和卫星定位系统之前的古代，一些最聪明的大脑已经在不断的发现他们的数学成就。这些发现建立了最基本的数学思想和工具，带领我们走进了现代化的生活。这是多么神奇的事情。

 

下面列出的12位数学家，就是这些人中的佼佼者。他们的发现，形成了世界走入现代化的数学基石，也是我们步入现代生活最重要的一系列成就。

 

 

 

毕达哥拉斯 (约前500年)

 

 

毕达哥拉斯其实不只一位，他有很多追随者，他们形成了一个学派。他们对数的崇拜有着宗教的神秘主义色彩。带着对神的崇敬来研究几何与数字。

 

毕达哥拉斯学派最有名的数学成果当属毕达哥拉斯定理：对于一个直角三角形，两直角边的平方和等于斜边的平方。这是平面几何最基本的结果之一。

 

毕达哥拉斯学派的故事说明了数学和这样宗教如果结合是多么的危险。毕达哥拉斯学派神化的整数，认为整数是宇宙的基石。他们研究几何与音乐，只要和数量相关的东西都认为是两个整数的商。

 

毕达哥拉斯的一个追随者道如何把一个直角边长等于1的等腰直角三角形的斜边用两个整数的商表示出来。但是他的结果是：这是不可能的。用现代人的说法就是，2的平方根是一个无理数。

 

故事的结局是悲惨的。当这位追随者把它的关于可能存在无理数——一种不能表示成两整数之商的数——的事实告诉同伴时。同伴们很震惊，但也很愤怒，把这位有重大发现的追随者装上了船，扔进水里淹死了。

欧几里得(约前300年)

 

 

欧几里得是古西腊最伟大的数学家之一。

 

在他的传世之作《几何原本》中，欧几里得建议了一个几何学的框架。正当诸如毕达哥拉斯们的其他古西腊先哲们还在纠结于关于数的问题的时候，欧几里得已经开始引进他严谨的论证体系了：从为数学多的关于点、线的公理出发，通过不断演绎推理，建立了一套在当时最系统化的几何学。

 

这种从公理开始，不断推导结果，而每个新结果都由之前推导出的结果为依据的严谨论证思想，可能是2000多年的历史长河中，最据支配地位的思想。

 

         

阿基米德 (约前287-前212)

 

 

阿基米德可能是所有时代最伟大的数学家。他最被人熟知的贡献是他早期物理学的发现。他发现了杠杆原理，和浮力定律。一个大家都知道的传说：有一天，阿基米德在洗澡，看见洗澡水从澡盆里的漫了出来，于是他兴奋，裸奔上了大街，嘴里兴奋地尖叫：“我发现了！”

 

作为数学家的阿基米德甚至比他在物理中做得更好。他已经能够把圆周率估算到一个非常好的精确值，以及计算抛物线围成的一些图形的面积。

 

这些成就让人惊奇的真正原因是，阿基米德使用的计算方法和1800年后牛顿和莱布尼兹发明的微积分中的计算方法惊人的相似。他用不断的添加更细致多边形的来接近图形，这样多边形的面积就会和想要计算的面积的差距越来越小。这样的方法，让人强烈的联想到现代的极限思想。阿基米德这样的数学智慧，领先了他所处时代将近两千年。

 

 

花拉子米(约780-850)

 

 

花拉子米是9世纪的数学家，他创造了很多基础的计算技术与方法。他最大的贡献是他发明了一套做算术和解方程的形式化、系统化的办法。花拉子米在他的著作中，使用了印度人的发明的阿拉伯数字体系并流传到了欧洲。而阿拉伯数字体系比之前用的罗马数字体系或者其他非按位数字体系，在加减乘除的表示方面更为简洁。

 

花拉子米还建立了一套解基本方程的规则体系，比如4x + 8 = 2, x²- 8 = 4，在今天这套体系叫做代数。实际上，“代数”这个词就来源于他书中解方程那部分内容的标题，还有一个词是“算法”，它表示解决数学问题的系统流程，这其实是花拉子米的拉丁文名字。

 

 

纳皮尔(1550-1617)

 

 

这个榜单的其他数学家在各个数学分支都有大量的贡献，而纳皮尔只有一个发明，但这个发明极为重要：对数。简单的说，一个数的对数让我们知道了这个数额数量级。

 

用现在的话来说，对数有一个“底数”，一个数的对数就是得到一个数，使得这个底数的那么多次方等于这个数。比如，以10为底数，10的对数是1,100的对数是2。因为10的1次方等于10，10的平方，就是2次方等于100。

 

对数之所以这么有用，是一个重要原因是由于它的一些性质：对数能把乘法变成加法，把除法变成减法。更确切的讲，两个数乘积的对数等于这两个数分别取对数在加起来。同样，两数商的对数等于两数对数的差。

 

在没有计算机的年代，这个性质打打降低计算的难度。对两个非常大或者非常精细的小数做乘除法要比做加减法的时间长得多。所以，如果有人要对两个大数做乘法，他可以先查对数表的得到两个数的对数，在加起来，然后再用对数表返查得到结果。

 

一些计算工具，比如说计算尺，利用对数来做快速计算。这种快速计算器在科学和航海中派上了打用场，我们可以非常快得做一些大数的计算。

 

很多用数量级来衡量计量单位也是用对数来衡量的。比如地震中的里氏震级，以及衡量声音大小的分贝。

 

 

开普勒(1571-1630)

 

 

开普勒是一位天才的几何学家，他把他的数学能力强化了人们对太阳系的认识。开普勒曾经是伟大的天文观测家的第谷·布拉赫助手，而布拉赫拥有一些在当时最细致的行星运动的记录资料。通过分析这些资料，开普勒能够确定和改进哥白尼的太阳系观点：行星围着太阳转，而转动的时间是基于椭圆形状的行星轨道用并用精确定义的数学定律来描述的。

 

开普勒定律是一个伟大发现，因为它是对物理过程精确且简洁描述。像行星绕太阳的轨道这样，我们世界的事物遵循这各种各样的规律。20世纪的物理学家维格纳有一个优美的表述，“数学无理由的有效性”。开普勒定律就是这种无理由的有效性的早期例子。

 

开普勒定律也为牛顿发现他的牛顿运动律提供了条件，尤其是万有引力定律。开普勒对天体力学的贡献让美国国家航空航天局(NASA)将研究太阳系以外的行星的项目以他的名字命名，叫做开普勒任务。

 

 

笛卡尔(1596-1650)

 

 

笛卡尔最被人熟知的是他对哲学的贡献。他提出了精神与物质二元论(心物二元论)，他还有一句名言：“我思故我在。”。但是，我们今天使用的大部分数学都欠笛卡尔一份“小恩情”。

 

笛卡尔对数学最重要的一份贡献就是创立了解析几何。数学在笛卡尔之前的历史长河中，代数和几何是互不联系的两个学科。一方面，我们有我们对数字和未知量进行符号化和抽象的操作。另一方面，我们又对一些平面图形和立体图形进行研究。

 

笛卡尔的解析几何统一了这两个领域。他开拓了一种把代数式和方程用坐标平面上的直线或者曲线表示的思想。他的这种基本思想至在今天的中学课程中还在学习。学生们还在练习把y=3x+5这样的方程画成直线，或者把y = x² – 4这样的方程画成抛物线。

 

这种几何与代数的结合是之后创立微积分的重要前置条件，同样，它还理所当然的还是现代数学的核心思想。为了纪念的卡尔如此重要的奠基性工作，我们把他发明坐标系定名为“笛卡尔坐标平面”。

 

 

 

 

帕斯卡(1623-1662)

 

 

法国数学家帕斯卡和这榜单的其他很多数学家一样，在数学的很多领域都有贡献。帕斯卡三角形(中国叫做杨辉三角)提供了一套计算二项式系数的漂亮方法，而二项式系数在代数和其他分支非常重要。他还发明了世界上第一台机械计算器，是现代计算机的早期原始版本。

 

帕斯卡同样还是概率论的创立者之一，他在分析游戏的取胜机会时候开创了这个理论。帕斯卡关于基本概率的工作，让我们开始有能力用数学方法理解机会与风险。

 

帕斯卡把他的概率理论用于神学研究，他提出“帕斯卡赌局”的理论，用于说明为什么我们应该相信神的存在。

 

 

 

牛顿 (1642-1727)

 

 

任何一个关于伟大数学家的榜单都不会没有牛顿。他发明了微积分(这个成就与下一位数学家分享)，数学第一次可以系统的描述物体在时空中的变化。牛顿是在发展他的物理理论的时候发明微积分的。

 

微积分是描述运动最自然的语言。汽车的速度是位移的变化率，或者说是位移的导数。把一个铁球从高楼上释放下落，他的速度是变化的，速度的变化率或者说速度的导数就是加速度。牛顿还知道加速度是地心引力作用于铁球质量上的结果。

 

牛顿的物理学还是整个人类世界物理观的里程碑。早期的物理学家和天文学家，比如前面提到的开普勒，他们已经知道天体的运动和一些变量有关。但牛顿和其他的一些物理学家借助数学工具，能让人知道为什么天体运动和这些参数有关。

 

更进一步，牛顿定律是一个普适性理论，它让人明白，让铁球加速下落的力和让月亮绕地球转的力都是相同的力——地心引力。同样的物理定律被应用于宇宙的任何地方，成为科学的核心理论，也被已知的证据支持。

 

 

莱布尼兹 (1646-1716)

 

 

在牛顿于英格兰发明微积分的同时，莱布尼兹在德国独立的发明了微积分，然后在数学家之间引发了一场关于微积分发明权的争论。但无论如何，莱布尼兹当时使用的很多微积分的符号一直沿用至今。

 

莱布尼兹同时在各个方面预见了数学之后的发展。他笃信理性主义，他专注的形式符号逻辑在19世纪末20世纪初发展成了现代数理逻辑和集合论。莱布尼兹和帕斯卡一样还参与了机械计算器的改进的研究。

 

贝叶斯 (约1701-1761)

 

 

贝叶斯提供了关于概率论与数理统计最重要的工具之一。这个工具让我们对概率的研究能够进行更加艰巨的探索。

 

如果我们知道一个事件发生的内在机制，那么我们计算着事件的概率是非常简单的。用基本的计算，我们能算出打扑克梭哈时，得到同花顺的概率，或者扔硬币时，连续5次都是正面的概率，再或者彩票中奖的概率。

 

但更多时候，我们更关心把上述问题反过来的情况。我们不去计算基于知道发生机制的事件的概率，而是基于观察到的现象，想得到和了解不知道发生机制的事件的发生的可能性。

 

我们需要了解在一些情况下基于观测现象背后的关联性。比如医学（如果检测为阳性，患病的可能有多大？）、比如社会科学（基于历史数据，最好的解释通货膨胀与失业率之间关系的模型是什么？）、比如日常生活（如果女孩同意和我去另外一家酒吧，他对我有意思的可能性有多大？）。

 

贝叶斯定理提供了一个形式化的工具，让我们能回答这些问题。当一种事情已经发生的条件下，定理让我们能计算这样的概率，当特定事件发生时，鉴于观测结果，基于我们把观测结果纳入特定事件看是否发生，这样能同时得到先前事件在特定事件下发生的可能性。

 

贝叶斯定理是一个分析信息缘由的强大工具，它还是整个统计学思想的底层框架。

 

 

欧拉 (1707-1783)

 

 

在牛顿和莱布尼兹之后，欧拉接过了对微积分的研究的工作。他引入了现代函数的概念：一条规则，或者说几条规则，用于把一个数变化成另外一个数。在当今数学中，这个概念把所以不相关的分支联系到了一起：线性方程、多项式方程、三角几何，甚至我们测量平面上两点间的距离的办法都能理解和表示为一系列函数以及操作它们的办法。

 

欧拉同样发展了幂级数理论：一个把复杂函数用无限个简单项之和来表示的方法。他研究了三角函数和指数函数的幂级数，让他发现了一个特别的，但很常用很重要的一个公式，著名的欧拉公式$e^{iπ}+1=0$。

 

欧拉还是最多产的数学家之一，在很多领域都有贡献。他对哥尼斯堡七桥问题的解决被认为是最早的拓扑和图论成果之一。