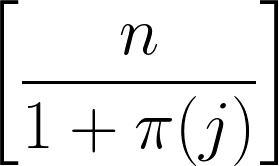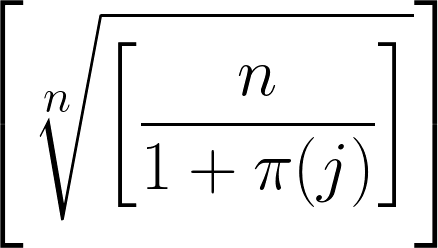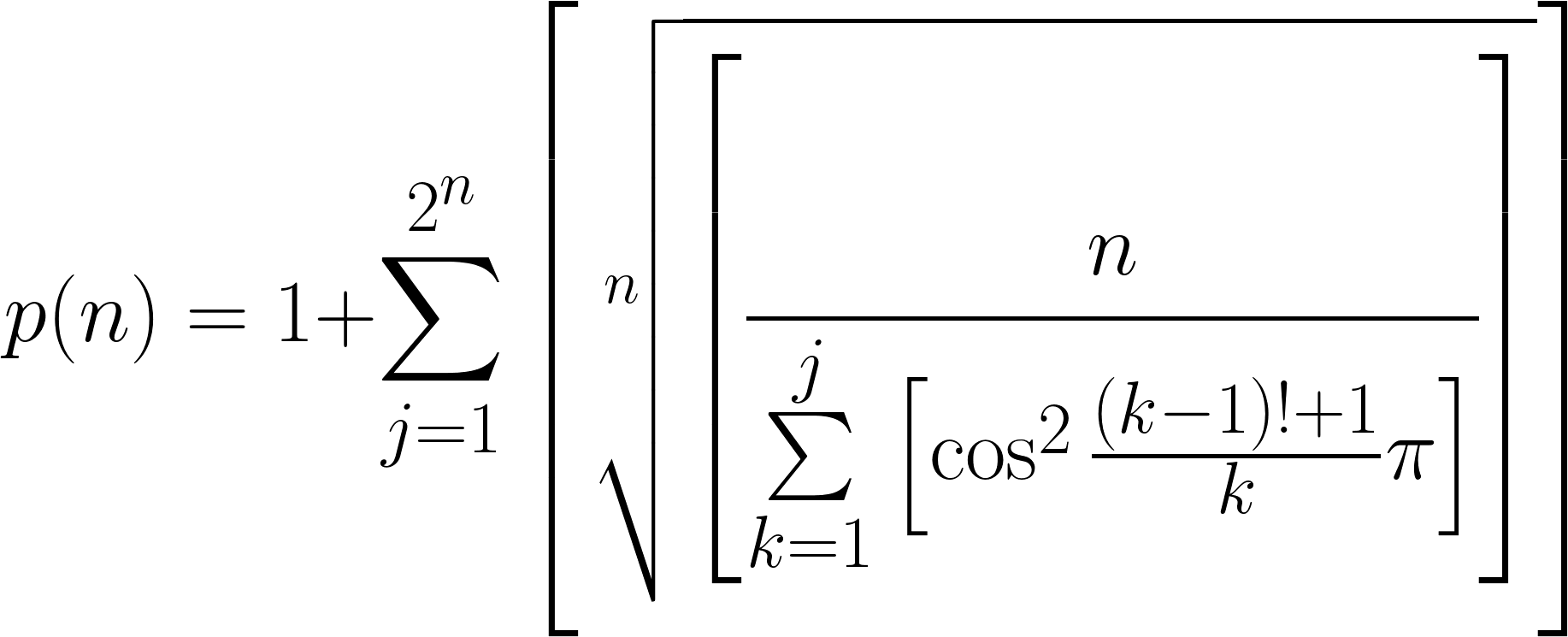我的爱豆是数学家小平邦彦
作者,候尚庶博士, 哆嗒数学网群友 。
关注 哆嗒数学网 每天获得更多数学趣文
哆嗒小编按:此文作者是小平邦彦的超级大粉丝。长期在各个渠道逢人就推荐小平邦彦的数学著作。终于,他们的事情被出版小平邦彦中文版著作的图灵新知知道,并且授予了他图灵优秀读者的荣誉,算是对他的鼓励吧。
这篇文章有非常明显爱豆情节,请读者理解。另外,文章中提到的阅读细节,对需要买这本书的人可能会有帮助。
2008年年末的时候,我在长沙定王台的湖南图书城瞎转悠,看见两个小同学在数学专柜那里,我路过一看,她们在拿着一本不太厚的书在翻阅,书名是《微积分入门I》,作者是一个从未听说过的数学家,叫小平邦彦。等她们走后,我拿起书翻了翻,封底上写着这位数学家卓越的事迹,于是我怀着不屑一顾的心情,最终还是自己买了一本,因为我当时根本不相信,一本号称入门的微积分教材,这个老头写出来的能换出啥子花样。

很快,我为我自己的无知尝到了苦头。第一章的第一节,类似于讲故事,当时我根本没有品读出多少有用的知识出来,然后到了第8面的定理1.1,证明两个实数,α与β,这两个实数的大小关系,大于,小于,等于有且只有一种是成立的,我一看,这不废话吗?这有啥子好说的?而且,他的那种证法,和要证的命题,看似毫无瓜葛。这老头在搞啥?但是好在当时我闲来无事,又有一股子倔驴脾气,我和这个题目杠上了,拿在手里慢慢想,慢慢琢磨。最终,我通过对他的那个证法展开的结果,发现他在书中想告诉我的是,如果大于小于等于三个都不成立,这是不可能的。那么,这和要证明只有一个成立,又有什么关系呢?无奈中,我有一次无意中掰着手指头玩,突然间脑袋灵光一闪,找到了解决问题的钥匙:大于小于等于,类似于食指,中指,无名指,成立我们可以视为伸直,不成立我们视为弯曲,那么我们假设伸直与弯曲之间没有中间状态,三个手指头,就可以演示出四种情况:三个手指头都弯曲,伸直一个,伸直两个,伸直三个。这四种状态有且只有一种是成立的,没有两种同时成立的情况,也不可能都不成立,更无另外第五种情况,书中论证了三个手指头都弯曲的情况,那么以此为指针,根据前一面的实数的定义,和上文中,实数大小的定义,剩下的两种同事成立,三种同时成立的情况,很容易证伪,最终留下一种可行的情况,那就是有且只有一种情况是成立的。
当我想明白这一步的时候,突如醍醐灌顶,原来这本书的布局如此精妙。后来慢慢的往前读,我才发现,这个书很多地方写得很简略,但是该给的指针都给出了。作者督促读者在学习中要反复阅读课文,反复思考道理,而此书布局最令人惊叹的地方,就是一个简单直接的道理:你不把前面的书看明白,不把道理想明白,我让你后面的根本根本看不懂!所以,小平邦彦大师写的不仅仅是一本数学书,他同时把数学的教学法,学生该掌握的学习法都包容在这本书里,真正以知识和正确的学习方法去浇灌读者,而不是停留在教会做题之上,这对于现在这个浮躁的数学学习范围,以应试为目的的数学学习动力,无异于一股能沉降浑浊的清流,而且最重要的是,不从知识和方法的根本上去学习数学,只看习题和分数,那是无源之水无本之木,不可能走得很远的。小平邦彦大师的书中,文字清晰而精炼,很多东西写一半留一半,初看上去冰冷而晦涩,有点严肃,但是深入进去才知道,里面浸透着作者满满的温情与期盼,在严格的思考训练的过程中,我们可以感受到作者那种特有的,以睿智为途径表达给读者们的慈爱。
曾经,有言论拿辛钦的《数学分析八讲》与小平邦彦的《微积分入门》打比,辛钦的行文中,对数学知识的讲述极尽详实,对初学者很友好,确矣。这就好比,我们要过一条河,辛钦先对地质水文气象做了大量的功课,盐后在河上建立起了一座相当坚固的大桥,再把所有的资料都交给读者。这条河哪里水深多少,哪里流速多少,最近这些年的水文情况如何,哪里有旋涡,甚至哪里有落水鬼,都写得清清楚楚,他根据这些数据,建起了一座大桥,这座桥限速多少,承重多少,哪里风速多少,也都告知得清清楚楚,剩下的只要你走过去了。但是小平邦彦的书,风格则完全不同,他只给出你几样最简单的工具,还有一个资料库,你若是想建桥,可以,里面有图纸;你若是想造船,也可以,里面也有图纸。并且,最重要的是,他会在资料库中留给你一个保命的救生圈,找到这个救生圈,就至少不会溺死。剩下的,就靠你自己去摸索实践了。
在实践中学到的知识,那是很有收获感的,并且,你会发现,他给你的那几样最基本的工具,那简直太好用了。所以,我个人认为,如果有一处风景区,电视台花大价钱拍了一部记录片,详细的记录了里面的风景和特色,播放出来之后,给人们的收获,其实是不如自己拿着一块罗盘,一张地图去实地勘测一遍来得充实的。而小平邦彦交给我们的,就是这块罗盘和这张地图。文字上的精炼,与思想上的深厚与丰富,这样看似矛盾的特性在小平邦彦的书中并行不悖的体现出来,其实并不矛盾。因为精炼的是他的写法,深厚的是他的学识,深远的是他的眼光,充实的是读者的头脑,升华的是读者的灵魂,提升的是读者的数学素养。
也有人用菲赫金哥尔茨的《微积分教程》,还有柯朗的《微积分和数学分析引论》与小平邦彦的书相比,前两部书,有很大的相似性,都是由大家所写,而且都很注重数学在物理中的应用,菲赫金哥尔茨是实分析列宁格勒学派的创始人,而柯朗本身就是一位数学物理大家。小平邦彦的书中,偏向于纯理论,没有一句话讲的是实际应用。作为站在人类智慧与文明的顶峰的那群人中的一个,小平邦彦应该深知,知识学明白了,能产生多大的战斗力,他已经无意教我们如何去运用知识了,他想教会我们的,应该是如何获取知识,知识都能自己获取了,应用这些知识的范围,应该是天高海阔的。从我搜集到的信息来看,1935年小平邦彦到东京大学学习数学,38年开始又在东京大学学习了三年的物理,那他真不懂物理吗?未必!
日本向来有大师级的数学家来写中小学教材的传统,小平邦彦自然也在其中。教材,就是要绝大多数学生都能看懂,而且能学到知识的课堂用书,所以,教材的口径应该是最宽的,是可以让最多的人受益的,这就需要一个自己经历过从“不懂”,到“懂”的明白人来写。从小平邦彦的故事从得知,这位可敬的数学家在中学的时候,学习范德瓦尔登的《代数学》,学不明白,就只能抄书,后来在日本战败时的一片焦土中出道,他青少年时受过的苦,还有对数学的努力执著,足以让人感到心酸。他把他对数学精深的理解,写成了能让大多数人学懂的知识,凝铸在了他的著作之中。
前一段时间,我和一位武汉大学学金融,却爱好数学的小兄弟聊天,他在微信中说到,小平邦彦的这本书里面,宝藏不计其数,他不敢想象里面还有多少好东西,很多别的书要用大学,甚至靠近研究生的知识才能论证的知识,这本书用高一高二的知识就能解决,而且严谨而流畅,这本书的口径宽度和思想深度惊人。
比如,隐函数,隐映射,证明好直接。史济怀曾说,隐函数隐映射是初学微积分最难的,有些是用多复变知识给重新证一遍,史济怀对科大的学生说:你们读的懂就读,读不懂不做要求。但是这本书里的证明如此直接而正式而简明,借助多元积分闭区域的知识,这是人能想到的?多元泰勒还能这样用,隐函数定理就像是熟透了自动掉下来的,把严格的理论,用这样简明而严谨的方法表达,我就算读遍所有的书,都想不到这样来处理。多元偏导存在且二阶偏导连续推出交换次序二阶偏导相等再推出Young定理,再往下加上限制 推出Schwarz定理,一以贯之。
能够在一本高一学生就能看懂的书中,贯穿微积分,实分析,泛函分析,如此深刻的思想,地球上恐怕只有小平邦彦能做到。
这本书我也曾多次拿给初中毕业的学生,作为初升高的辅助教材来讲解,对于书中那些相当精彩的处理方法,有一个学生一脸崇敬的问我,老师,小平邦彦他自己是怎么想到的啊?这个问题其实我根本无法回答,我只能调出小平邦彦自己曾经说过的一段话:“对我来说,没有比数学书更难念的了。数百页的书从头到尾念完至难。因为知道‘数学’读懂了,也就成为最简单不过的事而已。所以只念定理,努力想了解它。证明就自己想。而在一般情形之下是想不透的,只好看书上的证明。但是读一两次也不觉得懂,便把证明写在笔记上看看。这回注意到证明有不中意的地方,就想有没有别的证明法?这样子好不容易读完一章时前面的部份已经忘了。没法子,又从头复习。这回倒在意起整本书章节的排列方式来。”我只能告诉我的学生,他是通过努力思考而获得的,但是,事实真的是如此吗?
我时常无端的猜想,小平邦彦应该来自于天顶星某个具有高度智慧的种群,甚至是超越我们这个宇宙时空之外的智慧种群,遥望到了我们这个世界学不好数学的人有多愚钝,于是来到我们这个世界,将他所知道的教给我们。为了让愚钝的世人能理解他的知识,他在前期不得不封印了他的知识与智慧,把自己变得愚钝,然后理解世人的愚钝之后,再把他的知识以愚钝的世人能理解的形式表述出来。
于是,我在上一篇文章中写到,“······所以,你不要认为你基础不好,也不要认为你数学思维能力不强,因为我们世人(一般的普通人)的数学基础和能力的差别,在以数学之神的形式而存在的小平邦彦大师的眼里,那就像我们看一只蚂蚁的体长是6.3毫米还是6.25毫米的差别一样,这个差别其实并无实质上的意义,而小平邦彦大师由此就为我们提供了一个适应口径最宽的学习数学的方法,那就是他在晚年,把他毕生所学倾注在一本高中生就可以看懂的解析教材上,我们只要按照正确的方法努力去读,就能读懂,而读懂之后,就会知道怎么去应用,别人能够想到的,你也能想到,甚至很多别人想不到的,你都能想到。”
从这个角度上来说,他与基督耶稣一样伟大,与特蕾莎奶奶同等圣洁。只不过,小平邦彦生性木讷,低调,谦虚,极不喜欢出风头,他太伟大了,伟大到根本不愿意去宣传自己,或者应该说是不屑。他一生都在默默的为了数学知识和数学教学而燃烧自己,就这样一位伟大的数学家,世人,尤其是数学圈外人知道他的却是真不多。直到1997年,这位可敬的数学家离世时,依然保持着低调的风格。他的葬礼没有宗教仪式, 灵柩上放着日本天皇送的花, 旁边环绕着花簇。 在他最喜爱的肖邦的乐曲中参加葬礼的数百人各自献上了一朵白色康乃馨给逝者。他完成了自己的使命,回归到天顶星去了,但是,他留下的精神财富,依然闪耀在人间,照亮着人类文明发展的道路。
在人类文明史中,有许多卓越的数学家,如牛顿,莱布尼茨,欧拉,高斯,庞加莱,柯尔莫哥洛夫······但是,他们大多高高在上,他们的理论对一般人来说,同样也是高高在上,揉一揉已经仰望得发酸的脖子和已经被光芒晃得发花的眼睛,我们同样也需要一位能直接来到我们身边的数学家,把他的知识以我们能够看懂的形式教会我们。童话中,在彩虹的尽头,有一座精巧的城堡,城堡里面住着一位善良而睿智的老魔法师,当人们历尽千辛万苦找到他的时候,就会慷慨的拿出他配制的魔药给来访者,吃了这种魔药的人,就能获得智慧。
但是我总觉得,这位慈祥的老魔法师长着和小平邦彦一样的面容,却又有着邻居家老爷爷的和蔼可亲,他不忍心人们把精力耗费在找到他的路上,他来到人间,把他的智慧魔药的做法详尽的写出来给大家看,具体的配方和工艺就在小平邦彦的书中。
种种伟大的贡献,小平邦彦已经做到了,而我只是想说到,告诉别人有这样的一本书。于是,我辛辛苦苦,呕心沥血的推广小平邦彦的《微积分入门》,从2009年年初到2019年年初,已经整整十年了,这十年中,很多人听了我的言论之后观望,这些言论也被人当成我别有用心而刻意忽略,也遇到过浅尝辄止的人,听了我的推荐之后,试着读了读,但是放弃了深入钻研的机会。这些我都不顾,终于,在上文中提到的那个武大的小兄弟不堪我的蛊惑,认真的去研读了这本书,在惊叹中给出了对这本书极高的评价,而且人民邮电出版社图灵公司也再版了这本书的修订版。编辑武晓宇多次和我交流,不耻下问,征求我的意见;市场部的李洁女士向领导申请,为我颁发了图灵公司第一例“优秀读者”的荣誉证书,在此,我深表感谢,也诚惶诚恐,因为我自认为还是德不配位的。但是我会继续把这本书品读下去,也会继续把这本书推广下去。


越战时期,代数几何教皇格罗腾迪克在越南的森林里为越南的数学工作者开讲座,这不是作秀;日本二战战败后,被遣返的侨民即使是在码头等待轮船时,依然架起黑板为孩子们上课,这也不是作秀。

开篇时提到的,长沙定王台湖南图书城,在十几年前,二楼几百平方米的卖场里面,有三分之一是高等教育的教材,目测足有上百个书柜。到现在,只在三楼的一个犄角旮旯里卖高等教育的教材了,就一个书柜,里面教材不足百本,还有些无关痛痒的科普读物;岳麓山下大学城里的新华书店,曾经有四层楼的卖场,后来变成一层楼,楼上变了旅店和网吧,再后来左边两个门面租给了考研机构做办公室,卖场只有剩下的三个门面,最近听说为了修地铁,那栋房子都拆了。八九十年代,中小学的教室墙壁上时常贴着一些很有意义也很有艺术性的宣传画,我记得有一张是在晴朗的月夜下,学生捧着书,拿着笔,在凝望着夜空思考,背景是火箭直上九霄,卫星遨游天宇,显微镜在探求细微的物质结构;还有一张是一位头发花白,带着厚厚的眼镜的老科学家,在耐心的指导拿着仪器做实验的学生。那些孩子,在我幼时的理解中,他们都会是将来的科学家,建设国家的栋梁之才,推动人类文明进步的主力军。那么,他们会不会来?他们会来吗?他们不会来吗?我想,他们还是会来的,毕竟,小平邦彦已经在这个世界来过,并且留下了他的思想。
庭有枇杷树,吾妻死之年所手植也,今已亭亭如盖矣。
——《项脊轩志》 明·归有光
关注 哆嗒数学网 每天获得更多数学趣文