原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，金星光，哆嗒数学网翻译组成员。

校对，mathyrl。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

遇见莫比乌斯带——拓扑世界中最具有“讲故事”潜力的拓扑结构。

如果你和数学家戴在一起或者去参加数学拓展项目，你很有可能会遇到莫比乌斯带。它在数学世界中是一个很特别的存在，原因在于它很容易被制作，娱乐性很强并且隐藏着一些令人吃惊的数学秘密。

你可以在自己舒适的家里，仅仅用一条纸带或者意大利面团就可以做一个莫比乌斯带。将纸带（或面团拉成条状后）一端固定，另一端旋转半周后，将两端粘到一起就可以得到一个莫比乌斯带。它看起来很像一个圆柱体，但还是有些不一样的。如果碰巧你是一个编织手的话，或许能够制作一个可以穿戴的莫比乌斯带。

我们通常使用莫比乌斯带来说明拓扑学中的可定向性。可定向性是你所熟知的但却很难被定义概念之一。我不记得有多少次我盯着我的教科书里对于“定向”的定义:“一个对于局部定向的连续选择。”我觉得这个解释毫无用处。为什么这个词的定义中还会包含这个词。

还有一个更直观的方式去理解可定向性,至少对于一个在三维空间中的二维的物体来说,空间是可定向的。如果你可以选择“向里”和“向外”或者“向上”和“向下”，来定义二维空间表面每一点的方向，并且这个方向具有一致性。你该不会用“从上到下”来定义一个相同点的方向吧？

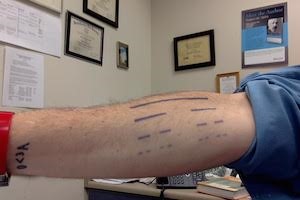
或许弄清楚莫比乌斯带最直观的方式是将一个球体、一个圆柱体和一个莫比乌斯带一起把玩。如果你拿着一个球体，在北极点处你可以宣称此点方向“向外”，指向为竖直向上。当你在球面上移动该点时，“向外”的方向仍然指向球体外部。相比之下，试着在莫比乌斯带上任意选择具有“向上”或者“向下”的点。当你沿着莫比乌斯带滑动时，最终回到最开始所选择的点，方向已经由“向上”变成“向下”了。尽管你用一张具有正反面的普通纸制作成莫比乌斯带，但此时已经失去了正反面。你可以通过直线移动，从纸的正面到背面，而不是把纸翻转过来。

在莫比乌斯带中蕴含着很多数学中的奇妙现象。一个经典的做法是将莫比乌斯带沿中间剪断，看看你能得到些什么。如果将莫比乌斯带沿三等分线剪开呢?如果你将莫比乌斯带再多旋转几个半周、结果又会怎么样呢?比起在博客上阅读，不如自己在家里验证会更有意思。

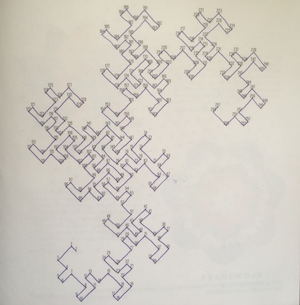
我最近才了解到到的有关莫比乌斯带的特性是六色定理。你可能听说过四色定理:任何一张地图都可以用四种不同的颜色将其涂满，并且相邻的国家颜色不同。这个定理并没有它所陈述的那样正确。我们需要指定这张地图是在球面或平面上。准确来讲，不同的表面上有不同的地图颜色定理，而对于莫比乌斯带，它是六色地图定理。

要使这个定理得到验证，首先要记住莫比乌斯带是像任何好的数学对象一样，是一个理想化的存在，它并不存在于我们混乱的现实世界中。它是二维的，不是像真实的纸张那样是三维的，因为不存在任何的厚度将它前后面分开。为了将这一观点形象化，你可以用一张透明的纸制作一个莫比乌斯带。这样，当你绘制你的地图时，你就不能在任何一点上把纸的两侧染成不同的颜色（莫比乌斯带是二维的）。如果你在一张纸上绘制地图，然后再把它折成一个莫比乌斯带，那么平面上的四色定理将会起作用。

在这里我有一张需要用六种颜色涂满的莫比乌斯带的图片。在你的电脑屏幕上可能很难看出来，最好的方式是自己在家里制作一个吧，而不是听我在这里讲！

莫比乌斯带也同样吸引着艺术家。你可以制作或者购买印有莫比乌斯带图案的围巾、吊坠和戒指，你甚至可以演奏有关莫比乌斯带的音乐。它讲故事的潜力也是很强大的：你沿着某个东西转了一圈，回到起始的地方但迷失了方向。向上变成向下，向里变成向外。或许以莫比乌斯带作为故事的创作背景，最赞的就是Vi Hart创作的感人故事啦， Wind 和 Mr. Ug，两个“似乎”永远不可能相见的朋友。

（https://www.wimp.com/mobius-story-wind-and-mr-ug/ 这是这个故事的链接视频，没有字幕但很容易听懂。整个创作是在一个莫比乌斯带上完成的，先是讲了 Wind and Mr. Ug的故事，后来是Wind 与她的a little pet dog的故事，但后来发生了地震，至于这个故事的结局还需要大家自己去制作一个莫比乌斯带去探寻哈~）

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，donkeycn，哆嗒数学网翻译组成员。

校对，小米。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

拓扑学所关注的是压缩和拉伸，而不是距离。然而无限耳环展示了拓扑学和几何学之间微妙的关系。

拓扑学有时被称为是戴上啤酒眼之后看到的几何或者是没戴眼镜看到的几何。几何学研究各种形状：它们是如何位于空间中的，它们是如何与自己以及彼此之间相互作用的。做几何通常需要用某种方式来测量距离。而另一方面，在拓扑学中，你可以毫无顾忌地拉伸或压缩；所以，在一个拓扑空间中，任意两点之间的精确距离不是本质问题。然而有时候不经意间，几何就会出现。一个数学对象的几何性质会影响其拓扑性质。

无限耳环，有时也被称为夏威夷耳环，是我在拓扑中最喜欢的例子之一，因为它展示了几何学和拓扑学之间精妙的关系。

为了构造无限耳环，你可以从一个二维欧氏平面开始：先添加一个以(1,0)为圆心，1为半径的圆；再添加一个以(1/2,0) 为圆心，1/2为半径的圆；再添加一个以(1/3,0) 为圆心，1/3为半径的圆。继续这样做下去：无限耳环由所有以(1/n,0) 为圆心，1/n为半径的圆构成，其中n取遍所有正整数。

最终，你会得到一堆嵌套着的圆，并且它们恰好只有一个公共点(0,0)。当然事情并未到此结束。思考一下无限耳环它不是什么，这是很有教益的。例如，它不同于过同一个公共点的无穷可数多个相同大小的圆组合起来（我们称之为由可数多个圆构成的楔或花束）。这一事实可能会令人惊讶，因为毕竟，我们可以用不同的压缩比例来压缩那些圆，然后再把压缩后的那些圆压到同一平面内；或者也可以从另一个方向进行转换：通过吹胀无限耳环中的那些小圆至相同大小。尽管这些转换都很平淡无奇，但这两个空间并不完全是拓扑等价的。

圆本身也是一个拓扑空间，当我们谈论无限个圆时，我们并不要求它们位于任何特定的空间中。然而无限耳环却位于一个平面内，这就影响到了它的拓扑性质。我们无法将由可数多个相同大小的圆构成的花束形状放入一个平面内，因为这些圆将以我们不希望的方式产生重叠。

证明两个空间在拓扑意义下相同是很困难的，但只要有一个拓扑性质不同就能证明它们是不同的。证明无限耳环不同于由可数多个圆构成的花束的最简单的方法是：放大某些特殊的点的周围，然后看看你能得到什么。如果两个空间是拓扑等价的，那么当你在两者对应的点附件同时放大时，你会看到拓扑等价的东西。这两个空间最特殊的点就是所有的圆的公共点，即楔点。如果我们看一看这个点周围的一个小区域，我们就会发现我们想要找的差异。

在圆构成的花束中，楔点的一个小邻域由每个圆上一点的小邻域构成。它就像一把意大利面条。（“很多”根意大利面条。）

无限耳环上的点(0,0)周围的一个小的圆邻域是欧氏平面的一个小圆。它具有某个有限的半径，且该半径大于耳环内的某些圆的半径。事实上，它比其中的无数多个圆的半径都大。所以该小圆包含了耳环内无穷多个圆。也用面食来做比喻的话，它就是有限多根条状的面以及无限多根（很小的）圈状的面。

无限耳环和由圆构成的花束之间的区别还可以以其它复杂而宜人的方式表现出来，但我想我会把它们留待以后。现在，我打算再考虑另一个异于无限耳环的空间，而这个空间也是位于一个平面内的。

如果我们是向外构造圆，而不是向内，即它们具有整数半径1, 2, 3，等等（也许我们应该称它为更大的无限耳环）。我们得到了另一个与无限耳环完全不同的空间。有几个拓扑性质可以区分这两个空间。最容易看到的是：无限耳环是有界的而更大的无限耳环不是。

这两个无限耳环之间的另一个区别是：其中一个空间是闭的，而另一个不是。平面上的闭集有几个等价的定义。其中之一是：任何与集合中的点非常接近的点都在该集合中。更大的无限耳环不包含y轴上除(0,0)外的其它点，然而随着耳环中的圆越来越大，它们看起来越来越像一条直线，所以它们越来越接近y轴。当我们取遍整个空间的无限个圆时，y轴上的每个点都非常接近更大的无限耳环上的点，但它们每一个都不在更大的无限耳环上。

另一方面，较小的无限耳环就不存在这个问题。半径为1的圆是所有圆中最大的，所以该圆限制了y轴与所有圆接近的程度。

我花了一段时间来接受这样一个事实：无限耳环与圆构成的花束以及更大的无限耳环真的是如此不同，一个空间的几何性质真的可以对拓扑性质产生这样的影响。我想，在学习拓扑的人中，不是仅有我感觉自己只是在相信别人说过的话，却没有办法把它们真正内化。但在那种时候，我会用约翰·冯·诺依曼的一句话来安慰自己：“没人能理解数学，你只能是熟中生巧而已。”

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，独行者，哆嗒数学网翻译组成员。

校对，donkeycn。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

铺满空间的曲线，一张在空间维度中具有跨越维数的谜图，他有着惊人的现实应用。

停下来看看这个独特的现象吧。想看一条能铺满空间的曲线的图像？看吧，就在下面！

啊，你一定会认为我是个逗比吧！一条可以铺满空间的曲线就好像说：一条线可以乱画，然后弯折便能铺满一个2维的区域，在这个例子中便是一个正方形。（同样地3维，4维空间的曲线也是如此，一条线可以铺满你所给的空间！）

铺满空间的曲线在他们的完整形态上并没有什么特别的特征。你可以从黑色实心正方形中学到什么？相反地，就像其他的分形，我们通常可以认为铺满空间的曲线可以是一个有限步的构造的无限版本。

有多种利用迭代来构造铺满空间的曲线的方法，这里是其中一种的动画版本（其实是希尔伯特曲线）。

在每一步，线中的每一段都被一个四段的折线所替换。这个过程中的每一条曲线都不能铺满整个空间，然而如果我们想象一下，这个过程要是可以一直持续下去，那么最终我们得到的那个无限版本就可以铺满整个空间了。

铺满空间的曲线挑战了我对维度的直觉。一条铺满空间的曲线就是一条直线的像，这一普通的一维对象，却可以铺满整个平面，这一普通的二维对象。这感觉就像是一个规规矩矩的函数，就不应该把一个一维的东西“映成”一个二维的东西一维便是一维，二维就是二维，两者毫不相干。不过还好，它只存在于无穷的情况，只是仍然有些让人不安。

（如果你正在学拓扑学课程，你可能会非常紧张。线和平面是拓扑上是不等价的，但是一条铺满空间的曲线却是一个连续的函数，他将线“映成”平面。这是怎么回事呢？难道，数学根基的错误被我们发现了？）

很难想象这种如此抽象化的弯曲程度近乎无限的线会在现实世界中有什么联系。但是事实上，充满空间的曲线让一维空间“映成”二维甚至多维空间的方法在数据处理中有许多现实应用。在这个非常奇妙的视频中，Grant Sanderson解释了一种能充满空间的曲线，希尔伯特曲线，是如何帮助我们寻找到一种最优的途径将一个图像的二维可视化数据转为一维声音数据。（B站传送门：https://www.bilibili.com/video/av4201747/index_2.html#page=1）

如果你想在自己的电脑里实现，这里有许多方法生成你自己铺满的空间曲线。如果你想投机取巧的话，只需要涂满一些方块。如果你对如何实现使用迭代方法来构造铺满空间的曲线，你可以遵循Vi Hart的方法来画龙形曲线，而Andrea Hawksley（她的灵感来源于Kyle Calderhead）将帮助你编织一条属于你自己的以希尔伯特曲线为图案的毛毯。

对于我而言，我在一本以数学为主题的绘本《Patterns of the Universe》中寻找到了属于我自己的铺满空间的曲线的奥妙。在他们的书里，有两页画了铺满空间的曲线。一条是在封面上显示出来的，而另一张则在下面，是用线将点连起来的图形。

在这个星期的前半部分，我一直驳斥着一些人对数学教育的错误观点，而此时给一条舞动的蛇上上色就能使我的心归于平静。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，radium，哆嗒数学网翻译组成员。

校对，sanshi。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

在拓扑空间中，拓扑学家的正弦曲线的经典在于它连通但非道路连通，即你可以看到他的终点线，但你不能从这里跑到那里。

分析和拓扑的学生初看这个集合有四个基本的性质：开区间、闭区间、紧的以及连通性。在前面的这些性质中似乎连通性是最简单的。

连通这个词语的解释很好理解，但在数学中要严格地定义却出奇的困难。拓扑学家的正弦曲线就是众多例子中的一个，这个例子可以明确的说明连通的含义。

在通常词典里，我们通常认为连通是两个物体之间的性质:A和B如果以某种方式重叠或者你可以从A连到B那么我们说A和B是连通的。在数学里面连通性是一个集合的性质。那么我们如何让自然语言的思想数学化并应用它？一个似乎很理所当然的定义是，如果你可以从集合中的一点到集合中的任意一点那么我们称之为连通。但是如果是联排公寓又如何呢？

在联排公寓中，你可以从一个房间到同一单元的另一个房间，但如果你不离开联排公寓你就不能从一个单元到另一个单元。那么联排公寓楼连通么？我想应该是连通的。所以这不是连通的正确定义。能够在集合中从任意一点到另一点是一个非常有用的数学性质，但是这个性质太强了。数学家称这样的空间为道路连通，稍后我们会仔细讲讲它。

连通性是一个很微妙的东西，我们再次尝试着定义如下：一个集合X是连通的，如果你不能粘贴一子集在某个非空子集A中，而剩余的部分在非空子集B中，以至于A、B不相交。这里有一个小问题:这样的定义可能会完全失效，因为这会让太多的空间分裂。我们可以将所有实数集分裂成这样的集合：大于等于0，小于0。它们不相交，因此以我们的定义实数轴是不连通的。很明显通常的实数轴因该是连通的但是这样的定义让它不连通了，所以，这就错了。

问题在哪里呢？我们将分界点包含在一个集合中而没在另一个集合中。如果我们让两个集合同时包含分界点，集合将会相交；如果两个集合都不包含分界点，集合将不会相交，但是这两个集合也就不能覆盖实轴上所有的点。“正确”的答案是从两个区间中排除端点。 区间不包含它的端点我们称为开的。所以我们说集合X是连通的，如果你不能做到粘贴某一子集在非空开子集A中，而剩余的部分在非空开子集B中，且A、B不相交。

这个定义不仅仅在一维集合中成立；我们也可以在更高维定义开集。基本上，一个集合是开集如果这个集合中没有任何一个点位于边界上，或者等价的定义，如果集合中每一个点都存在完全包含在集合中的一个小邻域那么这个集合为开集。

下面是拓扑学家的正弦曲线的一部分，注意到图形的左边部分实际上并没变成实心的。这只是由于用有限的常识去理解无限的结果。图像由Morn the Gorn提供，维基共享资源。

这个空间是函数 f(x)=sin(1/x)在(0,1]区间加点(0,0)的图像。我们可以看见随着x接近0,1/x越来越大，所以sin(1/x)在-1到1之间剧烈震荡。拓扑学家的正弦曲线是数学系学生看到的第一个例子，它连通但非道路连通。你可以看见他的终点线，但你不能从这儿到那儿去。

为什么连通？让我们尝试着将它分到两个不相交的开集。其中的一个集合包含点（0,0）因为是开集，它也包含以（0,0）为中心的领域内。无论多么小的领域内它都将包含一些x正半轴的点和在y轴上的0点。也就是说着它将包含一些f(x)的图像。这就意味着如果我们想要分裂空间我们不得不将函数f(x)的图像的一部分分到一个集合，而剩下的部分分到另一个集合。但是这儿没有办法分裂这个图像，是连续的曲线，就像实轴一样是连通的。

那为何拓扑学家的正弦曲线不是道路连通的呢？假设你正尝试着从 f(x)图像上的一点到(0,0)点，你将会一直走，走到永远。你会真的真的很接近它，但总会有一条无限长的路还在你面前。

一个密切相关的空间是封闭的拓扑学家的正弦曲线。一个封闭的空间包含所有边界点，边界点意味着可以任意接近集合里面的点。随着曲线f(x)震荡，所有在y轴上-1到1之间的点越来越接近曲线上的点，所以为了使拓扑学家的正弦曲线成为闭集，我们也在y轴上划分一个-1到1的线段，作为边界。这样不会破坏其他的拓扑性质——它依然连通但非道路连通——但是现在也封闭了。有些人喜欢玩这样玩儿。

如果你之前学过拓扑学，你可能看到过一条称做紧致性的拓扑学性质的定义：一个集合是紧致的，如果每一个开覆盖都有有限子覆盖。拓扑学家的正弦曲线不是紧致的，但是封闭的拓扑学家的正弦曲线却是。本着挫败数学教科书的精神，我将为读者留下一个思考题：找出拓扑学家的正弦曲线的一个开覆盖但是没有有限子覆盖，然后指出为什么这例子在封闭的拓扑学家正弦曲线中不成立。在一个闭，不可数，无处稠密的[0,1]区间的子集之后写下你的答案，然后送到康托广场，Log2(3)邮箱

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

作者，小米，哆嗒数学网翻译组成员。

A drunk man will find his way home, but a drunk bird may get lost forever.  —— Kakutani

醉鬼总能找到回家的路；但是喝醉了的鸟儿可能永远回不了家。 —— 角谷静夫

今天我们要谈的是一个概率论中的重要结论：Z^d上的随机游走当d≥3时是非常返的，而当d=1,2时是常返的。

Z^d在这里表示由d 维欧氏空间中全体整点（即坐标全为整数的点）构成的集合。想象有一只青蛙以秒为时间单位在Z^d上做随机游走，那么它将按如下规则运动：在初始时刻（记为第0秒），青蛙位于原点；在每一秒钟，青蛙都会等概率地跳到某一个与它上一秒所在位置相邻的整点。由于Z^d上的每个整点都有2d个邻居，因此这个概率也就是1/(2d)（见下图)。

我们这里介绍的随机游走看似一个简单的数学模型，其实它的应用十分广泛。最常见的例子有物理学中布朗运动，金融市场中股票价格波动等等。

那么我们的问题就是，既然青蛙一开始位于原点，那是否总存在一个（随机）时刻T，使得第T秒时青蛙又回到原点呢？如果是，那么我们就称这样随机游走是“常返”的，否则就称是“非常返”的。

事实上，我们总可以假设存在一个介于0和1之间的实数p，它就是青蛙回到原点的概率。仔细想想，其实p的存在性本身也是不平凡的，因为我们知道古典概率论中，事件的概率只涉及到有限个变量，而这里回到原点的行为却与青蛙在无穷时间内的行为有关。当然，在公理化概率论中，通过建立起合适的概率空间，我们可以说明这样的p是存在的。这样，我们通过引入p，判断常返性就转化为判断p是否等于1的问题了，因为“总能回到原点”用概率论的语言来说就是“以概率1回到原点”。

下面我们来看随机游走另一个有趣的性质：马氏性。我们注意到，对于任意给定的时刻，比如第100秒，第100秒后的青蛙的位置只取决于第100秒时青蛙的位置，而前100秒的时间里，青蛙如何跳到这一位置方式无关。这就是所谓的“马氏性”，即给定现在，未来和过去独立。随机游走还具有“强马氏性”。所谓“强马氏性”，是指可以把前述的“第100秒”换成任意“只取决于历史的随机时间”（这样的时间又叫停时）。比如我们定义T成为青蛙第一次回到原点的时刻，那么T就是一个停时，并且关于T的强马氏性可以这么理解为：在随机时间T之后发生的事情，与在随机时间T之间发生的事情无关，因为我们知道在第T秒，青蛙又回到原点了，所以在时间T后开始的随机游走与一开始从原点出发的随机游走将遵循同样的规律。

如果要解释什么叫“只取决于历史”，不妨看一个买卖股票的例子。比如说你今天想卖出一只股票，你当然希望可以在一天当中最高价的时候卖。但很遗憾，除了碰运气，这是不可能做到的，因为除非一天已经结束了，没人能知道股价什么时候位于最高点。相反，如果你的策略是，“如果股票价格位于过去12个小时内的最高点就卖出股票”，那这就是一个可行的策略。后面这个策略中的交易时间就是一个“只取决于历史”的随机时间，也就是停时，而前者“一天当中的最高价”则不是停时。

如果你没看懂上面一大串关于马氏链和停时的描述，没关系，你一定也可以直观地理解以下结论。如果从原点出发的青蛙以概率p会回到原点，那么青蛙一定会以概率p^2(p^n表示p的n次方，下文相同)回到原点两次，这是因为，青蛙回到原点两次＝青蛙回到原点1次＋青蛙从原点出发再回到原点1次。由强马氏性，拆分后的第二个事件的（条件）概率也是p；因此，青蛙回到原点两次的概率就是p^2。同理，青蛙会以概率p^3回到原点3次，以概率p^4回到原点4次，等等。如果我们把青蛙回到原点的总次数记为N，那么上面的计算表明P(N≥k) = p^k，也就是说N是一个服从几何分布的随机变量。当p=1时，上述论证依然成立，只不过我们得到的N是一个取值恒为+∞的随机变量。

于是，根据几何分布的期望公式，我们得到了N的期望为EN = 1/(1-p)；同样地，当p=1时，该式理解为EN=+∞。因此，EN是有限还是无穷，就刻画了随机游走是否常返。

我们还可以从另一个角度来计算EN。令X(n)为第n秒青蛙所在的位置，而an是取值0和1的随机变量，其中a(n)＝1当且仅当X(n)=0，即a(n)＝1当且仅当第n秒青蛙位于原点。根据定义我们得到N是全体a(n)的和，也就是N=a(1) + a(2) +…+ a(n) +… 这是显然的，因为整个数列(a(n))中有多少个1，就代表青蛙返回了多少次原点。

当我们对以上无穷和式取期望，并根据期望的线性性，交换无穷求和与求期望的顺序（这里能够换序是因为涉及的项an都是非负的，因此满足换序的条件），我们得到

EN = E(a(1) + a(2) +…+ a(n) +…) = E a(1)  + E a(2) +...+E a(n) +...

等等，E a(n)  是什么呢？根据定义，E a(n) = P(X(n)= 0)，正是第n秒青蛙恰好位于原点的概率！计算这个概率就是一个组合问题了，而判断常返性则变成了一个判断无穷级数敛散性的问题。

记A(n)= E a(n) ＝ P(X(n)= 0)。下面我们的目标就是对A(n)进行估计，并由此判断无穷级数∑A(n)是否收敛。

在一维(d=1)时，如何计算An呢？注意到每一秒钟青蛙必须向左跳或者向后跳。因此在第n秒回到原点的必要条件就是n为偶数。而当n为偶数时，青蛙必须恰好有n/2的时间向左跳，有n/2的时间向右跳，才能在第n秒回到原点。我们知道每秒钟青蛙向左和向右的概率都是1/2，那么利用组合数公式，我们就得到

 
对于阶乘，斯特林公式给出了渐近公式：m! ∼(m/e)^n·sqrt(2πn) （sqrt表示开二次根号，下同）。代入A(n)的表达式，我们得到A(n)∼1/n·sqrt(2/π)这个渐近关系当然只限于n为偶数）。微积分中熟知的结论是p级数∑1/n^p收敛当且仅当p>1，否则发散。于是我们得到∑A(n)在d=1时发散，也就是说一维随机游走是常返的。

如果我们在高维时采用类似的方法，就能得到A(n) ∼ c· n^(-d/2)，其中c是与d有关的一个常数。同样再借助p级数的知识，就能得到当且仅当d/2 > 1时，也就是d ≥3时，随机游走不常返；相反，d=1，2时，随机游走常返。

为了避免复杂的组合数估计，我们也可以从另一个简单的事实中看出A(n)的阶就是n^(-d/2)。如果我们令y(n)=X(n)-X(n-1)为第n秒时青蛙的位移，容易看出所有y(n)都是独立同分布的随机单位向量。由中心极限定理，Z(n) :=X(n)/sqrt(n) = (y(1) + y(2) + … y(n))/sqrt(n)将趋向于一个d维正态分布Z。那X(n)=0意味着什么呢？由于X(n)只能取整点，那么X(n)= 0表明Z(n)的取值大约位于原点附近一个边长为的1/sqrt(n)小正方体中。根据中心极限定理，Z(n)的取值落于这个小正方体中的概率与Z是差不多的，而对于后者，这样的概率恰恰就约等于小正方体的体积，(1/sqrt(n))^d（注意到是d维空间），乘以原点处Z的密度函数大小，一个非零的常数。这样我们就很容易得到了A(n) ∼ c· n^(-d/2)这个结论。

如果要把这个随机游走的小结论用于生活中，我们也许会为再也不用担心认不得路而感到欣慰，因为二维随机游走是常返的，就算是不认识路随便乱走，也总能到达任何想去的地方！当然这句话既对也错；对的地方在于，由常返性，确实总存在一个时间T，在平面上随机游走的你也能走到任意想去的地方；错的地方在于，更进一步的理论表明，这个随机时间T是一个期望为无穷的随机变量，也就是从平均的意义上说，你永远也到不了目的地！

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者，Evelyn Lamb，数学及科学普及自由作家

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，e^iπ+1=0，哆嗒数学网翻译组成员。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

上回我们写了一篇关于康托集的文章，它是一个将小与大统一起来的有趣的数学空间。

说小是因为它的长度只有零，但是说大是因为它本身是个不可数的集合。

一旦一个数学家着手处理一个数学对象，直觉上第一步便是试着摆弄它，然后看看会发生什么。这使我们得到了胖康托集（编者注：Fat Cantor Set 正规教材上译为类康托集，但是本文要显示他比康托集“肥硕”于是就这样翻译了）。

当有人提起康托集时，他们指的是标准三分康托集，也就是我之前提到的那个康托集。

这个集合的构造是通过将区间[0,1]中间三分之一的部分移除，只留下区间[0,1/3] 和 [2/3,1]。

然后将剩下的每个区间再去掉各自的中间三分之一，这样的操作一直重复下去。

令人惊奇的是，这样的操作使得这个区间还有一些东西留下，却没有长度。

而被移除的区间长度总和是1，而这就是原来区间的长度。

第一个能想到的符合逻辑的操作就是将康托集移除三分之一这个比例换成其他的比例。

如果我们只移除每个区间中间的四分之一会产生什么样的结果呢？

我们同样从区间[0,1]开始操作。

第一步，我们只留下区间[0,3/8] 和 [5/8,1]。

然后我们继续移除每个区间中间四分之一的区间（移除的区间长度变为3/32）。

你可能会认为会有更多的东西被留下，因为我们每步移除了更短的区间，但这个想法是不对的。

如果你将所有移除的区间长度都加在一起，我们仍旧得到1。

这个康托集实际上并没有比我们之前那个集合更有趣。

当然我们也没有变得更不幸运。

如果我们保证每次移除区间所用的比例都是一样的，那我们总能得到移除的区间长度总和为1。

当然有很多方法区别那些移除中间三分之一，四分之一，或者任何一个比例的康托集，但是现在我们准备试着对康托集做很不一样的操作。

第二件我们可以做的事情是改变每次移除区间时所用的比例。

我们将再次从区间[0,1]中移除中间四分之一的区间，这样我们留下区间[0,3/8]和[5/8,1]。

但是到了第二步，我们将从每个剩余的区间中移除它中间一个长为十六分之一的区间。

这时候，情况已经发生了些许变化。

之前的时候，我们从每个剩余区间移除了长为三十二分之三的区间，这比起十六分之一稍微长上一些。

在新的构造中，我们将不断改变每一步里剩余区间需要去除的区间长度。

在第一步中，我们移除了初始区间的四分之一。

在第二步中，我们从每个剩余区间移除长为十六分之一的区间，相较于初始区间，共移除了八分之一。

在第三步中，我们每个剩余区间移除了长为六十四分之一的区间，相较于初始区间，共移除了十六分之一。

我们可以继续这样的操作，到了第n步的时候，我们将移除整段区间1/2n+1的长度。

如果这个步骤无限地做下去，我们总共移除的长度将会是1/4+1/8+1/16+…，而它的和则是1/2。

这时候我们的确得到了一些新的东西！

这个结构被称作史密斯-沃尔泰拉-康托集合，或者是胖康托集。

康托集的一维测度是0，这是因为我们移除的区间长度和等于一开始的区间长度，但是胖康托集还留下了一些东西——从整个[0,1]区间里留下整整一半。

那这些是从哪里来的呢？

根据构造过程，胖康托集不包含任何区间。

每当我们看到一个区间，我们都要移除这个区间中的一部分。

某种程度上，有一些长度是被留下了，但不是以我们熟悉的方式留下的。

如果我们试图用手去抓，只能抓到一把灰尘。

康托集挑战了我对小与大的直觉认识。

胖康托集更将我的直觉完全吹散了。

一个没有任何微小片段的一维物体究竟是怎样获得一定长度的？

当然，这样说其实不完全公平。

在区间[0,1]上的所有无理数组成的集合，它的一维测度为1，长到居然与整个区间一样，但是这个听上去并没有那么的违反直觉。

无理数无处不在。

所以，你在数轴上随便一扫，都能扫到无理数。

在数学上，我们把这种情况叫做区间上稠密，或者在所有实数构成的集合中，无论怎么样选择一个子区间，无论有多小，都会包含着无理数。 

是否稠密这一问题使得胖康托集变得更奇怪。

胖康托集在[0,1]区间上不是稠密的，而且他们甚至在任何更小的区间上都不是稠密的。

无论你的区间取得多么小，你都能找到一个完整的区间，其中任何一点都不在胖康托集中。

我们将这种情况叫做无处稠密(nowhere dense)。

这样胖康托集的长度是1/2就没什么稀奇的地方了。

事实上，调整每一步需要移除的区间长度，我们可以得到一个按照我们想要的任意长度的康托集。

我们不能得到一个长度为1的胖康托集，但是我们可以得到一个长度趋近于1的胖康托集。

无论我们将胖康托集塑造的多大，他们都不会占满任何一个区间，并且会无处稠密。

那我们可以在哪里看到他们呢？

我第一次遇到康托集的地方就是康托函数，这我提到过了。

康托函数，或者说是魔鬼的楼梯，向我们展示了联系了微分与积分的微积分基本定理的局限性。

事实上胖康托集也能做到这一点。

特别地，意大利数学家沃尔泰拉 (Volterra ,1860-1940)利用胖康托集构造了一个可微函数但是导函数不可积。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，金星光，哆嗒数学网翻译组成员。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

康托尔集很庞大，但它当中几乎不含有任何“内容物”。

上个月，我写了关于π-Base网站的一些文章，这个网站与《拓扑学中的反例》这本书起着相似的作用。碰巧这学期我教授拓扑学这门课程，因此去回顾这些有价值的反例是件有趣的事情。作为博客上的一个新系列，我将会写一些看似怪异但不乏趣味性的数学空间的文章。我们就以康托尔集开始吧，这个有用的空间一直活跃在全世界的数学领域中。

通常有两种主要的方式来思考和理解康托尔集，我们先以第一种比较有趣的思考方式开始吧。我们先画出一条从0到1的线段，并且包含端点，因此我们得到闭区间[0,1]。现在我们将这个区间三等分，去掉中间的开区间(1/3,2/3)，然后我们就会得到[0,1/3]和[2/3,1]这两个闭区间。接着我们分别从中间去掉[0,1/3]和[2/3,1]这两个区间中间的1/3，我们就会得到[0,1/9]、[2/9,1/3]、[2/3,7/9]和[8/9,1]这四个区间。如果我们按照以上的方式继续做下去的话，我们就会得到康托尔集。

可能稍微令人惊奇的是，当你继续上述的所有步骤之后，几乎没有什么东西剩下。但是如果你进一步的思考，你将会发现0 , 1/3 , 2/3 , 1以及子区间的端点并没有被去掉。更令人惊讶的是，不仅仅是这些端点，还有非常多其他点, 因为端点数量只有可数个，但是整个康托尔集却是个不可数的集合。想要弄清楚原因，就让我们以另一方式来重新思考康托尔集吧。 

第二种描述康托尔集的方式虽然有些枯燥但会更加精确。我们通常以十进制来书写数字，但除了这种书写方法以外我们还可以以三进制来书写数字，这就意味着我们只需要数字0、1和2就可以了（十进制书写的1到10如果以三进制来书写就会写成1、2、10、11、12、20、21、22、100、101）。康托尔集是闭区间从0到1的数字中，那些在三进制中仅用0和2书写的数字的集合。例如，0是包含于康托尔集中的，至于1可以被写成0.22222....(就像0.9999...=1那样)。

用三进制的方式来思考康托尔集特别自然地符合康托尔集的构造。将闭区间[0,1]中的所有数字用三进制转换。当你去掉区间(1/3,2/3)，你就同时在去掉这个集合中三进制小数中第一个小数位为1的点。当你去掉剩下区间的1/3，你就同时在去掉三进制小数中第二位小数为1的点，以此类推。但我们确实要对端点值小心。早期的时候，我们注意到数字1可以被写成1或0.2222...类似地1/3可以被写成0.1或者0.0222222...。任何用三进制书写的数字如果以1收尾都可以用2的无限循环来代替，康托尔集是三进制中仅用0和2表示的数的集合，但这并不意味着这个集合中的所有数字一定要按照这种方式来书写，因此我们允许1、1/3以及诸如此类的数字成为这个集合中的一部分。

康托尔集并不仅仅是一个可以纹在身上的炫酷的事物，它也拥有许多很好的性质出现在早期的拓扑学和分析学的课堂上，你也可以用它来测试一些拓扑学和分析学中的一些新的定义。它将“大”和“小”的特性有趣的结合到一起。我在前文提到康托尔集是个不可数集。在去年夏天我写过一些有关不可数集合的文章。可数集的定义依赖于集合中的元素可列，即使我们不能写下整数集所有的元素，但是我们能够想出一种方法去列出它们，知道每个整数将会出现在数列中的哪个具体的位置上，因此整数集是可数的。令人吃惊的是，一些看似很大的集合依然是可数的。最令我吃惊的要数有理数集啦，有理数集理应要比整数集“大”，但准确来说，有理数集与整数集具有相同的元素个数。

实数集是不可数集。这意味着任何我们想要列出这个集合所有元素的方法都将以失败告终。康托尔的对角化论证，完美的证明了这一点，这是我最喜欢的数学证明。同样的方法可以证明康托尔集是不可数的，事实上它与实数集的元素个数相同。

这就是康托尔集开始成为反例开始的地方。它是不可数的，但它也没有包含任何“内容物”。它的长度是零。一种方法去注意到这一点是在于你每一步都去掉剩下某个区间长度的1/3.第一步，你去掉闭区间[0,1]这个区间长度的1/3，第二步你又去掉剩下区间长度的1/3，总共去掉了2/9.你去掉的长度总和是1/3 + 1/3 × 2/3 + 1/3 × 4/9 + 1/3×8/27 + …很容易的计算出这个几何级数的和为1。而这个区间的长度为1，我们去掉1个单位长度，最后却得到了多达整个实数数量的康托尔集。

如果你想要了解更多有关康托尔集的知识，π-Base列出了很多它的拓扑性质：它是紧致，完全分离，拓扑完备，非无核集(无核集定义：非空闭子集必有孤立点——编者注)。Cut-the-knot math有更丰富的有关康托尔集的知识，Robert Vallin(上述图片中有康托尔集纹身的人) 写了一本有关康托集的书。祝大家阅读愉快！

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa