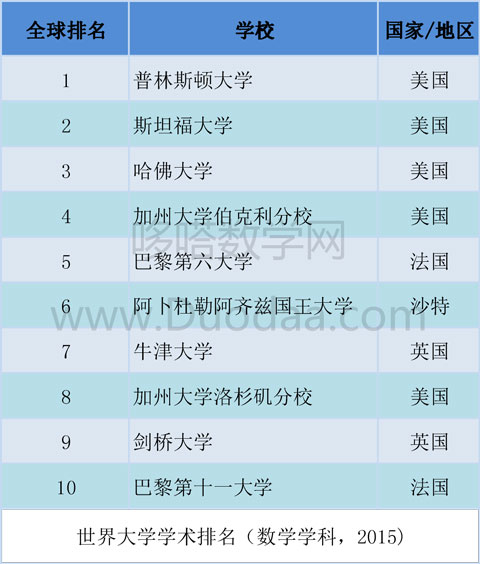
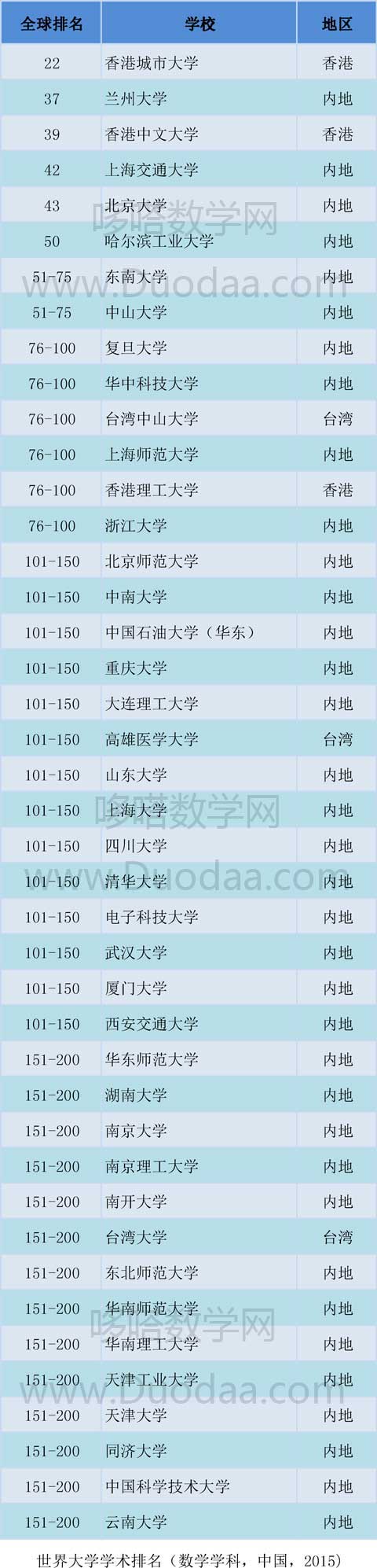
什么是代数?
关注微信:DuoDaaMath 每天获得更多数学趣文
作者,基斯·德夫林,斯坦福大学教授 ,原文《What Is Algebra》。
翻译,Aria,哆嗒数学网翻译组成员。
我们常常听人说小孩子在中学阶段掌握代数是如何如何重要,但是代数到底是什么,她又是否真如人们声称的那样重要?为什么这么多人觉得代数很难学?
要回答这些问题可比回答一道常见的代数习题要容易些,令人吃惊的是,几乎没有人能给出满意的答案。
首先,代数并不是“字母的算术”(Aria: 其实译者在中学就是这么认为的)。在最基本的层面上,算术和代数是思考数的问题的两种不同的方式。(我必须强调这篇文章中我注重的是学校里学习的算术和代数,数学家通常用这两个术语来表示某些更一般的概念。)
让我们从算术说起。她本来指的是用加减乘除四则运算来计算各种数值问题,是数学中最古老的部分,起源于大约一万年前的苏美尔(大概就是今天的伊拉克)。苏美尔社会已经达到了用钱衡量财富和进行商品交易的阶段。其他的货币象征最终让路给了黏土片上抽象的划刻(现在我们认为这是最早的数字)。时光流逝,这些符号逐渐获得了她们自身的意义:数。换句话说,数字起初是以钱的形式产生的,算术则是一种货币贸易的方式。(Aria: 今天的状况其实也差不多是吧...)

需要注意的是,数数使数字和算术的使用提前了数万年。骨头上的刻痕证明人们至少在三万五千年前就开始数数了(大多是数家人、动物、季节、财产等),人类学家认为他们刻下的就是今天称为"数据记录"的东西。但是这些古人没有数字,也没有任何证据说明他们有任何算术。这些刻痕自身只是记录,它们直接代表着这个世界上的事物,而不是抽象的数。
此外,算术并不必像学校里教的那样,用符号的操作来完成。现代的方法经历数个世纪才发展起来,在公元千年前半年在印度出现,在后半年被阿拉伯语系的商人所接受和采用,直到13世纪才传入欧洲(因此这种算术现在的名字是“印度-阿拉伯算术”)。在采用这种以符号为基础的印度-阿拉伯算术之前,商人们用一种非常复杂的手指计数或者计数板(板上画有线,线上有可以移动的小珠子;Aria: 听起来跟算盘有点像)来进行运算。算术书上描述了如何用文字进行计算,直到15世纪,符号操作开始成为主流。
虽然许多人觉得算术难学,但我们大多掌握了这项技能,或者在足够的练习下至少没有挂科。我们之所以能够学会她,是因为算术大厦的基础材料——数字,在我们的周围很自然地出现:当我们数东西、测量、买东西、做小制作、打电话、去银行、查看垒球赛的比分等等。数也许抽象些——你从没看见过、感受过、听到过、闻到过数字“3”——但是数字和我们生活的世界里真实的事物紧密地联系着。
至于代数,你的思维必须进一步脱离我们的日常生活。在代数中你学着去打交道的"x"们和”y”们表示的是数字,不过这是一种广义的“数”而不是具体的数。人的大脑并不会自然而然地适应这种程度的抽象,要做到如此,需要相当一些努力和训练。
你必须认识到,代数是一种思维方式,并且和算术的思维方式不同。那些带着x和y的公式和等式,仅仅是在纸上体现这种思维的表示。她们表示着代数,这并不比用一纸音符表示音乐来的高明。不需要符号就可以做代数,好比你不必熟练地读谱也可以演奏乐器。
事实上,商人和其他有需要的人,在符号形式被推广的16世纪前,已经使用代数长达3000年(这种早期的代数被称为rhetorical algebra"文辞代数",区别于今天通用的符号代数)。这里有几个帮助你理解算术和(学校里学习的)代数的区别的方法:
♢ 首先,代数涉及逻辑的思维而不是数值的
♢ 在算术中,你“使用”数的计算来思考;在代数中你用“关于”数的逻辑来思考
♢ 算术包括数的定量推理;代数包括数的定性推理
♢ 在算术中,你用已知的数来计算另一个数;在代数中,你引入了未知数并且用逻辑来确定她的值
上述的区别应该能让你更清楚地认识到,代数不是用一个或者更多的字母表示已知或者未知的数来做算术。
比如用一元二次方程求根公式来计算一元二次方程的根,这不是代数,这是算术。
相反地,首先推导出一元二次方程求根公式却是代数。用标准的配方法和因式分解而不是公式来解二次方程也是代数。
当学生开始学习代数,他们无可避免地用算术的思维来解决问题。考虑到他们曾经为学习算术付出的苦辛,这很自然,并且他们一开始他们遇到的代数题也是相当简单的(这是对老师而言的),这种方法也的确管用。
事实上,一个学生的算术思维越强,在代数中他可以用算术走得更远。例如,许多学生可以用简单的算术解二次方程方程: x²=2x+15,完全不用代数。
奇怪的是,或者仅仅是看起来如此,那些更优秀的学生认为代数更难学,因为对于代数学习来说,除了最基本的题例,学生必须要放弃算术思维,然后才可能开始用代数来思考。
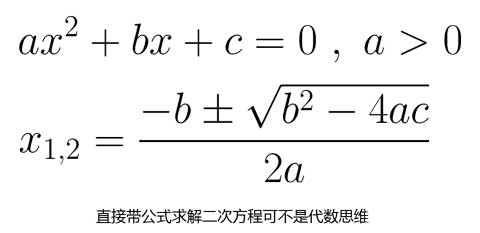
值得花这些精力去掌握代数思维吗?当然了——我相信在你历经艰辛地掌握了多数学校代数课本上的知识后,你会得出这个结论的。当今世界,大多数人的确有必要掌握代数思维。比如,如果你想要在像微软的办公软件EXCEL这样的电子表格里编写一个宏来计算格子里的项目,你需要代数思维。仅仅这个例子就能清楚地说明为什么代数而不是算术,现在是学校数学教学的一个目标。在一张电子表格里,你不用做算术,计算机自己会做,而且比人算得更好更快。使用者真正需要做的是,首先创建一个电子表格——计算机并不会帮你做这件事。
不管你的电子表格是用来计算体育比赛的比分、追踪你的财务、运营公司或者俱乐部、或者计算你魔兽世界(暴雪公司出品的网络游戏,曾经拥有最多的玩家,在中国由网易代理)里角色的最佳装备,你都需要代数地思考如何建立你想要的东西。这意味着你必须使用广义的数而不是具体的数。
当然,代数的需求并不能让学习代数变得简单——即使我认为比起火车出站和游泳池的放水问题(我们这代人做的题),电子表格对于今天的学生来说是更有意义和一个不错的应用。在如今这样一国生计依靠科技领先的世界之中,让我们的学生拥有世界所要求的思维是非常重要的。学会使用计算机正是这些技能中的一个。然而使用计算机来计算要求使用者的代数思维。
关注微信:DuoDaaMath 每天获得更多数学趣文