原文作者：Mark Levi，宾夕法尼亚州立大学数学教授。

翻译作者，daydgi，哆嗒数学网翻译组成员。

校对：Math001

关注 哆嗒数学网 每天获得更多数学趣文

我想描绘一个流体静力学“计算器”，用它可以解出任意阶多项式方程的正实数根。来做一个思想实验，我们从一片不计重量的泡沫板上剪出如图1的形状。其中第n个图形代表着当它被浸入水中的深度为x时，体积为x的n次方，在这里假设所有的薄片厚度都是1。在图2中可以看到我们的“计算器”由一根上面标着“原点0”的轻质杆（重量不计）组成。代表每一个单项式的泡沫板可以被固定在杆的任意位置；不同的是，常数项x0=1用一个可以滑到任意位置的单位重量小滑块代替。

    举个例子，我们来解下面的方程（1）：

ax³−bx²+cx−d=0,   

其中系数a,b,c,d皆大于0。这里的系数和它前面的符号共同决定了每个单项式泡沫板在杆上的位置，如图2。因为常数项小滑块不受浮力而受重力，所以它遵循相反的规则:d前面是负号，所以把它放在0的右边。

    准备好了“计算器”，我们水平地拿着杆子，慢慢浸入水中，直到用手保持杆的平衡所感受到的力矩变为0为止，也就是说，直到我们的“天平”可以自己平衡为止。这时的深度x就是方程（1）的一个根。

为了理解这个方法是怎么有效运作的，注意多项式ax³−bx²+cx−d=0,  就是所有作用在杆上的合力矩（如图3）。因此当一个特定的深度x使力矩为0时，也就意味着x是满足方程（1）的一个根。

当然，以上的方法适合任意阶的多项式，不足的是这个方法只能得到方程的正实数根。

关注 哆嗒数学网 每天获得更多数学趣文

关注 哆嗒数学网 每天获得更多数学趣文

据国际数学奥林匹克官方网站消息。在英国巴斯举办的第60届国际数学奥林匹克竞赛刚刚公布成绩，中国队以227分，六位参赛者全部获得金牌的成绩获得团体总分第一，这是继2014年后，时隔五年，中国重获第一。

最强对手美国队也以同样的227分，六位选手全部金牌的成绩获得团体总分的并列第一。这是美国队在过去五届比赛中获得的第四个总分第一。 国际数学奥林匹克竞赛是世界上最大规模的中学生国际交流活动，每年举办一届，有100多个国家参与此活动。成绩上，中国队曾经是此项赛事的霸主。2014年后，美国队实力增强，成绩提升。中国队虽然仍然是前三的强队，但更多的扮演冲击者的角色。获得此成绩，十分不易。

最后，祝贺中国队，祝贺中国队的队员。

人生漫漫长路，imo金牌也许只是一个新的起点。

关注 哆嗒数学网 每天获得更多数学趣文

作者，Radium，哆嗒数学网群友。

关注 哆嗒数学网 每天获得更多数学趣文

数学中最有诗意的定理莫过于蝴蝶效应了。美国气象学家洛伦兹1963年在一篇论文中分析了这个效应。最常见的阐述是“一只南美洲亚马逊河流域热带雨林中的蝴蝶，偶尔扇动几下翅膀，可以在两周以后引起美国德克萨斯州的一场龙卷风。”其原因就是蝴蝶扇动翅膀的运动，导致其身边的空气系统发生变化，并产生微弱的气流，而微弱气流的产生又会引起四周空气或其他系统产生相应的变化，由此引起一个连锁反应，最终导致其他系统的极大变化。他称混沌学。用MATLAB绘制洛伦兹模型的状态方程如下图：

MATLAB代码：
f=@(t,x)[-8/3*x(1)+x(2)*x(3);-10*x(2)+10*x(3);-x(1)*x(2)+28*x(2)-x(3)];
t_final=100;x0=[0;0;1e-10];[t,x]=ode45(f,[0,t_final],x0);
plot3(x(:,1),x(:,2),x(:,3));
%如果欲观察相空间轨迹走行最好的方法是采用comet3()函数绘制动画式的轨迹，即将最后一条语句改为comet3(x(:,1),x(:,2),x(:,3));

可以发现图像是混沌的，而且十分像一只张开双翅的蝴蝶。因此笔者以蝴蝶为素材，从代数，分析，几何以及概率中各挑选了一个公式作为代表融合起来设计。话不多说，直接上图：

Cauchy-Schwarz不等式

令x,y是两个向量，则

当且仅当x,y线性相关时，等式成立。

柯西不等式是由大数学家柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。但从历史的角度讲，该不等式应当称为Cauchy-Buniakowsky-Schwarz不等式，因为，正是后两位数学家彼此独立地在积分学中推而广之，才将这一不等式应用到近乎完善的地步。该不等式有多种形式。

Crofton定理：

令D是平面上有界凸区域。D的两条切线通过D外每点P(x,y)。令t_1与t_2是线段长，此线段由P与切点确定，令A是各线段间的角，被看作(x,y)的函数，则

Stolz定理：

令{x_n}与{y_n}是两个实数数列，{y_n}时严格正的，递增的，无界的。若

则极限

F=normcdf(x,μ,σ)

MATLAB语言，F为x各点处的正态分布的分布函数值

关注 哆嗒数学网 每天获得更多数学趣文

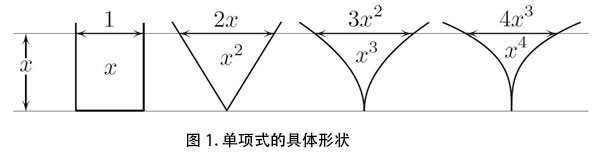
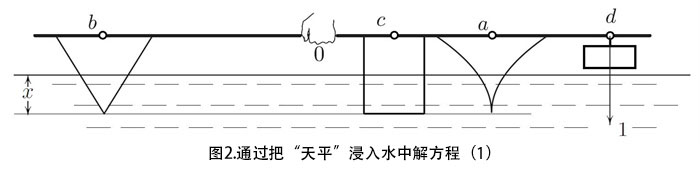
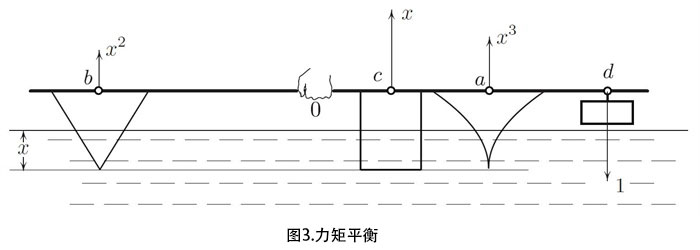
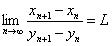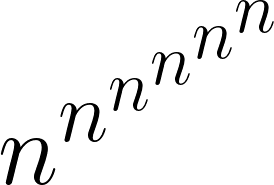原文作者，Marianne Freiberger，转自Plus网站。

翻译作者，小鹤e，哆嗒数学网翻译组成员。

校对：Radium

关注 哆嗒数学网 每天获得更多数学趣文

两位计算机科学家采用一种新方法把蛋糕分给任意数量的人，而不引起任何人的嫉妒，因而在切蛋糕理论上取得了突破。这个结果不仅仅与生日派对有关:无论是土地资源、播出时间还是石油资源，蛋糕可以代表任何连续的研究对象。从离婚诉讼到政治冲突，切蛋糕理论的灵感来自于各种各样的问题。

当只有两个人分蛋糕时，问题就很简单了。让第一个人切蛋糕，第二个人选择他想要的那块。第一个人会确保他切的蛋糕中的两个部分他都很满意。根据喜好和蛋糕上的东西，第一个人可能会把蛋糕切成两等份，或者切成一块小一块大，但小的那块有草莓。无论第二个人选择哪一块，第一个人都不会嫉妒。第二个人可能不喜欢切蛋糕的方式，但是，因为他或她先挑，所以也不会嫉妒第一个人的那块。一般来说，如果没有人嫉妒其他人的蛋糕，那么该分法就称为无嫉妒分法。

这种针对两个人的分法早已为人所知，但直到20世纪60年代，数学家约翰·塞尔弗里奇(John L. Selfridge)才发明了一种适用于三人最优而高效的方法(后来约翰·康韦(John H. Conway)也独立发现)。1995年，史蒂文·布拉姆斯(Steven J. Brams)和艾伦·泰勒(Alan D. Taylor)提出了一种突破性的方法，适用于任何人，但有一个缺点。即使只有四个人吃蛋糕，公平划分所需的切割步骤也可能是任意大的。为了找到划分方法主刀人需要问吃蛋糕的人一些问题——这与划分方法完成所需的时间有关——可能是任意大的。这个界限究竟有多大取决于参与者的偏好(如果你幸运的话，它们可能很小)，但关键是你不能从一开始就限制算法运行的时间和需要进行多少次划分。这尤其令人失望，因为数学家们确认，对于吃蛋糕的n个人来说，只需要切n-1刀就有一个无嫉妒分法。问题只是在于找到那个分法。

一种变动是允许移动刀：主刀人将刀(或几把刀)在蛋糕上移动，当吃蛋糕的人认为应该切蛋糕时大喊“停”。至少对于四个吃蛋糕的人来说，这使得切蛋糕的步骤减少到五步。但是吃蛋糕的人要做无数次决定。对于刀在轴上移动的每个点，他们需要决定是否喊停。由于我们真正想要的是一个可以在计算机上运行的离散分步算法，这种移动刀的方法并不完全令人满意。

由哈里斯·阿齐兹(Haris Aziz)和西蒙·麦肯齐(Simon MacKenzie)设计的这种新方法是离散的，它规定了切蛋糕的数量，以及主刀人需要向吃蛋糕的人提出的问题的数量。无界限方法的合作者Brams对这个结果很满意：“我相信Azizz - Mackenzie算法是一个重要的理论结果，肯定有所突破，而我们之前用泰勒得到的结果——通过限定算法所需的步长(或切割步骤)——证明了它是有限的，但我们无法确定它的上限。”

这就意味着像蛋糕一样的冲突可以在一瞬间解决了吗?不完全是——阿齐兹和麦肯齐的结果纯粹是理论上的兴趣。当涉及到n个吃蛋糕的人时，你需要问的问题的数量界限如下一个数：

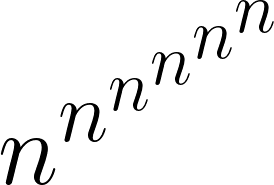
不管吃蛋糕的人喜欢什么，问题个数超过这个数字后，你都不需要继续问下去。但这仍然导致了难以想象的过大的界限:即使对于n=2，标准计算器也会崩溃。布拉姆斯说:“无论是否使用移动刀，要缩小这种界限都是一个挑战。”“然而，我不认为这样的数字会让这些算法有任何实用价值。”

还有一个问题。Aziz 和MacKenzie的方法保证了没有人会嫉妒别人的蛋糕。但这并不能保证每个人都满意。可能存在另一种蛋糕的划分，它让一个或多个吃蛋糕的人更满意，而且不会让任何人变得更嫉妒他人——用数学表达就是，无嫉妒法通常不是帕累托最优的。吃蛋糕的人可能会抱怨:他们可能不会嫉妒别人的蛋糕，但如果知道自己可以在其他划分方法中获得的更多，他们可能也会很不高兴。同时满足无嫉妒和帕累托最优往往是不可能的。因此，尽管理论家们在努力降低算法的界限，但现实中的实践者们需要认真思考，在特定的冲突中，哪种划分是最好的:无嫉妒、帕累托最优，还是其他一些标准。

如何把蛋糕分给三个人，使得三个人都不会嫉妒别人。

假设我们的三个人分别被称为A、B和C，我们不分性别地把每个人称为“他”。首先，C把蛋糕切成它认为有相同价值的三块。然后A和B各自挑选。如果他们选择两个不同的部分，这个过程就完成了。

假设A和B想要相同的一块蛋糕。在这种情况下，B会对它认为最有价值的蛋糕进行一些修剪，以匹配B认为第二有价值的那部分蛋糕。把切下来的余料放在一边，让A先挑。接下来，B选择他的那块，但有一个条件，如果A没有选择被修剪的那块，那么B必须选择它。最后，C选择。现在A不嫉妒了，因为它第一个选择。B不嫉妒，因为它的第一个选择是同等价值的:无论A选择什么，都有一个同等价值的部分留给B。C也不嫉妒，因为从C的角度来看，唯一降低了价值的部分，是被修减了的那块，但它会被A或B拿走，而最初的三个部分对它来说是同等价值的。

这样就剩下余料那部分了。假设在前一轮中被裁掉的蛋糕被A选中。让B把余料分成它认为有同样价值的三块。让A第一个选，C第二个选，B最后选。A不嫉妒，因为它先选。如果C嫉妒，那么它一定是嫉妒A，因为C在第一轮中是满意的，第二轮时，它选在B之前，所以它也不嫉妒B。那么C嫉妒A吗?在第一轮中，A选择了被修剪掉的那块蛋糕，也就是说，A在第一轮中选择了对C来说没有其他两块那么大的蛋糕。我们用V表示在C眼中最初3块蛋糕的价值。我们把W记为C眼中余料的价值。现在对C来说总价值是V加上W；而C眼中分配给A的价值是V-W加上部分W显然，V-W加上部分W的总是小于V，也就是说，C认为，A分配给A自己的价值小于C分配给它的价值，因此C不嫉妒A。

如果是B在第一轮中选择了被修剪的那块呢?在这种情况下，只需交换上一段中A和B的角色。

关注 哆嗒数学网 每天获得更多数学趣文

原文作者，Adhemar Bultheel。

翻译作者，风无名，哆嗒数学网翻译组成员。

校对：math001

关注 哆嗒数学网 每天获得更多数学趣文

牛津大学“极简入门”系列读物涉及了从会计学到“犹太复国主义”等等广泛大量的话题。这本《无穷》是其中最小的小册子之一(真正的袖珍书：174×111 mm).无穷这个概念，主要是在数学中具有重要性与实用性，不过它也拥有哲学的甚至宗教的一面。在这个“极简入门”所允许的情况下，斯图尔特(Stewart,本书作者)尽力做到内容广泛，在讨论中加入了大量的历史知识。对于仅有143页的小书来书，谈论的东西实在是太多了。虽然有大量的重叠之处，与马库斯·杜· 索托伊（Marcus Du Sautoy）的《如何对无穷进行计数》和尤金妮娅· 陈（Eugenia Chen）的《超越无穷》相比，斯图尔特的处理更加广泛。后二者更着重在数学专业性。

无穷即无穷大，曾经长久地作为一个模糊的东西，在哲学基础上进行讨论。古希腊人就实无穷与潜无穷的分别进行了争论。这个潜无穷即某个超越了所有的自然数的东西，通过“枚举”，它是永远不能被达到的。就“可公度性”（那时主要作为达到数学的几何途径）这个概念来说，它们与无穷小是不同的。无穷小超越了有限长度的任何可能小的分割。它们基本的公共的度量是有限的，这导致之诺提出了“之诺悖论”。十八世纪，牛顿与莱布尼兹引入了“无穷小量”克服了无穷小的这个难处。无穷小量表示了某种接近0但又不是0的东西。因为无穷小量不是0，在计算中，其它量可以除以无穷小量。不过，适宜得到结果的时候，无穷小量又被假定为0.那不是很严格的数学。直到十九世纪末，康托尔就无穷大的本质，给予了更深刻的洞见。通过这些历史，斯图尔特解释了无穷这个概念在多个领域怎样发挥了作用。这些领域对于我们今天如何理解无穷这个概念，都有巨大的贡献。

在第一章，斯图尔特提出了一些涉及到无穷的谜题或者悖论。这样，他阐释了仅仅说“无穷是什么超越所有数的东西”是不够的。无穷大需要更加严格的定义，无穷小也是如此。这些背后隐藏了无理数的过程就是例子：当台阶越来越细的时候，楼梯就越来越趋近正方形的对角线（译者注：这里的意思是用类似于楼梯的折线来近似正方形的对角线）；当边数越来越多的时候，正多边形就趋近于圆。这些以一个合适的方式展示了那个0×∞ 型求值的问题。希尔伯特旅馆，阐释了无穷大需要一个更加严格的定义。斯图尔特也给了其它的一些例子。为引起读者的思考，最先提出了这些谜题与悖论。就所有这些让人迷惑的叙述，斯图尔特的解释后面都会给出。

第二章解释了：在更高等的数学中，无穷并没有被隐藏起来，而是被嵌入到了基础微积分中。x>1的曲线1/x绕x轴旋转就得到了加百列号角这个图形。它有一个让人吃惊的特性：虽然表面积是无限的，不过其体积却是有限的。当然，无穷也隐藏在“0.9999...等于1”这里，这个事实让很多本科生感到震惊。就像在其它的很多章节一样，斯图尔特很注重历史：戴德金定义实数所用的分割本质上是无穷的对象；朗伯（Lambert）证明了π的无理性；在公元前600年的耆那教中，人们把很大的数语无穷区分开，等等。

第三章更加深入得探究无穷的历史。传统上，空间与时间是被假定为无穷的。不过，当考察无穷小的时候，情况就不一样了。人们在处理无穷小事物的时候拥有巨大的困难。之诺悖论这个例子解释了：无穷多个非0的数的和，可以是有限的。从古希腊开始，实无穷与潜无穷就被区分开了，这个讨论在哲学家之间延续了几百年。一些神学家甚至声称：上帝是“无穷”仅存的拟人化存在。

下一个章节讨论了无穷小，以及它如何触发了微积分的发展。无穷小量这个原初的历史概念，现在被极限这个概念代替了。1960年代当亚伯拉罕· 罗宾逊提出了非标准分析的时候，无穷小量这个概念又复活了。

在几何学中，无穷就是视野所在。它引导了文艺复兴中透视的发展。这在第六章有详细的讨论，解释了为什么一艘船接近地平线的时候越来越小，以及这如何导致了无穷远处的点与线的概念。欧式平面可以建模为“边界表示为无穷远”这样的圆盘。更具体地，无穷远的线让制作使用透视的绘画变得容易。最终这个讨论以这些想法而结束：射影几何，通过使用立体投影获得的平面与球面的双向映射，无穷远处的点在球面上与北极相对应。

无穷在数学中是一个有用的概念，不过，它如何出现在物理世界中呢？那是下一章所涉及的。在物理学中，无穷经常导致很糟糕的奇点。斯图尔特讨论了三个例子。彩虹现象的分析是一个光学例子。根据射线光学，如果光从某个特殊的角入射的话，彩虹的强度将会是无穷大。这个奇点使得光必须重新考虑为一种波。在牛顿的引力理论中，当两个质点间的距离变为0，它们的势为无穷大，这就出现了奇点。1988年，夏志宏通过解一个五体问题，引人注目的获得了含有奇点的非物理的解。黑洞是广义相对论中的奇点，在宇宙论中，大爆炸显然是一个奇点。斯图尔特在这里也解释了，当宇宙论学家以曲率为一个参数来确定我们的宇宙是否有限的时候，为什么他们是错误的。

最后一章讨论了这些问题：康托尔是如何得到“实数是不可数的”的证明的，这如何导致了集合论与超穷数，以及这如何引起了数学基础的的修正。数学家或者任何对这类数学背景文献有一点了解的人，都对这个故事很清楚了。不过，在这里，斯图尔特，再次追随了“谁做了什么，以及为什么导致最终的结果”这个历史演化过程。这里有大量的信息，由于展示得很紧凑，对于一般的读者来说，阅读过程并不总是轻松的。每一章都有一些参考文献，这对那些想要考查更多细节的读者也许是有益的。有一些精心阐述的方面，是远远超过解释无穷的（比如，彩虹的角度的计算，透视的几何学），不过这些话题，它们自己本身也是有趣的，并且它们在其它的处理无穷的地方是不会发现的。如果你仅感兴趣于无穷的严格的数学概念，上面提到的杜· 索托伊或者陈的处理也许是更纯粹的替代品。不过，在这个小册子中，即使是有经验的读者也有更多的场合学到一些新东西。虽然不重要，不过“那是我不知道的有趣的东西”这种一闪而过的体验，也将使得这本书值得阅读。

关注 哆嗒数学网 每天获得更多数学趣文