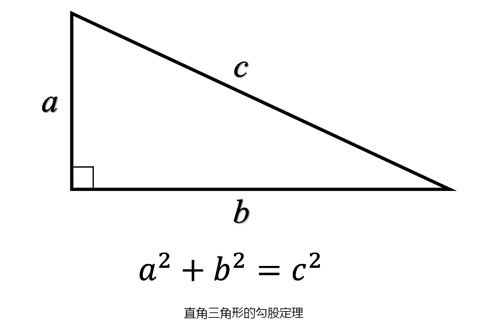
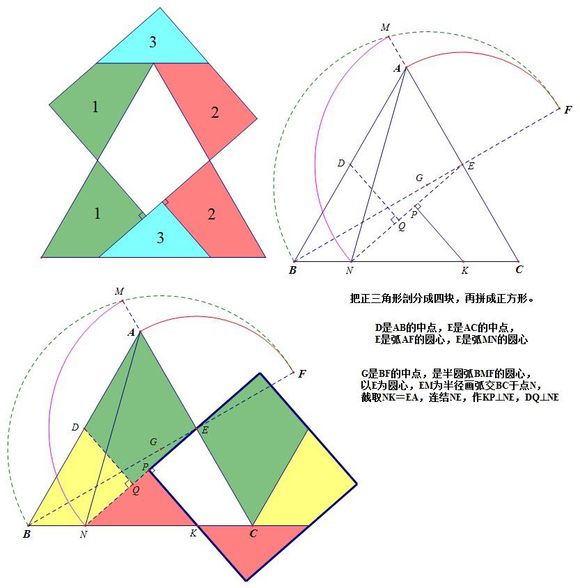
三位改变数学的女人
原文作者:AVERY CARR,原文载于科学美国人网站。
译文作者:e^iπ+1=0,哆嗒数学网翻译组成员,就读于上海科技大学
校对:333
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
——所有人都以为最伟大的数学家都是男人。不,你们都错了!
数学的历史,包括从对空间形状的深刻揭示,到可由想象与逻辑到达的最大程度的探索,似乎一直被男性数学家主导着。像高斯,欧拉,黎曼,庞家莱,埃尔德什,或者更近一些的数学家怀尔斯,陶哲轩,佩雷尔曼,张益唐,他们所有人都与最美丽的数学发现相关,并且全部为男性。
E.T. 贝尔于1937年所撰《数学精英》(Men of Mathematics)一书,就是一个例子说明这个“事实”是如何在公共意识中被加固强化的。即使在今天,男性数学家主导数学领域也不是什么秘密。但是这不能让我们忽视女性在数学上做出的革命性成就。有很多著名的女数学家值得我们感谢,感谢她们在诸如现代计算领域中,对揭示几何空间的问题上,对抽象代数的基石的构筑上,引导决策论的主要进步以及在数论和天体力学等领域中取得的成就,这使得人们在如密码学,计算机科学和物理等应用领域作出重要的突破。
像朱丽叶•罗宾逊在希尔伯特第十问题(数论问题)上的进展,埃米•诺特在抽象代数和物理领域获得的成果,以及阿达•洛夫莱斯在计算机科学领域里做出的天才成就,这三个著名的例子充分证明了女性数学家的贡献是非常重要的。
茱莉亚•罗宾逊(1919-1985)

在二十世纪之初,著名的德国数学家大卫•希尔伯特发表了二十三个吸引人,但却让绝大多数天才数学家也大伤脑筋的问题。其中第十问题描述为是否存在一般的算法可以判定所有的丢番图方程(整系数多项式方程)的可解性。设想,存在一个机器对于任意一个丢番图方程可以判别这个方程是否可解。数学家们常常通过简单而广泛的观察来处理大自然中无穷无尽又超乎解决能力范围的谜题。这个特殊的问题引起了伯克利数学家茱莉亚•罗宾逊的兴趣。经过了几十年的研究,罗宾逊与她的同事包括马丁•戴维斯与希拉里•普特南合作,最终给出了一种情况,否定回答了希尔伯特第十问题。
在1970年,一位年轻的俄罗斯数学家尤里•马季亚谢维奇利用罗宾逊,戴维斯和普特南提供的思路解决了该问题。由于其在数论方面杰出的贡献,罗宾逊成为了杰出的数学家,那是一个最重要的数学问题之一,罗宾逊为它的解决铺平了道路。在美国数学协会的一篇文章,“茱莉亚•罗宾逊自传”中,她的妹妹和传记作家康斯坦斯•里德写到“通常情况下,她永远不会刻意去收集自己的故事。但就她而言,她在数学上所做的一切工作都是重要的。”
艾米•诺特(1882-1935)
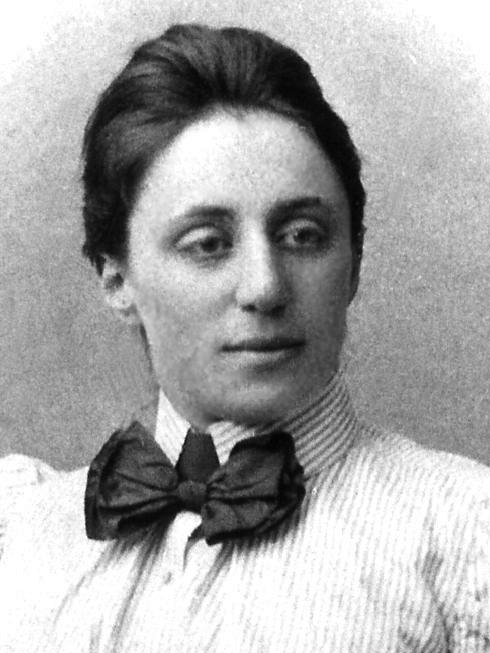
在抽象代数中浸润一段时间,会接触到一个经常出现的名字,那就是艾米•诺特。她的工作涉及的领域从物理到近世代数,使得诺特成为数学历史上最重要的人物之一。她1913年在变分法上的工作,诞生了诺特定理,被认为是最重要的数学定理之一,并且这个定理奠定了现代物理学的基础。 关于理想与交换环的诺特定理,形成了所有研究者对更高级的代数研究的基础。
她的工作的就像指引的灯塔,影响着那些想要更抽象地理解这个物质世界的人们。数学家与物理学家很欣赏她里程碑式的贡献,而这些贡献使得他们能够更深刻地理解各自的领域。在1935年,爱因斯坦写了一封信给《纽约时报》,“在所有现有数学家中,诺特是到目前为止,女性高等教育中培养的最伟大,最有创造力的数学天才。”
阿达•洛夫莱斯(1815-1852)

在1842年,剑桥数学教授查尔斯•巴贝奇在都灵大学做了一场关于他的解析机器(第一台计算机)的设想的讲座。此后,数学家路易吉•蒙博将讲座笔记转录为法语。年轻的女伯爵阿达•洛夫莱斯被查尔斯•惠斯通(巴贝奇的一位朋友)委托把蒙博的笔记翻译成英语。由于其在记录时富有远见的记法,她被公认为世界上第一位程序员。这份笔记在1843年被发表,洛夫莱斯在G部分增加了她个人的笔记,其中列出了一份计算伯努利数的算法。实际上,她利用了巴贝奇的理论机器,将它变成了可计算的现实。埃达•洛夫莱斯为那些想要探索计算奥秘的人提供了一条路,并持续地影响着科技的发展。
尽管她们的贡献意义深远,这三位女性数学家的发现却经常被男性数学家的贡献所遮蔽。据2015年联合国的估计,在世界上男人与女人的数量基本相同(101.8位男性对100位女性)。由此我们受到启发,工作在数学领域的女性应该和这一领域的男性有大致相同的数量。
我们之所以没能看到这一点,有个很重要的原因,是由于我们错误地认识了女性数学家的历史贡献。考虑到现代社会中科学技术的重要地位,我们认为促进和鼓励更多的女性进入数学领域,在一个文明社会里,是大势所趋的。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文