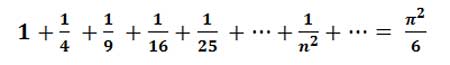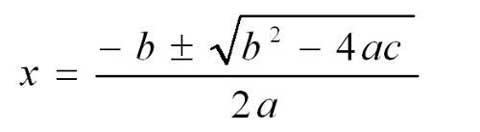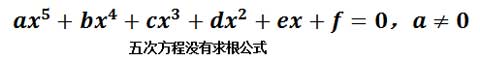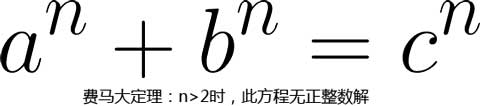作者,Sean Li 。
翻译,伯努利数,哆嗒数学网翻译组成员。
数学中有许多非常枯燥的事情。例如谁会关心(半径为r的)圆的面积是πr²,或者“负负得正”呢?为什么?也许我们可以在最出乎意料的结果上找到答案,反直觉的事实有时候甚至骗过了最好的数学家。
1、 生日悖论
生日悖论是说如果一个房间里有23个人,那么有两个人生日是同一天的概率将大于50%。这事实看起来很违反直觉,我们都知道在任何一个特定的日子里某人过生日的概率是1/365。

这种差异源于我们只要求两个人彼此拥有同一天生日即可。不然,若我们考虑的是在某人在某个特定的日子过生日,例如3月14日,那么23个人中,出现这种事的概率是6.12%。
换句话说,如果一个房间有23个人,而你又选择了某人X,并问他:“有人和你是同一天生日吗?”,答案很可能是否定的。但如果对其他22个人重复同样的行为,每问一次,你会更有机会得到肯定答复,最终我们会看到,这个概率将会超过50%(准确的说是50.7%)
2、 曼德勃罗集
德勃罗集是一个复数集,考虑函数f(z)=z²+c,c为复常数,在这为参数。若从z=0开始不断的利用f(z)进行迭代,则凡是使得迭代结果不会跑向无穷大的c组成的集合被称为曼德勃罗集。规则不复杂,但你可能没预料到会得到这么复杂的图像。

当你放大曼德勃罗集时,你会又发现无限个小的曼德勃罗集,其中每个又亦是如此...(这种性质是分形所特有的)

这真的很契合那句俗话“大中有大,小中有小”,下面有一个关于放大他的视频,我想这绝对令人兴奋不已。
如果你看了这些视频后仍然不觉得这些纯数学令人感到惊讶,那我也不知说什么好了。
3、 巴拿赫-塔尔斯基悖论
巴拿赫-塔尔斯基悖论是说,你可以将一个图形拆分后拼成两个各自和原先大小完全相同的图形。更特别的,它声称,对于一个3维实心球,可以将其分成有限份,而后拼成各自与原先的实心球大小完全相同的实心球。

很明显,这可是高度反直觉的。并且它被许多数学家视作数学中最为反常的一个结果。毕竟,在现实中,我们从未见过任何一个物体能凭空被复制成两个。事实上,它似乎挑战了物理中的质量守恒定律,即质量(在位移和旋转下)是不变的。但这个结果并非如此,似乎是在说一个物体的质量可以凭空变为原来的两倍?
不过,如果原来的质量是无限大的话。容易注意到无限大翻倍后还是无限大,那么从技术上看我们并没有打破物理法则。对于这个悖论更深层次的解释,可以搜搜其他相关的文章。
4、 蒙提霍尔问题
这个声名狼藉的问题表述如下:
假设你正参加一个游戏秀,给予了你拿走你选中的三扇门中的一扇门后的物品的自由。其中一扇后有轿车,另外两扇后各是一头羊,但你并不知道门后的物品。你选择一扇门后,记这扇门为1号门,而主持人知道门后的物品,打开了另外一扇门后有羊的门,记为3号门。然后主持人问道:“哪扇门后有羊呢?你想选择2号门吗?”。这时改变你的选择会对你更有利吗?
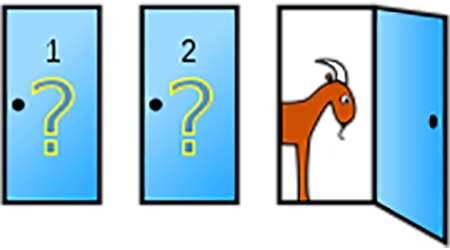
我问的人中,没有一个人能第一次就回答对。令人诧异的是,答案是最好换一扇门。
与其试着解释其中的缘由,我更希望推荐你们阅读维基百科的相关条目,阐述的非常到位,下面的故事也一样非常有趣:
“问问玛丽莲(Ask Mailyn)”的许多读者都不愿相信换门会导致更好的结果,而并不在意玛丽莲的解释。这个问题出现在Parade杂志后,有接近一万名读者,甚至包括接近一千名PhD写信给杂志,他们当中大部分都认为玛丽莲是错的。甚至在给予了解释、模拟、数学证明后,许多人依旧不能接受换门是最佳策略。甚至埃尔德什(Paul Erdos),史上最多产的数学家,直至在他看到电脑模拟证实以后,才能打消他的疑虑。
这一课告诉了我们,不要轻信自己的直觉。
5、 “加百列的号角”与油漆匠悖论
了解微积分的学生或许熟悉,“加百列的号角”是一个体积有限表面积无穷大的物体(用微积分的知识可以清晰地发现这一点)。

而它若在现实中,如果试着去漆上它,则会导致一些问题。油漆匠佯谬是说,我们可以填满这个号角(体积有限),但是却不可能完完全全的漆上它(表面积无限)。
“科赫雪花”是一种奇特的形状,与上例类似,它具有有限面积无限周长。事实上,第二个提到的曼德勃罗集也具有一样的性质!
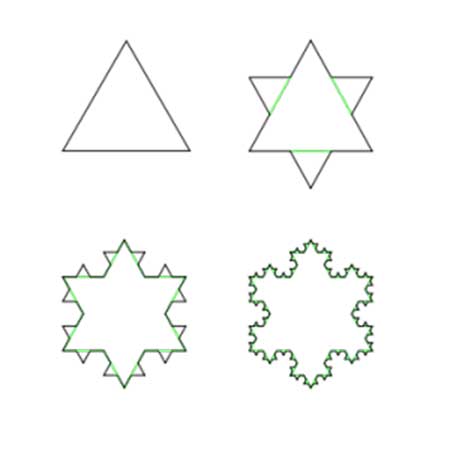
6.巴塞尔问题
巴塞尔问题说,如果你将自然数各自平方取倒数加在一起,那么你会得到π²/6。
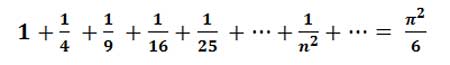
如果你是正常而且心智健全的人类,那么左边的这堆东西和π,这个圆的周长与直径的比值,会有如此联系这件事可能完全出乎了你的意料。
7、 阿贝尔不可解定理
你们大部分人在中学都接触过二次方程,也知道怎么解次数为2的多项式方程 ax² + bx + c = 0。
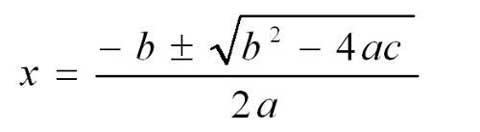
但我们的故事并不到此为止。在16世纪,数学家解出了一元三次方程,即ax³ + bx² + cx + d = 0。它对应的求根公式更为复杂:

感谢老天你并没有在中学学到这个,但让我们看得更远一点,怎么求解一元四次方程关于这一点,下面的求根公式可谓是骇人了:

我敢打赌你并没有看完它的整个细节。
现在让我们松口气,因为我并不继续要向你们展示后续的求根公式了,因为一元五次方程的求根公式并不存在!并不是说至今还没有找到,我们确确实实的证明了它并不存在。事实上任何高于五次次的一元多项式都没有求根公式。
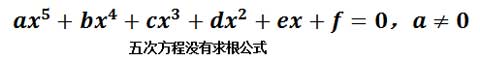
8、 有不同层次的无穷大
是的,有一些无穷大比其他的无穷更大。从学术角度而言,无穷大应该被称为基数,并且一个无穷大如果比另一个无穷大拥有更大的基数,则说它比另一个无穷大要大。(常规的自然数也是基数,但是无穷大的基数总是大于任何一个自然数的基数)
仍然有许多关于无穷大的基数的反直觉事实,例如,整数比奇数多吗?你可能理所当然的肯定,因为整数多出了一系列的偶数。但答案是否定的,因为他们拥有相同的基数。有理数多于整数吗?不,有理数与整数也一样多。
但是,康托发现实际上实数比有理数还要多。实数通常被认为是连续统,并且很长一段时间中,有过猜想,但至今并不能清晰的知道,是否有介于整数基数和连续统基数的无穷大?这个猜想被称为连续统猜想。
随后被发现,连续统猜想在通常意义下既非真也非假。它被证明并不能被证明或被证明为假(多读几遍,有点饶舌)。准确的说,保罗柯恩证明了连续统假设是独立于ZFC公理体系的,这是数学集合论中的标准公理体系。
9、 哥德尔不完备定理
简单的说,我们证明了有一些东西是不能被证明的。这个结果有大量初等的严格表述,我简单叙述如下:
(1) 任何一个足够强的系统存在一个命题既不能被证明也不能被证伪(例如连续统假设)
(2) 任何一个足够强的系统都不能证明它自身是不推出矛盾,即便它不能被推出矛盾

以上两条定义即著名的哥德尔不完备定理。显然,这些结果蕴含了巨大的意义,并不仅仅是数学上的,也有哲学上的。
10、 费马大定理
毕达哥拉斯定理声称,对于任何一个直角三角形,都有a²+b²=c²。现在假定这些变量都是正整数。那么显然有解a=3,b=4,c=5,但是a=1.5,b=2,c=2.5就不对了,即便它也使得等式成立。可以发现,显然有无穷多对使得a,b,c都是整数的解。
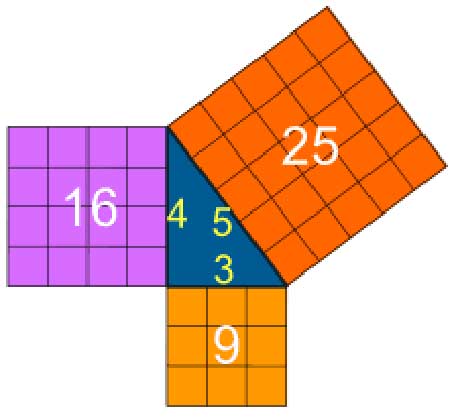
但如果我们进一步考虑下面的问题呢,有多少对正整数解满足 a³+b³=c³?答案是没有。就算再把指数3换成5也如出一辙,也无解。
事实上,费马大定理称,任何指数大于2的上述等式,没有任何一组正整数。这个著名的问题在1637年作为猜想提出,花费了将近四个世纪才被解决,最终被安德鲁怀尔斯于1995年解决。
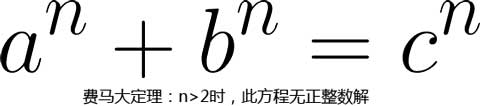
关注微信:DuoDaaMath 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa