原文作者：Meena Boppana，撰写此文时是哈佛大学大三学生。

译文作者：白公分，哆嗒数学网翻译组成员，就读于中国农业大学。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

这是Meena Boppana的发的来宾博文，Meena Boppana是哈佛大学的大三学生，而且是哈佛本科生数学协会(HUMA)的前主席。Meena热衷于传达在数学上的性别差异，并且与其他人共同参与发起了哈佛数学调查项目和数学男女容和组织(Gender Inclusivity in Math , GIIM)。

2012年，我怀着对数学的热爱踏进了哈佛的大门。4岁时，我就在我的男女平等主义者的数学家父亲的鼓励下开始思考数学，我甚至在高中做了一次TEDx演讲来表明我对这门学科的热爱。我确信我的能力和兴趣足以使我去学数学专业。

这就是为什么，三年后，我要思考这样一个事，几乎我所有有着深厚数学背景（比如数学竞赛的明星）的女性朋友都决定不学数学专业（我选择了计算机科学）。这一年，最有激情的新入学的数学55a班没有女生，只有两名主修数学的女生毕业。另外，哈佛数学系几乎没有一个女性终身教职。

所以，我决定做一些统计分析，并且与其他人共同指导一个关于哈佛本科生数学的调查。Nancy Hopkins和MIT的其他女性科学家先驱们的工作鼓舞了我，她们量化了学术机构里的性别不公—甚至是办公室的面积，这确实引发了一些改变。在所有主要学习数学（包括相关的理工学科）的哈佛学生中，我们得到了1/3的回复率，总计150人做完了调查。

我们调查分析的主要发现是哈佛数学系女性的稀少远不是由高中到大学的衔接问题造成的。所以，来到哈佛的女生的数学知识较少所以不修数学专业的说法很片面。在哈佛学习的几年里，女生的数学是不断掉队的，无论是论文还是深造率，都远低于同样条件的男生。

这是文化问题。我们的调查显示，很多女性愿意加入哈佛数学系，但是不能如愿，性别差异导致很多女性觉得不舒服，很多女性在数学系的公共场所感到不舒服。

讨论性别差异这一简单的行为已经引发了一个大讨论。我以前一直认为没人关心性别差异，因为没有人谈论性别差异。但是这次对哈佛数学系150人的大致男女均等、师生均等的调查过后，我意识到我的同学们无论男女都更多的感到无能为力而不是无动于衷。

这种情况很糟糕，但也不是无药可救。与一个大一男生一起，我发现了一个叫做数学男女容和组织(Gender Inclusivity in Math , GIIM)的哈佛学生团体。这个俱乐部有增加数学女性社区，包括宴会、进修、女性系列演讲，和传达数学系的性别差异、跟踪调查趋势和数学上的性别差异的讨论的的双重目标。

团结男性支持者是我们俱乐部的核心任务，我们收到的来自男性学生和教职工的支持力度让我们对改变保持乐观。

归根结底，是我对数学的热爱使我做出这些行动。数学太过美丽和重要（或者说更多的是考虑到人种和基础知识的不公平）以至于失去了50%潜在的爱好者。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者：Chris K. Caldwell，田纳西大学马丁分校教授。

译文作者：豆浆，哆嗒数学网翻译组成员，互联网行业数据分析师。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

素数的最新记录：2^74207281 – 1(x^y 表示x的y次方)，它有22338618位数，由Cooper, Woltman, Kurowski, Blosser 和GIMPS 在2016年1月7日发现的。

1. g(n)的介绍以及定义

一个很常见的问题：连续素数的间隔可以有多大？在我们回答这个问题之前，让我们先来谨慎地明确间隔的定义（有两个不同的常见定义）。对于每一个素数p，使g(p)等于p和大于p第一个素数之间的合数数量。因此，设第n个素数为p_{n} (p_{n}表示字母p的下标是n)，我们有：

p_{n+1} = p_{n} + g(p_{n}) + 1

.

即,g(p_{n})是p_{n}和p_{n+1}之间的间隔的大小。

由素数定理我们知道小于n的素数大约有n/ln(n)个，所以ln(n)是小于n的素数之间的平均间隔。然而，这些间隔会有怎样的宽度范围呢？下面我们将会讨论这个问题的几个方面。

2. lim inf g(n) = 1(?) 和 lim sup g(n) = 2

首先要注意的是孪生素数就是使得g(p) = 1的p, p+2，所以从孪生素数猜想我们就有这个猜想：有无穷多个p，使得g(p) = 1（或者等价于lim inf g(n) = 1）。

第二个需要注意的是g(p)可以任意大。不妨令n为大于1的任意整数，考虑下面这个连续的整数列：

n!+2, n!+3, n!+4, n!+5, ..., n!+n

注意到2可以整除第一个数，3可以整除第二个数，以此类推，n可以整除第n-1个数，证明了这个数列的所有数都是合数。所以如果p是小于n!+2的最大素数，那我们就得到g(p) > n-1。显然，应该还有产生相同间隔的更小的数。例如，素数42842283925351与它后一个素数之间有777个合数。——这是间隔为777的最小的素数，并且它远小于778！+2（一个有1914位数的数）。（也可以使用更小的数，不大于n的连续素数乘积：n#，而不是使用n!）.

最后一段，我们已经证明 lim sup g(n) = ∞，然而因为平均间隔是关于ln(n)，所以我们期望得更多。Westzynthius在1931年证明了：lim sup g(n)/ln(p_{n}) = ∞ 。

意味着对于每一个B>0，都有无穷多个素数p满足g(p) > B log p。在我们讲述更多之前，我们应该来看看数据上的证据。

3. 记录素数间隔的表格及图形

在下列表格里，我们列出了最大间隔在381以内的情况。这些是首先出现的至少是这个长度的间隔。例如，在素数277900416100927之后有一个879个合数的间隔（才出现下一个素数）。这是首先出现的这个长度的间隔，但还不是一个最大的间隔，因为素数218209405436543之后紧接着有905个合数。

首次出现的间隔

对每一个非负整数g，令p(g)是最小的由至少g个合数跟着的素数。这个表告诉我们p(148) = p(149) = ... = p(153) = 4652353。

根据上述值，我们在下边画出lnp(g)与g的图像。可能你开始明白为什么Shanks在1964会猜想：ln p(g)  ~  sqrt(g) (sqrt表示开根号)

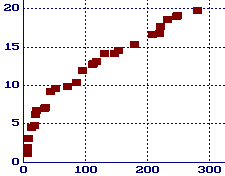
而且Weintraub在1991年估计：ln p(g)  ~  sqrt(1.165746g)。

4. g(p)的界

给定p，可能g(p)就会有一个上限。通过素数定理我们就能证明，对于任意实数e>0，存在某个整数n，使得总存在一个素数p满足：m < p < (1+e)m(对任意m > n)

这证明了，对于所有的p > max( n,1+1/e )，有g(p) < ep。或者更简洁地说，对于n > k，有g(p_{n}) < ep_{n}。)这里有几个关于e,k的具体数对：

对于n > 9, 有 g(p_{n}) < (1/5) p_{n} (Nagura 1952)

对于n >118, 有 g(p_{n}) < (1/13) p_{n} (Rohrbach & Weis 1964 )

对于n >2010760, 有 g(p_{n}) < (1/16597) p_{n} (Schoenfeld 1976 )

1937年，Ingham在Hoheisel的开创性工作的基础上加工，从而证明了：p^(5/8 + eps)的某个常数倍是g(p)的上界（对于任意eps > 0）。许多人已经对5/8进行改进，我所知道的最新的记录是0.535，由R. Baker 和 G. Harman完成（但肯定的是，在现在这已经被改进了）。

.

5. g(p)/ln p , g(p)/(ln p)²又如何呢？

再次，素数定理证明g(p)/ln p的均值是1，但我们怎么认识g(p)/ln p这个数列呢？Ricci证明这个集合的极限点集具有正的勒贝格测度，但迄今为止被证明的极限点只有无穷（上述提到的点）。

对于lim inf g(p)/ln(p)的各种上界已经被发现，包括0.248（当然，孪生素数猜想和素数K元组猜想都要求下限为0）。在一个相关的猜想，Cramer猜想：

lim sup g(p)/(ln p)² = 1

Granbille修改了Cramer猜想，揭示了它低估了间间隔的大小，Granbille猜测，对于任意一个小于欧拉常数的常数c：有无穷多个p，使得g(p) ≥ 2e^{-c}ln²p。这里的常数c类似于Merten定理的常数M。

这个猜想可以被证明吗？还不行，但是Cramer表示，如果黎曼猜想被证实了，那么我们就可以得到一个比较弱的结果：

g(p)<k ln p sqrt(p)。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

根据中新社2016年4月16日消息,中共中央政治局常委、国务院总理李克强15日到清华大学和北京大学就教育改革发展和实施创新驱动发展战略进行考察。

李克强总理是上午考察的是清华大学，而下午来到北京大学继续进行考察。其间，李克强总理造访了北京大学的数学科学学院。

数学科学学院建国以来共培养出30余名两院院士。李克强来到这里，详细了解基础数学研究进展和后续人才情况，听到这几年报考数学专业的学生明显增加，李克强欣慰地说，数学是自然科学皇冠上的明珠。中国与世界发达国家在科学技术上存在差距，很大程度上是基础研究特别是基础数学存在“短板”。希望把基础数学研究放在重要位置，有一批人能够静下心来甘于坐“冷板凳”，把板凳坐热。要建立对基础研究长效支持机制，让教学和科研人员拥有合理稳定的收入保障和受人尊敬的社会地位。

李总理在公开场合下对基础数学表示关心与支持已经不是第一次了，2015年1月27日，国务院总理李克强在北京中南海主持召开座谈会，复旦大学校长许宁生就被问道：“复旦大学这几年报考纯数学的人数是多了还是少了?”其间也是提到了很多高新科技领域中国之所以落后是因为数学的落后，代表世界数学最高水平的菲尔兹奖中国至今也没能获得。

当时，这条消息已经足以让哆嗒数学网的粉丝讨论一段时间了——总理居然知道菲尔兹奖这个奖项，真是让人感到意外的事情。李总理又一次公开的力挺数学，而且还是基础数学，各位高端的数学粉丝们，加油吧，咱家强哥看好你哦！

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

这是芝加哥大学数学系Hirschfeldt一篇文章的引言部分，原文的全文地址是http://math.uchicago.edu/~drh/Papers/Papers/rm.pdf。该文全文是非常专业学术文章，但这篇这篇文章的引言写的非常有趣，实际上可以作为可计算理论和反推数学的一个科普级别的介绍。

原文作者：Hirschfeldt，芝加哥大学数学系。

译文作者：Math001，哆嗒数学网网主。

文章校对：小米，就读于纽约大学柯朗数学研究所。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

每个数学家都知道如果 2 + 2 = 5 ， 那么罗素就是教皇。据说罗素曾经在一个讲座上用下面的方式证明上述结论：如果2 + 2 = 5，那么，在等式两边同时减去3，得到 1 = 2。 因为教皇和罗素是两个人，于是他们是同一个人。当然，按经典逻辑学的观点，我们根本不需要这样的一个证明，因为一个永假式的前提可以推出任何一个命题。 从逆否命题的角度看，如果结论永远都是真命题，那么任何前提假设都能推导出它。但是，假如我们真的认真地对待一个需要证明的命题，比如说，如果四色定理成立那么质数就有无限多个，那么你们之中谁又能回答如下问题：证明上述命题的时候，在哪些地方会“真正用到”四色定理？这类问题看起来又难又没意义，但是数学老师总会把类似的基础练习布置给你。“用波尔查诺-维尔斯特拉斯定理证明[0,1]闭区间上的连续实函数是一致连续的。”就是这样一道数学分析中的经典习题。另一个类似的问题是“哥德尔第一不完备定理的蔡廷信息理论版本是否能证明出哥德尔第二不完备定理”，这则是Kritchman和Raz最近一篇有趣的论文。

还有一类常见的问题，要求你不能使用一些特定的数学方法来证明一些数学命题，比如，不使用算数基本定理证明根号2是无理数，或者，用初等方法证明质数定理。我们也听到数学老师以及同学会谈及类似这样的事情：“定理A和定理B是等价的。”、“定理D并不能直接推导出定理C”或者“用引理E证明定理F非常方便，但定理E并不是必要的。”。这些东西往往能成为理解某个数学领域的关键。

还有一些东西能帮助我们把不同领域的数学联系起来。比如我们来思考一下下面的一系列定理：[0,1]闭区间上的连续函数上确界存在定理、常微分方程局部解的存在定理、哥德尔完备定理、可数交换环的素理想存在定理、布劳威尔不动点定理。这些不同的定理证明过程可能是相似的，本质核心都是围绕紧性在讨论问题，同时，也可以把他们看成基本组合思想在不同数学分支中的反映，都用一个叫做弱柯尼希引理的东西来解释——这个我们在后面的部分会详细讨论。我们会在4.4章节把这个问题严格化。

本文里，我们将讨论两种紧密联系的数学方法:可计算数学与反推数学。通过它们我们可以在各个可证明的命题之间，给出关于“蕴含”和“不蕴含”概念的严格精确的数学意义。 我们会将目光集中在一些组合原理上，它们易于陈述和理解，但从这些观点来看却展示出错综复杂而又美丽迷人的一面。这篇文章并非关于这个领域的一些研究成果的综述，而是一系列该领域思想和方法的介绍。文章更多的会依照我自己的兴趣（尤其是可计算理论和反推数学的组合分析以及拉姆齐二染色定理相关的模型论原理）来写，但是我还是希望尽可能的吸引和刺激一些新人进入这个领域；特别地，虽然反推数学的逆推过程和数学基础密切联系，但我并不想对这个方面的事情说太多。

虽然我会在2.1章节简要回顾一些可计算理论的基本结论，但我还是假设读者已经知道一些数理逻辑的背景，尤其是可计算理论的基础知识。否则，这篇文章需要写的东西会包含得太多。文章中间会散布一些习题，解答这些习题也是阅读这篇文章不可或缺的工作。文章中还会提到一些没有解决的公开问题，我们鼓励读者去挑战他们。没人知道一个睿智的思想什么时候会闪现并攻克一个长期没有解决的问题。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

作者， SAMUEL ARBESMAN ，此文原载于WIRED网站。

翻译，donkeycn，哆嗒数学网翻译组成员，华东师范大学数学博士。

众所周知地，我们的直觉并不总是完美的。在日常生活中相当多的方面，可以预见的是我们理性的力量是不够强大的。当我们遇到稍微深奥一点的事情时，我们又能做什么呢？我们使用我们的理性——我们的能力来做推断和预测，最终却依然可能会失败，原因很简单：因为事情往往太复杂了。这种情况似乎体现在我最近在 Quora（译者注：一个问答SNS网站）上碰到的一个问题：有哪些猜想是因为一些“非常大的数字”的反例，从而导致它被证明是错误的？

从本质上讲，提问者感兴趣的是如下情况：有哪些数学猜想刚被提出来时看上去是对的，但是推翻它反例却远远超出人类本身的计算能力，只能用先进的应用程序来证明它是错误的。

这样的情况有很多。一个比较著名的例子是波利亚猜想。这个猜想说的是：给定一个正整数N（译者注：N≥2），所有不超过N的正整数中，有偶数个素因子（译者注：素因子数按重数计算，1的素因子数定义为0，）的数不超过有奇数个素因子的数。直到当你检验906150257这个数之前，这看起来都是对的。但是我们的感觉错了。

另一个例子来自欧拉猜想：

十七世纪瑞士数学家莱昂哈德-欧拉声称如下方程就像费马大定理中的方程一样没有正整数解：

二百年来，没有人能证明欧拉猜想，但另一方面，也没有人能找出一个反例来否定它。首先是人工搜索，然后是多年的计算机筛选都未能找到一个解。没有找到反例是这个猜想成立的强有力的证据。然而在1988年，哈佛大学的 Noam Elkies 发现以下这个解：

尽管二百年来都没有找到反例，但最终欧拉猜想被证明是错的。事实上，Noam Elkies 证明了这个方程有无穷多个解。

正如 Singh 所注的（译者注：此处指 Simon Singh 及其所著的《费马大定理：一个困惑了世间智者358年的谜》）：“这里的教训是，你不能通过只对前一百万个数字来证明一个猜想对所有的数都成立。”

这些实例是迷人的。他们表明，再大的数字也不是无穷大，故而并不能成为证明。我们人类的大脑是强大的，但我们必须更多地与机器的合作，以帮助我们突破我们直觉的束缚。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者：Eddie Krassenstein 

译文作者：小饕，哆嗒数学网群友。

毋庸置疑，学生时代的我实在对数学不感兴趣。我实在是不想看到那些各种绕来绕去的数字。尽管各个年级的数学课我从来没有不及格过，但我还是得承认，毕业的那一刻起我就从来不会想念数学这个学科。话又说回来，并不是所有人都有同样的感受。数学对于其他人来讲可以是那样迷人，尤其是关系到几何形状中分形的时候。

总的来说，分形就是由有着相同统计特性的部分组成的曲线或几何形状。它们存在于人造的构型和物体中，同时也神秘地存在于大自然中。对于Jérémie Brunet来说，分形一直都是那样令人陶醉。

“八十年代当我十几岁的时候，分形就深深地吸引了我。”Brunet告诉3DPrint.com，“父亲很久以前给了我一本名为《分形之美》的书，我至今还珍藏着它。我曾经在旧电脑上编程构建分形，也徒手画过。大概是五年前吧，onfractalforums.com网站上的一个协作项目中出现了新一代的3D分形，于是我又无法自拔。”

那天，Brunet偶然发现了 Shapeways 。很快，他不得不“赋予这些古灵精怪的数学对象以实体”的事实就显而易见了。

“我希望能打破分形艺术的局限性，而3D打印技术就是能够达到这个目标的一项完美的科技，”Brunet解释道，“对我来说，它们很好地诠释了自然之美妙，宇宙中精细的准则以及简单规则和基本元素之下衍生出的复杂性。如今，受限于分形界定中过多的细节要求，制造3D打印分形仍旧面临了许多困难。但我依然热衷于坚持不懈地打破和延伸3D分形的界定范围。”

目前，Brunet大约有一百多个价格不同的分形在Shapeways shop出售，有的不到10美元，还有的要几百美元。从大件的塑料打印产品到金银铜制成的小件珠宝，应有尽有。Brunet对Shapeways十分信任，没有选择基于FFF的台式打印机上打印它的设计，仅仅是因为这些机器不能给予他所需要的复杂细节。

“我希望能够尽可能地尝试并自由搭配各种颜色和材料，”Brunet告诉我们，“我坚信有一天，可以买到既便宜又有很高分辨率的金属台式3D打印机，到那个时候我很可能会投资。”

对于单个分形的设计，他们需要大量的辛勤工作和时间。工作流程十分复杂，包括从Mandelbulb3D（一个免费的分形生成软件）的立体像素堆输出。在一个叫做“行进方块”算法的过程中，这些东西组成了一个三角网状结构，之后在Meshlab中进行后期加工和完善。最近Brunet开始使用另外一个名叫 Incendia EX的软件包，这个软件提供了一个特殊的功能：直接输出STL文件。

Brunet还告诉我们，在Shapeways上销售了不少分形的同时，他花了比挣来的还要多的钱去购买分形。他希望在今年或明年能够打破这个局面，即使一天也罢。无论如何，3D打印分形为他带来了不少关注。

 “最近，我做的雕塑之一在 德克萨斯西南大学的Brown Symposium 上展出。它作为一个名为《What Things May Come》的3D打印艺术展的一部分。即使这只是一个爱好，我的下一个大规模的计划是参与一个重量级的3D打印分形寺院的建造，为的是内华达州的燃烧人节，最好是在2017年。敬请期待！”

即使我不像Brunet那样对数学感兴趣，我的确十分欣赏这些由他创造出的设计。我可能最后会给自己买几个他做的不可思议的分形。你觉得Brunet的分形怎么样呢？你自己购买过它们吗？在3DPB.com网站中的3D Printed Fractals forum讨论讨论吧。还有，一定要看看Brunet的YouTube channel和以下的精彩图片。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者：Dan Rockmore

译文作者：e^iπ+1=0，哆嗒数学网群友,就读于上海科技大学。

我参观了两个在曼哈顿西区展出的展览，展览将数学和视觉艺术很好的结合起来。一个是在惠特尼美术馆展出的弗兰克•斯特拉回顾展，另一个是在南希霍夫曼画廊展出的一个画展。如果你喜欢艺术与数学的结合（正是艺术教我们如何从“STEM（科学、技术、工程、数学）教育”转变为“STEAM（科学、技术、工程、艺术、数学）教育”！），而且若你有些精力漫步于数学艺术中，那我推荐你可以去纽约现代艺术博物馆游览。

在我看来，纽约现代艺术博物馆经常将与数学相关联的展品放在一起，其中有一些很显然，但有些则不容易看出。这一次的展览中，两种类型的展品都有所展示。对于前者来说，可以看一看无尽之屋(Endless House)这个优美的小型展览，其中展示了很多建筑模型，其中一些房屋的设计灵感来源于甚至取名于一些基本的数学对象，如环面（如普林斯顿•斯科特•科恩的《环面屋》(Torus House)）和莫比乌斯带（鲍斯/范•伯克的莫比乌斯的房子）

事实上，几何学的灵感和美感（除了明显的在工程上与数学的联系）对建筑的影响有很长的一段历史，早在古希腊时期，就已经将经典的几何形状如正方形和圆形应用到他们的结构中去了。无尽之屋这样的展品明显表明这样的影响还在延续。

谈及展览的名字，无论环面还是莫比乌斯带，其实都是有限实体也可以创造无限的例子。圆环可以说是数学家的结婚戒指，而且被许多人认为是无尽之爱的最好的典范。而莫比乌斯带从另一方面来说，是一枚扭曲的婚礼戒指。更精确地说，取一条纸带，先拉直，再半扭曲，最后将两个相反的终端相接，并且从连接的一端开始使之成为一圈。如果你是一只蚂蚁，那当你回到连接点的边界，将会完全颠倒过来。继续走直到你再一次回到出发点，你又会颠倒，重新回原来的状态——也许这是一个关于婚姻的隐喻。假如你是一只沿着中线爬行的蚂蚁,最终会发现你处于颠倒的状态。无论方向是保持不变还是反转，在有限的空间里都会给出无限的感觉，而这无疑是建筑上和数学上的期望。

几何主题也在其他两个正在展出的优美展览中延续——但是这些作品中数学并不是很显而易见，虽然在很多情况下这更加迷人：在纽约现代艺术博物馆的二楼你可以发现一个简洁但富有思想的展品，这是来自于杰克逊•波洛克的作品，以及在角落里一个一鸣惊人的雕塑作品，来自于巴勃罗•毕加索。现在我将试着阐述当我行走于这些展品间，通过数学的眼光我看到了些什么。

波洛克因其“滴色绘画”而被众人知晓，它是通过将颜料抛洒到放在工作室地面上的画布上完成的。波洛克会在画布上舞动，同时巧妙地指挥刷子上的油料，犹如芭蕾舞舞蹈一般，所以他被认为是最初的“滴色派画家”。他认为作品最好的状态是自身意图和意外惊喜的奇妙杂糅（即使在移动中，他仍旧对画作有艺术名家般的控制），画布上记录着他的行动和创想。

在波洛克很多的作品中都可以看出“随机”——这是一些无法辨识的图形——但事实上，在数学小小的帮助下，波洛克作品中的很多随机程度都是可以被量化的。在1995年，物理学家理查德泰勒发现可以用数学上的分形集合来研究波洛克的工作。一幅“分形的图像”可以被描摹为它可以惊奇地出现在自身每一个比例的图像中，当我们越来越细致的观察它，它永远不会被完全“填满”，而不能被填充的原因是其所具有的某些规律性质。也就是说，如果你使用一台显微镜去观察分形图像，即使你提高它的放大能力，也不可能看到一个点，而是看到难以名状的一团图像。当然，在图像上会有很多的洞。此外，无论你怎么看，从物镜看到的区域总是和总体保持一致性。你可以计算这个图像的维度。鉴于直线是一维图形，被填满的区域是二维图形，波洛克作品的维度看上去像是介于这两者之间。这就是说处于分形维度。数学家曼德布罗特发明了“分形”这一概念去描绘这些结构，并且在各种不同的自然（甚至经济）现象——从海岸线到山脉，从树叶到花椰菜茎。当被问及他的工作过程时，波洛克因其他说“我是自然的”而著名。从数学的角度上来说他是非常正确的。

有趣的是，泰勒是从他的艺术作品中获得了这个灵感：那还是他学习艺术时在一年的休假中所做的最终作品的一部分。泰勒建构了精巧的装置使得利用风来完成他的画作。他注意到自己所创作的画作和波洛克的滴水画作有一定的相似度，此外，他知道风的运动（湍流）可以产生分形现象（想想从烟囱里飘出的炊烟被风吹成涡流的形状）。泰勒的作品想来饱受争议——特别是将他的画用作认证波洛克的画（他曾经有一段时期是波洛克-克拉斯纳基金会的顾问）—— 但分形的计算和其数学联系非常吸引人去探索。

现在在纽约现代美术博物馆的大作应当是毕加索雕塑展览。众所周知，毕加索通常被认为是“立体主义”的创始人，这是一项二十世纪初发起的艺术运动，倾向于用直觉解构物体的表现，它通常是在单幅作品中堆叠融合各种视图。通过这种方式将三维模型直观地转为多个二维视图的重构。在上一次的展览中我们认识到毕加索“可以灵活运用多角度的观点”。立体主义因此成为一个立体视觉的艺术探索，它通过将左右视网膜上独立的二维图像进行整合从而来产生三维体验。《女人头像》（巴黎，1909），毕加索早期最有名的雕塑，被认为是他的立体主义大作，体现了二维堆叠的想法。从为这次展览所写标签文字中可以知道，破裂面和翻光面构成了雕塑的表面，这也标志着这是一个媒介上对立体主义的一种探索。

通常来说，立体主义的历史呈现为塞尚平面画作的自然进化。但这里又有另一个有趣的故事，有人注意到数学和物理学上同时期的发展，发生在相对论这一跨世纪的发现，其中大量使用了四维思想，为理解世界打开走出了一条新的路。在《爱因斯坦、毕加索：宇宙、时间、和动人心魄之美》一书中，科学史家亚瑟•米勒认为在毕加索的智慧结晶中相对论的发现还有很多值得深究之处，这是围绕思考四维的神秘与复杂的普遍思潮的一部分。

米勒在Espirit Jouffret的关于四维几何的通俗读物（《初论四维几何》1903年）与艺术建立了有趣的联系（通过莫里斯•潘塞，是一个保险推销员，也是毕加索认识的熟人）。在书中他通过多重的二维投影和三维投影来阐释四维物体，而不是用一堆平面视图来表现三维实体。Jouffret的直观解释，比如以下这张图，用以解释超立方体，从我的角度来看，这暗示了很多早期立体派作品Jouffret不是唯一一位为大众创作关于四维的书。在英吉利海峡的另一端，艾特温•阿博特，其著名的数学书籍《二维国》用不同的方式拟人化了四维。《二维国》部分是数学普及读物，部分是社会评论与讽刺作品（包括对几何元素卡通般的拟人化，从高傲的多边形到谦卑的点）。它阐释的方法是通过类比在二维平面生活的人类的视觉体验，将三维的读者投放到四维空间中。这些二维国的生物生活得犹如悬浮在最细的纸张里。就其本身而言，他们没有办法感知上下或者离开纸张，而我们也仅仅只是能想象离开我们所存在的空间。二维国里的生物可以被认作是封闭的，被嵌在纸张里。然而，作为二维国外的观察者——当我们观察纸张时——事实上我们能看到这些生物的内部！类似的，一个存在在四维空间的人同样也可以“识透”三维实体。

从这个角度上，让我们现在再回到毕加索展。在展览的二号房间我们发现了毕加索另一幅最为著名的作品，《吉他》（1914）这—不是对乐器的简单复制，更确切的说是同时展示吉他的内部和外部。也暗示假如这吉他存在于四维时空，或许有人会拥有这种吉他。

几何学这门学科，脱胎于人类想要理解周遭世界的渴望。我偏向于认为艺术至少有一部分是出于同样的动机。这个月在纽约艺术博物馆，可以来看看数学和艺术是如何以令人惊讶的和美丽的方式走到一起。若你真的有机会来这里欣赏艺术，且持有一份开放的心态，当你行走其中，比如沿着莫比乌斯带旅行，离开时你会发现自己正在思考数学。

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa