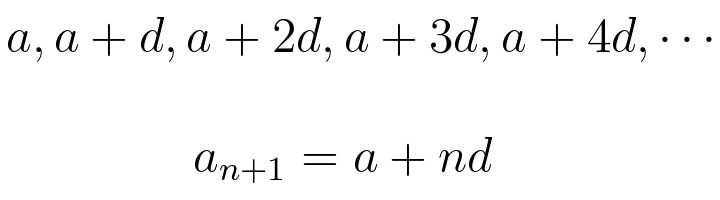二胎政策中的数学
原文作者:Jorge Almeida,任教于葡萄牙的里斯本大学,教授遗传学。
译文作者:donkeycn,哆嗒数学网翻译组成员,华东师范大学数学博士。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
中国刚刚取消了独生子女政策。如何更好地从一个例子来探究人口增长过程中的数学。你可能会对下面的研究结果感到惊讶。
一胎只有一个孩子
不像我们的犬科朋友,它们经常一窝可以有好几只小狗,而我们人类通常一胎只有一个孩子。与可以相对自由地决定何时生孩子相比,我们可能会面临这样一个问题:“如果我们已经有了孩子,那么考虑到已有孩子的数量以及孩子们的特征,我们是否应该再要个孩子?”例如,一个恰有2个孩子(都是男孩)的家庭可能会面临这样的困境:一方面,3个孩子可能会太多了,但另一方面,如果能有1个女孩的话,可能会给家庭带来额外的快乐。当然,第3个孩子依然可能还是男孩,如果真是这样的话,那么这个家庭将面临更深的困境。在考虑了所有可能性之后,具有某项特征(此处为性别是女性)的孩子数的数学期望,可能并不会太大(可能只有3或者4)。

图1:人和狗有不同的养育模式。
但是,究竟要靠什么来决定是否继续生育孩子,是依据之前孩子的性别,还是需要考虑因此可能会带来的对人口增长的影响?这个疑问导致了如下的人口问题。
统治者R的需求
人们往往从不考虑解决该问题的过程中对数学家的需求,从而养成了仅靠自己就做决定的糟糕习惯。为了消除这种不便,我们稍微简化一下问题,想象在一个由还不算太差的统治者(注:“Ruler”,简称R)所统治的国家,R有权决定每个女性可以生多少个孩子。然后在某时刻R发现,本国的人口太多了(显然R不属于多余的那些),于是R决定要通过限制女性生孩子的数量来限制人口增长。R知道这样一种措施不会受欢迎,尤其是因为在这个国家,人们更看重男孩(不像上面那段中的那个家庭),并且如果一个家庭只有女孩的话会感到不开心。因此,R希望能确保所有的女性都能得到一个有男性后代的公平的机会。
负责数学问题的部长M的法令
为了达到R的要求,该国负责数学问题的部长(注:“Minister for Mathematical Problems”,简称MMP或M)提出了一个简单的法令:每个女性都可以如她自己所愿地生尽量多的孩子,直到她有了一个男孩为止。显然,因为不能强迫女性去生孩子,所以她们可能没有孩子,也可能在生了任何数量的女孩后,不管出于什么原因,她们决定不再生了。例如,一个女性可以有十个孩子,如果恰巧是先有九个女孩然后有一个男孩或十个全是女孩。但是,不像那个有男孩的母亲,那个有十个女孩的母亲可以自由选择是否生第十一个孩子。
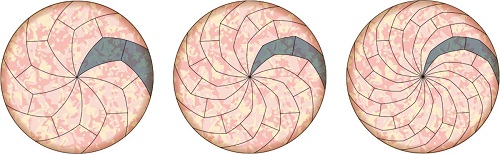
R被M给出的建议弄困惑了,特别是在看到执行这一法令所产生的结果的图解(见下图)之后。看上去,这条规则确实给了所有女性生男孩的公平的机会,但它怎么可能能够抑制人口增长?毕竟,规则的第一部分说,女性可以有尽可能多的孩子,只要她们想要。在下面的卡通图片中有很多的粉色(注:代表女孩)和很少的蓝色(注:代表男孩)。那么,这个规则会不会导致女孩多于男孩吗?以下M将解释为什么不会的原因。
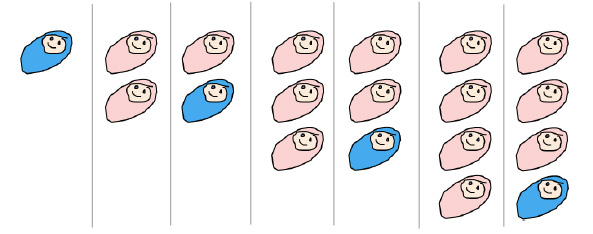
图2.根据M的规则(这里仅考虑不超过四个孩子):可能出现的孩子的组合(每一列是一个可能的组合)(译者注:此处还少一种可能:仅有一个孩子且为女孩;每一列中从上往下的顺序即孩子出生的先后顺序)。
M的解释
如果女性生女孩的概率小于或等于生男孩的概率,那么在孩子们最初的比例中女性将最多只占一半。如果每个女性生育孩子的平均数小于2,那么人口不会持续增长,这是因为给定一代人,不是其中的每个人都能被替代(译者注:这里牵涉到“replacement rate/人口替换率”这一概念。粗糙地说,可以认为人口替换率就是每个女性平均生小孩的个数。先考虑每个家庭:夫妇(这一代)共2人,他们的孩子(下一代)的平均数小于2,然后把所有家庭的情况加起来,就能得出:下一代的人数少于这一代,这也就是上文中“人口不会持续增长”的具体原因)。事实上,生男孩的概率要比生女孩的概率略高(男女孩出生比率约为51:49),因此,即使每个女性平均生育2个孩子,还是会低于人口替换率。(译者注:在下一代中女性的数量会少于这一代中女性的数量,从而导致再下一代的人数减少。)不管怎样,M会把男女孩出生比定为50:50。

图3.抛硬币,50:50的机会生男孩或女孩。
如果该规则意味着女性更容易生出女孩而不是男孩,那么这将给女孩的性别均衡提供支持。然而事实并非如此:根据该规则,对于每个打算继续生下一个孩子的女性,下一个孩子是女孩或男孩的机会依然是均等的,即,都是1/2。于是,对于M而言,很显然女孩并没有变得比男孩更多。每个女性的平均男孩数与女孩数是相等的。(虽然M忽略了某些女性可能会选择流产女胎)。
因为没有一个女性能有超过一个的男孩,所以平均每个女性的男孩数目不能超过一个,同样地,平均每个女性的女孩数目也不能超过一个,给出这样的规则对于性别均衡是没有影响的。所以,平均每个女性的孩子数目最多是2。但是这就最大限度地要求所有的女性成为母亲,并且使每个母亲都有可能需要持续地生无限多个孩子,直到有男孩出生。由于以上条件没有一个可以在实际中发生,所以每个女性的孩子数的平均数目将永远达不到2,因此,人口将不会增长。
然而,R并不相信这种解释并且要求M给出证明。于是,M开始计算:在规则允许的前提下,每个母亲的平均孩子数的最大可能值,请始终记住下面这点:这个值将永远大于实际上的每个母亲的平均孩子数,因为不是所有的女性都会有孩子。此时多胞胎将被忽略,因为这本身就已经是罕见的事件,如果还需要考虑性别并且出现了多于1个男孩的情况那就是更罕见的事件了。
概率
我们记p(1),p(2),……,p(n)依次为一个母亲在其一生中总共有1个,2个,……,n个女孩的概率,g_i为一个母亲已有i个女孩且还想继续生另一个孩子的概率。则(1-g_i)为一个母亲已有i个女孩且不再想继续生孩子的概率。则
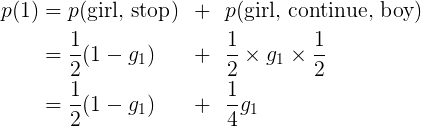
类似地,
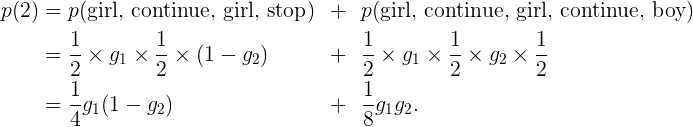
一般地,一个女性一生中恰有n个女孩的概率p(n)是
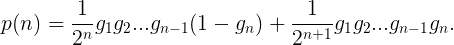
上式等号右边第一项对应于有n个女孩后决定不再生的女性,第二项对应于有n个女孩后又生了一个男孩的女性。
整理上式,得
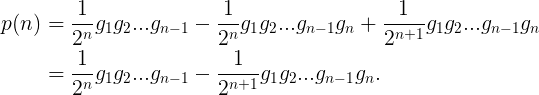
现在让我们转到男孩数上,记q(n)为一个女性有n个男孩的概率。因为女性一旦有了男孩,就不能在生孩子了,所以,对于所有的n>1,有q(n)=0。作为对比,q(1),可由无限多项组成:
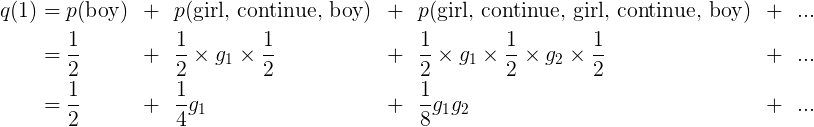
其中第n项是
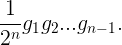
性别均衡
每个女性有的男孩数的均值(期望)是
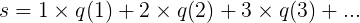
(注:上式原文有误,这里作了订正。 )
其实只需要q(1)这一项,因为所有其它的q(n)都等于0。所以我们有
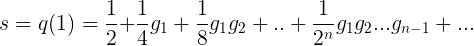
女孩数d的均值是
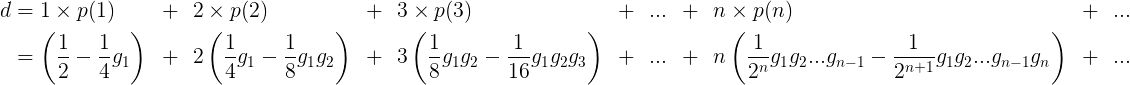
稍微想一下,你可以得到
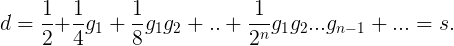
所以,d=s,所以女孩不会多于男孩。
孩子数的均值
我们不知道一个母亲已有给定数量个女孩且还想继续生另一个孩子的概率,换句话说--我们不知道那些g_i的值。然而,我们还是可以按如下方式算出每个母亲孩子数均值的一个上界:第一,任何一个母亲的孩子数都不超过某个数m(例如,为了保险起见,在正常情况下,一个女性不可能有超过100个孩子)。这意味着,g_m = 0。于是现在上式成为如下形式
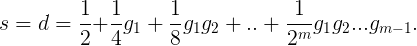
这个平均值依赖于那些g_i的值,当然,当它达到其最大可能值时,所有的g_i(i<m)都等于1,即:无论母亲已有多少个的女孩,总是决定是继续要孩子。(这显然是不现实的,但有助于得到均值的最大可能值。)假设现在就是这种情况,于是
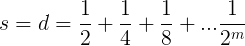
它们的和是
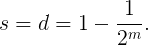
所以,每个母亲孩子数的均值最多为
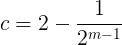
设m>1,我们会发现每个母亲孩子数的均值将永远小于2。而且因为不是所有的女性都会成为母亲,所以每个母亲孩子数的均值甚至会小于c。
现在R相信了,通过禁止已有一个男孩的母亲继续生育,M的规则将限制人口的增长,而且给予每个女性一个能够生男孩的公平合法的机会,同时也并不影响性别均衡。然而,事实上,这个规则只适用于短期使用而无法世代沿袭。因为如果一直沿用该规则,会使人口越来越少。
中国
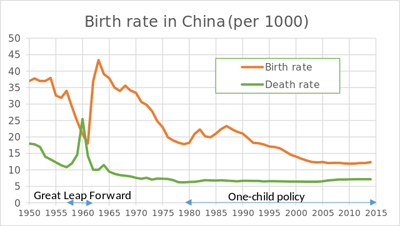
图4.中国的出生率和死亡率。独生子女政策并没有影响所有人口。专家们不确定该政策在多大程度上降低了生育率。图片来源:phoenix7777,CC BY-SA 4。
M的规则看上去可以人为地设计成一个和人们的生活无关的数学问题。但事实上,这个规则是中国部分地区采用的一项政策的延伸部分。直到最近,官方的政策禁止大多数女性生育超过一个孩子,这是一个用来抑制人口增长的严厉措施。然而,许多女性被允许生育2个孩子,如果第1个孩子是女孩,这相当于是一个带有非常小的上界的M的规则的版本(相当于在M的数学推导中,令m=2,这将导致c≤1.5)。在一个众多家庭都偏好男孩的国家里,这给了那些只有一个女孩的母亲又一次生男孩的机会,同时又没有直接改变自然的性别比例,并且使每个女性平均孩子数的均值在所有人口中的贡献小于2。M的规则讲的是,即使所有只有女孩的母亲拥有无穷多次(而不是仅仅只有一次)生男孩的机会,这样人口仍然达不到所需的人口替换率,原因很简单,因为即使女性自己愿意不断生育,但实际上也不可能无限地生育下去。
中国家庭现在已经允许生育2个孩子,而且不论第一个孩子的性别。因为不是所有的女性都会有孩子,也不是所有已有第一个孩子的女性愿意有第二个孩子,所以每个女性的孩子数均值将仍然小于2,所以按照M的规则,也就低于人口替换率。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文