费马大定理:一个傲娇法国人的诡异故事
原文作者,James Propp,马萨诸塞大学数学教授。
译文作者:333,哆嗒数学网翻译组成员,就读于中南大学数学专业。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
这个故事正如数学科普作家西蒙·辛格在一个“数字狂”(Numberphile)视频中所说:这个十七世纪的法国数学家,皮埃尔·德·费马,坐在他的私人图书馆中正读着一本书。他激动地写下了他的一个新发现,就在书的角落里——一个我们如今称为费马大定理,或简写为FLT的断言——但他紧接着写道,书的边角地方太小以至于写不下他的证明。在他还没能跟任何人交流这个问题的细节之前,“他就暴毙而亡了。”
.
关于这个版本的费马大定理故事,我有两个疑问,并且它似乎在暗示是主人公的死亡才导致这个重要的数学秘密被久久尘封。首先,我们看过太多遍“秘密在临死前始终说不出口”的电影片段了;这很做作可笑,不是吗?第二,并没有证据表明费马死前写过那样一段话。我们无法回到过去确定他所使用过的墨水,因为在他的注释被人转录之后原书就不见了,但是从费马的信件中我们能够得知,他读这本书是在职业生涯早期,大约1630年代。大多数学者认为这个传奇的注释写于他死亡之前二十年。所以辛格在他的视频2分15秒开始杜撰了一个过于戏剧性的故事。他仍然确信费马是带着一个没有向任何人揭示的他所声称的证明归于尘土的。

多亏了现代数学家安德鲁·怀尔斯,我们才能够知道费马的声称是正确的,他也因为在费马大定理上的著名工作而在不久前获得了阿贝尔奖。但是,费马真的有那个绝妙的证明吗?这正是我今天想要探讨的。当我们讨论这个费马没有揭示的最著名的证明时,我将要告诉你费马确实创造了一个证明方法——一个可以美妙地解决其它的与此类似形式数论问题的方法。
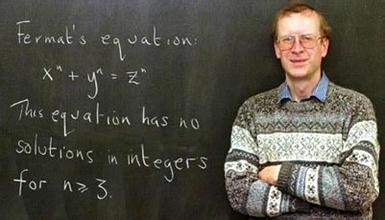
这本使得费马很丢面子的书是他私人抄本的《丢番图算术》。而吸引了费马注意力的那一页上讨论的问题是:将一个平方数分解为两个平方数的和。(5²=4²+3²,20²=16²+12²,再不然分数也行,4² = (16/5)² + (12/5)²,因为丢番图对分数和整数都同样满意。)
费马在书的边上写道:“然而,你却不可能将一个立方数写成两个立方数之和,也不能将一个四次幂数写成两个四次幂数之和,或者更一般的,任何一个高于二次幂的数都不能写成两个和它同次幂的数之和。我已经发现了一个绝妙的证明,但是这里太窄了,我写不下了。”用现代的记号表示即:若n是一个大于2的正整数,则方程x^n + y^n = z^n (x^n 表示x的n次方)没有非零的有理数解(你或许会想为什么我会说“有理数”而不是“整数”?仔细想一想)。费马的儿子在费马1665年去世之后整理出版了父亲的手稿和笔记,才使得这个断言公之于众。
费马是认真的吗?
考虑到费马在今人中的名声很大一部分源自于这个声称,一些人想知道是否有可能他故意误导后世的人们以博得死后的荣耀——他明知这是个困难无比的问题,但在心里察觉到,若他声称有一个办法,那他死后就会像一个无与伦比的圣人那般著名。他的所谓的证明会是纯粹的虚张声势吗?
这是个有意思的观点,但这并不符合我们了解的费马和他那个时代的人。像费马大定理这样的问题并不能激起费马时期那些顶尖的数学家太多的兴趣。微积分正在欧洲文化的子宫里孕育,那些导致了微积分被发明出来的问题才是人们的兴趣所在。费马在解析几何、计算领域、光学、最优化上的创造性工作——正是这些让他享有巨大的声誉。
相反,费马在试图让人们相信诸如他的大定理之类的问题有很大价值时遇到了重重困难。他用以构造“佩尔-费马方程”解的步骤确实引起了一些人的兴趣,比如约翰·沃利斯,但是沃利斯觉得费马否定性的结果索然无味。布莱斯·帕斯卡,他很赞赏费马在概率论上先驱性的工作,然而对费马在数论上的工作却是不屑一顾。
如果我活在费马的时代,我会很同情费马努力所做的工作,但是恐怕我很可能会站在那些怀疑者的一边。我能想象我自己会说:“数学难道不该是解出方程,而不是证明它们无解吗?如果试图找出所有数字解导致我们要去考虑那些压根就没有解的方程,那么从一开始,试图寻找它们的解不就是个错误吗?难道这不是告诉我们费马在问一些错误的问题吗?”
费马敦促他的同时代人在解方程时加入有理性和整数性的要求,并没有其他原因,纯粹是为了使方程更具挑战性。在实数范围内容易解出的方程,在加上诸如有理解或整数解等附加条件后会变得极端困难而精妙。后代人开始视这种精妙为一件好事;这些问题很难但仍然可解的事实表明了这些问题值得研究。随后世纪里最伟大的数学家们,比如莱昂哈德·欧拉、卡尔·弗雷德里希·高斯,对费马的工作非常感兴趣,甚至对他遗留下来未完成的工作更加有兴趣;他们的认可使得费马关于整数谜团的杂乱口袋变成了数学中一个叫数论的分支,并赋予了这个领域自己的合理性和无尚荣耀。应当说明高斯对费马大定理并不感冒,他曾明确指出(在对n=3的情形找到一个证明后)在数论中可以很轻易地提出许多这样很困难的问题。
到十九世纪早期,数学家们已经解决了费马所有的猜想——除了这一个,这也致使这个遗留的问题被冠以“费马大定理”的名号。(不妨告诉你,费马“倒数第二大定理”是被柯西在1813年证明了。)费马声称他关于费马大定理的证明是“绝妙的”给人类知识的鸿沟增添了额外的凄美。
让我们返回十七世纪,费马问题的巨大困难使得很多数学家认为他们应该把心血努力转移到别的地方。正如费马的同代人克里斯蒂安·惠更斯写道,“有别的更好的东西等着我们去做。”所以,要是费马想用不诚实的断言来使人们佩服,那他就不该打费马大定理的主意。
你仍可以刻薄的怀疑,费马的缄默就是他根本没有那个证明的证据。不过你得知道,对于费马而言,对一个命题不给出证明是一件寻常的事,并不是什么例外。他没有发表任何关于数的工作,但他通过和其他数学家的通信来是自己满意。(不错,费马是一个“业余的数学家”,不过话说回来,谁不是呢?)他就像在和他的通信者玩一个奇妙的游戏,他提出一个问题并且暗示如果对方无法解决他就会揭示答案。所以,很有可能费马确有一个关于他的“大定理”的证明,但是在别人绞尽脑汁徒劳无功之前他不愿揭秘,这样就更能显示他自己的聪明。
总之,我从未见过任何可信的证据表明费马在书页边角写下的评注是在误导后人。我认为费马是真的找到了一个论据并且他觉得是一个有效的证明。那绝不是安德鲁·怀尔斯和理查德·泰勒的手段,他们的手段包含了太多的数学新概念(像是“椭圆曲线”)和历代数学研究者的杰出成果,这些都是在费马死后才被发展出来的。数学史专家们认为费马一定拥有一个他自己确信无疑的证明。
如果我们想要理解当费马说他证明了某个数论中的问题时他是什么意思,我们需要了解他用了何种方法。幸运的是,这一点费马能够亲自告诉我们,因为在他一生中,他确实给出了这么一个数论问题的详细证明过程。他使用了一种方法,他认为是他对数论这门学科最重要的贡献:在1657年给皮埃尔·德·卡尔加维的一封信中,费马称其为“无穷递降法”。
无穷递降法
很容易给出一个后项比前项大的无穷正整数序列:如素数序列、完全数序列或者1,2,3,4……但你能想出一个后项比前项小的无穷正整数序列吗?只要稍微想想你就会回答“不可能”。比如,取第一项是一百万,那么第二项至多是999999,第三项至多是999998,一直下去;在一百万项之后(不会更多),这个序列就会发现自己被逼到了角落里,这是因为每一项都要求是正整数。如果第一项不是一百万,是个更大的数,比如十亿,那么这个序列仍然会到达终点,尽管要很多很多项之后。这就是说,不存在无限长的正整数递减序列;无论首项多么大,一个正整数的递减序列迟早都会终结。这个似乎不起眼的费马原理却有着意义深远的结果。
举个例子,让我们把费马的方法运用到这个方程:xy + y² = x² ,我们来证明它没有正整数解。费马会用纯代数的形式来陈述他的证明,而我将采用几何的途径,来使证明的逻辑更清晰。要提醒的是,费马从未将他的无穷递降法用在这样简单的方程上,他发明这个方法是为了敲开更硬的坚果,例如方程x^4 + y^4 = z²,在他给卡尔加维的信中明确的展示了这个方法。
为了开始我们对方程 的分析,首先把“x”用“a”代替,把“y”用“b”代替,这样方程就变成了ab + b² = a²;然后将它变形为(a+b)/a = a/b;接下来将这个方程表示为几何形式,我们可以画一个a×(a+b)的矩形,它里面包含了一个a×a的正方形和一个a×b的矩形,如下图所示。
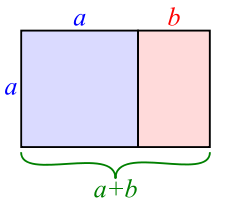
方程(a+b)/a = a/b表明大矩形相似于小矩形:即将大矩形旋转90度,再把它按比例缩小就得到了小矩形。因此,这个大矩形就是古希腊人所说的“黄金矩形”:它包含了一个正方形和其自身的缩小版。同样,这个小矩形也相似于大矩形,它也是个黄金矩形;正如下图所示。所以,这个小矩形也可以分解为一个正方形和一个更小的矩形;这个更小的矩形还能分解成一个正方形和一个更更小的矩形……可以将这个过程一直无限进行下去。
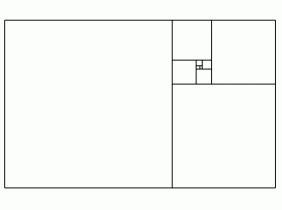
当你第一次看这张图可能会有点眩晕,但这在数学上不成问题。如果从一个黄金矩形开始,你可以画越来越小的正方形和越来越小的黄金矩形,直到你实在没耐心了(或者找不到更尖细的铅笔了)。但是,假如你不是从一个黄金矩形开始会怎么样呢?要是你想徒手画一个黄金矩形,怎么画呢?甚至如果你要求你的黄金矩形每边都是整数个单位长,这又会如何呢?
这样的话,你就陷入了麻烦之中,而费马的无穷递降原理会告诉我们为什么。但是首先,我们需要对图一做一个似乎很天真的观察:如果大矩形的边是整数,那么小矩形的边也是整数(代数语言:若a+b和a是整数,则a和b是整数。这是因为我们可以将b写为(a+b)-a,这是两个整数的差。)为了看出这将导出什么,来看接下去的下面那张图中的小黄金矩形。如果最大的是整数边,那么小的也是,更小的也是,一直下去都是。这样,我们就得到了一个无穷递减的整边矩形序列。看出问题了吗?拿出每个矩形的短边,我们可以得到一个无穷多项递减的正整数序列——但是这是不可能的,这由无穷递降原理可知。所以,不存在一个整数边长的黄金矩形。
间接证明
我们刚刚所展示的证明就是一个间接证明:为了说明某个命题在数学上是不成立的,我们只要说明它的成立会与自身产生矛盾或与已知的产生矛盾即可。举个例子,为了证明不存在整数边长的黄金矩形,我们证明了要是这样的矩形存在就会导致存在无穷递降正整数序列,而这一点与无穷递降原理矛盾。
如果这是你第一次领略非直接证明,你也许会感到有些不安——这仿佛在骗人!如果你这么觉得(有这种感觉很正常),那我告诉你这是一种和我们现实世界并不十分相称的推理方式,在这种推理方式下,事物的性质是受到怀疑的,这样你或许会感觉好一些。这也许就是为什么你的大脑会对这种方法有所警惕。但是在数学中我们处理的是经过精确定义的抽象概念,而不是凭经验的观察所得,因此运用矛盾来证明是一种合理的推理方式。在构建可数数这一数学论据时,我们被允许作出没有无穷递减的可数数序列这一假定——不是因为我们在实际生活中没有遇到这样的序列,而是当我们说可数数时它就已经暗含了这一性质。
如果你认为要是没有间接证明数学会发展的更好,这就有一个问题值得深思:那你还能用什么办法去证明某个东西是不存在的呢?通过遍寻它可能存在的地方然后发现哪儿都没有它?当这样的地方是无限多个时,这种办法就不管用了!
间接证明的一个好处是,在你紧接着的推理过程中提供了非常广阔的目的地:你只要到达其中任意一个矛盾的地方,那就完成了证明。可以把推理的过程想象成地理位置依赖于知识状态的导航过程。如果你试图证明“若命题P,则命题Q”,那么你就会从P出发尝试建立一条通往Q的路线;也许只有惟一一条路线,找到它可能要很高明的技巧。但是,如果你试着去证明命题P和命题Q的否定放在一起可以产生一个矛盾,不管是什么样的矛盾都行,都可以使你到达原来的目的地。你可以马上就试试从一些前提假设作一些随机的结论,再看看它们把你带到了何处!所以这种证明方法经常能给你提供比直接证明更大的前进空间。
如果你喜欢上面那个没有整数边长的黄金矩形的证明,你可以用同样的方法试着证明,不存在五条边和五条对角线都是整数的正五边形。
费马知道什么?他什么时候知道的?
费马有找到了一个正确的证明的可能性,但是这一点随着时间流逝变得越发不可信。因为那些掌握着费马所知道的所有数学工具的业余数学家们,足够聪明也花了足够多的时间在数学上,都没能找到费马大定理的一个初等证明。要是真有那么一个简单的证明,会时至今日还没被发现吗?
大多数历史学家倾向于费马犯了个错误这一观点。(这可能不是他唯一的错误;参看参考列表中的文章“费马的错误”。)这一假设会更可信如果历史学家们能够重现关于费马大定理的那些似是而非的费马式的错误证明。其中之一是费马之后两个世纪,数学家拉梅的那个错误证明;尽管它包含着一些费马那个时代所没有的想法(如将复数引入数论),不过费马很可能有一些基于直觉的、怪异的方法去处理数,而不使用我们今天的方法,比如精巧的三角学方法。所以费马可能有一个天才的方法比拉梅早两个世纪犯了那个错误。
即使没有拉梅的那个例子,我们也能够看出费马是在试图解决一个极其容易犯错的问题。证明一个东西不存在几乎总是要用到间接证明,当你构建了一个间接证明,找出任意一个矛盾就行了。这就使得很容易构建出一个虚假的间接证明:仅仅犯了一个代数错误,就推出了一个矛盾,而这个矛盾却并不能由你最开始的前提假设推出,它仅仅只是起源于你推理中的一个小错误。
大多数对费马的证明抱有兴趣的数学家都得出了和我相同的结论,这也是我在文章标题的选择中所暗示的。这个词组“深夜小狗神秘事件”来自于《福尔摩斯》里的故事《银斑马》,在这个故事里,福尔摩斯向苏格兰警察厅的侦探格雷戈里解释了他的推理。
格雷戈里:“你还有其他东西想引起我的注意吗?”
福尔摩斯:“ 这只狗在晚上的奇怪举动。”
格雷戈里:“这只狗夜里什么都没做。”
福尔摩斯:“那才是一件奇怪的事。”
对于我们而言这个奇怪的事是,在他所有的信件中,包括他1659年最后一封给卡尔加维的信(在这封信中他在总结了他一生在数论中的所做的工作),费马也没有提到他证明了费马大定理。他的确证明了x^4 + y^4 = z²没有正整数解,由此可以推出n=4时的费马大定理成立。费马也声称用他的无穷递降法他也证明了x³ + y³ = z³没有正整数解。但是对于方程x^n + y^n = z^n,当n大于4的时候,他沉默了。是否有可能在他原以为自己证明了费马大定理后,突然意识到实际上他并没有?而他也忘记了在那一页书上重新作个声明,或者他根本就不记得自己写过那段评注?
我们永远也不可能知道真相了,但是除非直到有更多的证据,那似乎是这个数学谜团貌似最真实的答案了。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文