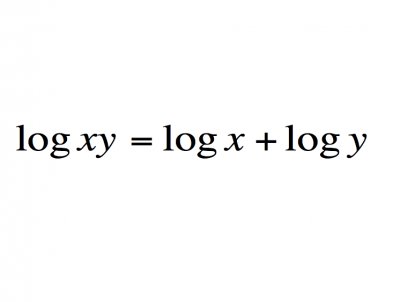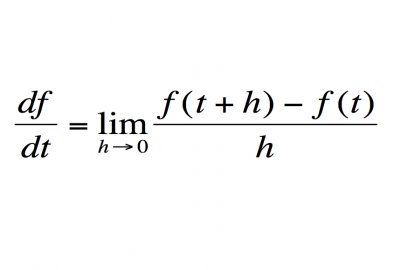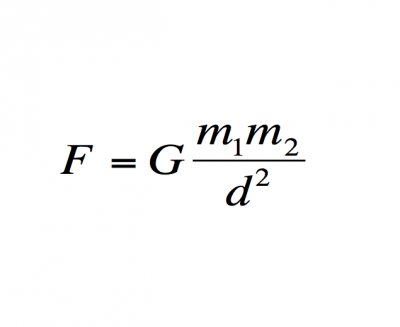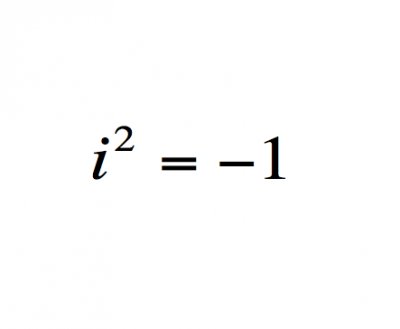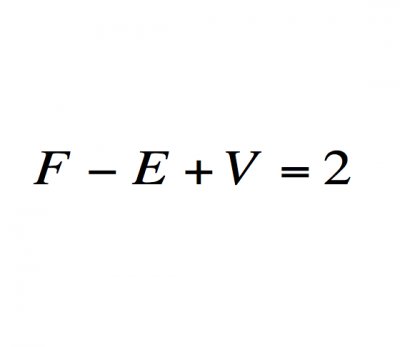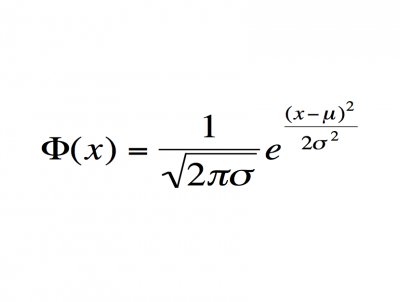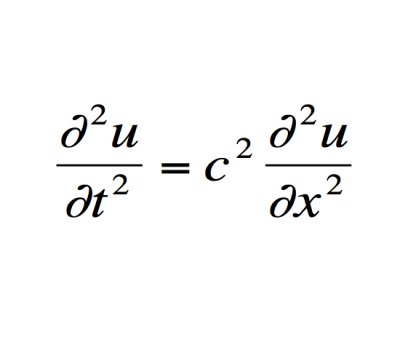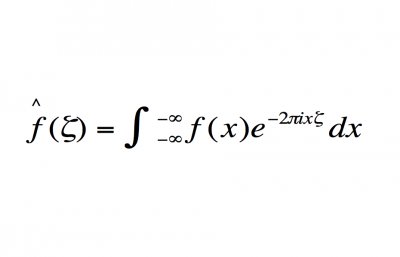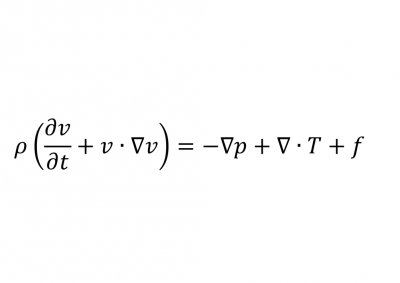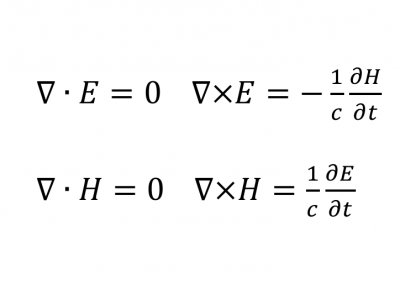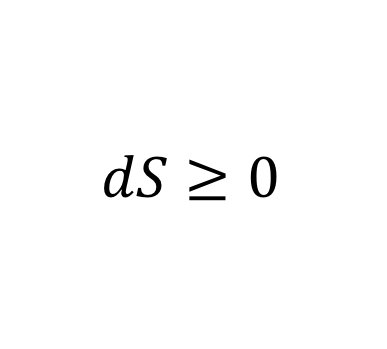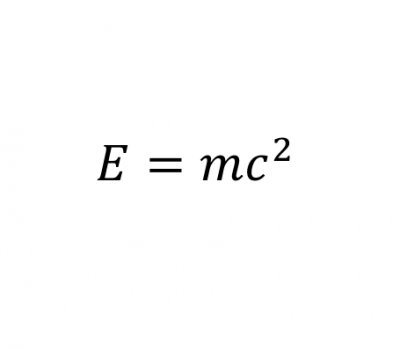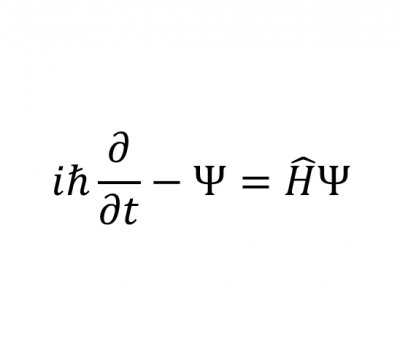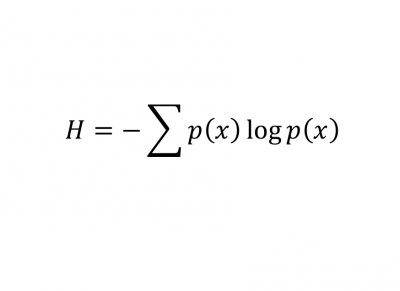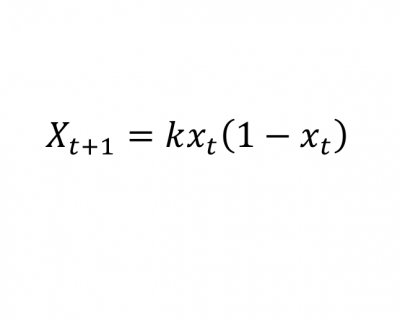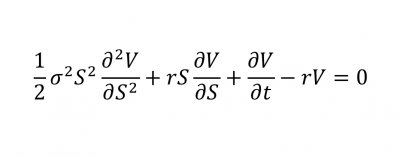0,1,π,e,i就是射雕英雄传中五大高手
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
作者,江苏省徐州市第二十四中学 罗伟
瑞士数学家欧拉是18世纪数学界最杰出的人物之一,他不但为数学界做出贡献,更把整个数学推至物理的领域。他是数学史上最多产的数学家,写了886本书籍和论文,其中有分析、代数、数论、几何、物理、天文学、弹道学、航海学、建筑学等,彼得堡科学院为了整理他的著作,足足忙碌了四十七年。
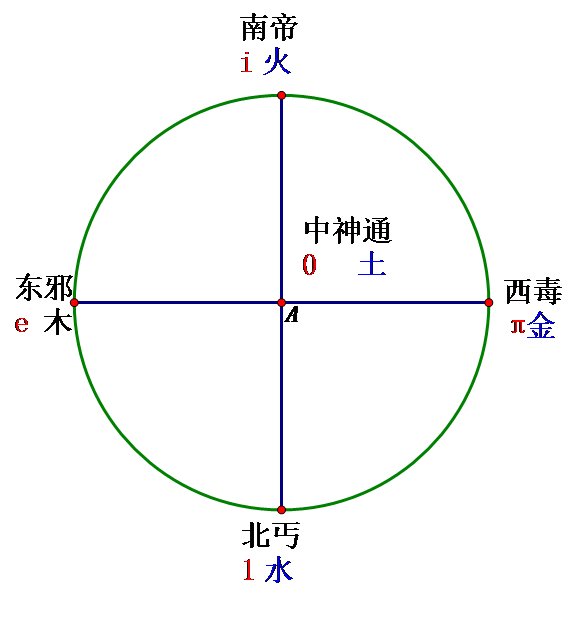
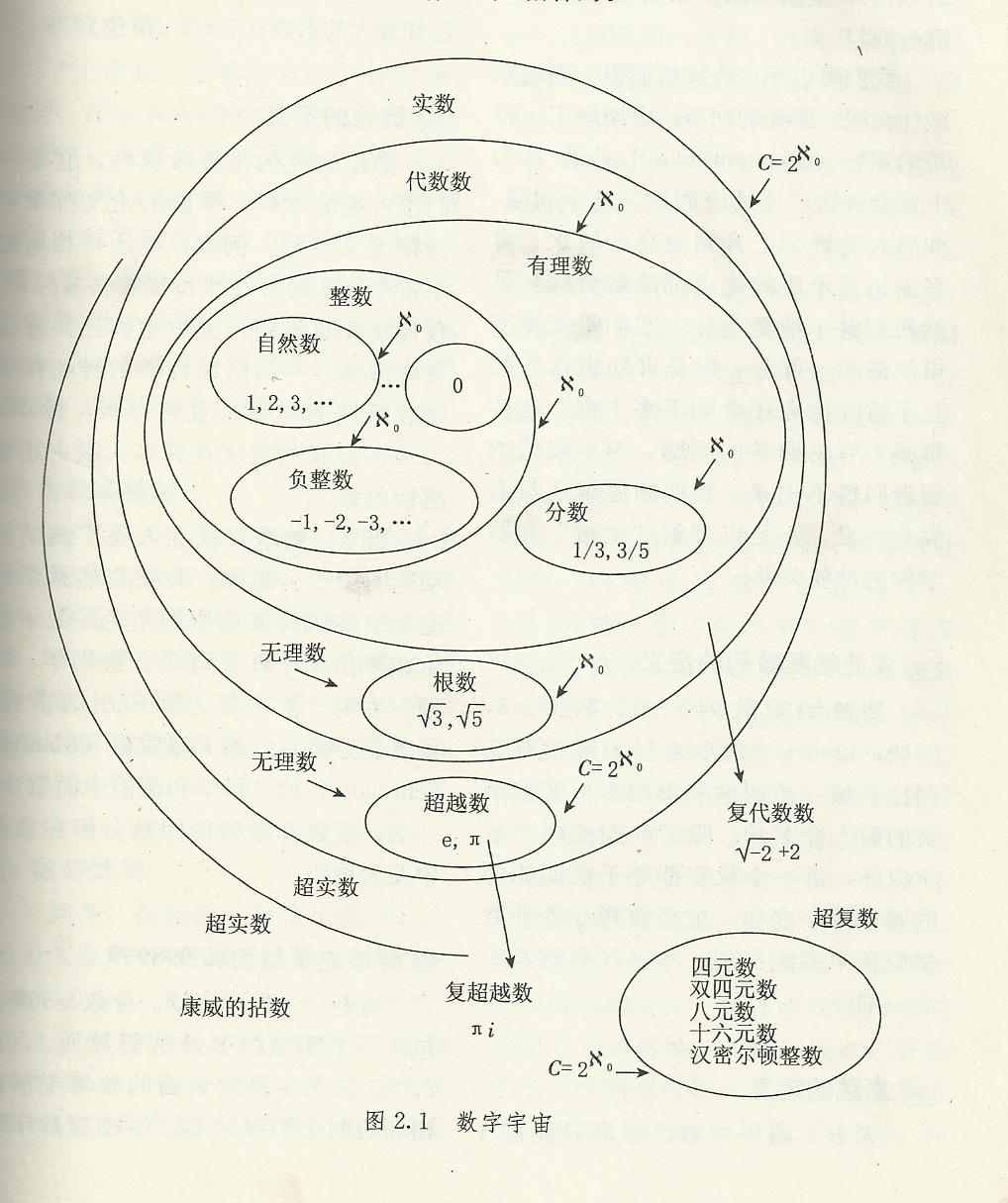
欧拉公式e^(iπ) + 1 = 0中( a^b 表示a的b次方,下同),有五个数,0,1,e,π,i, 其中0,1是有理数,e是自然对数的底,π是圆周率,i 是 -1的一个平方根,体现了数学的一种奇异美。i、e是欧拉创造的,π是欧拉推广的,欧拉把这五个重要的符号用公式统一起来了,可看做数学这颗大树中各个分支的代表,0和1代表算数,i代表代数,π代表几何学,e代表分析学。有朋友要问,欧拉是数学家,怎么和射雕英雄传牵扯在一起呢,我们看过电视剧的都知道,剧中有东邪、西毒、南帝、北丐、中神通五位武林高手,他们也许和数学也有某种联系呢?不信,你听我说说。
一、 东邪----黄药师

首先,这五大高手和五行有关,作者金庸在名字中都有暗示。“东为木”:黄药师三字表面看来似乎有“草”无“木”,其实不然。金庸使用的是繁体字,“药”字的正确写法是“藥”,一根巨木,赫然在下。
正中带有七分邪,邪中带有三分正”的人物,是“桃花岛”的岛主,亦是桃花岛派武学创始人。“桃花影落飞神剑,碧海潮生按玉箫”是他一生武功的写照,造诣非凡,已臻化境,为金庸小说中武功绝顶的高手之一。
黄药师上通天文,下通地理,五行八卦、奇门遁甲、琴棋书画,甚至农田水利、经济兵略等亦无一不晓,无一不精。
e,作为数学常数,是自然对数函数的底数。其近似数约为e = 2.71828182845904523536……,目前为止,已知小数点后约20亿位,也知道是无限不循环小数。
有时称它为欧拉数,以瑞士数学家欧拉命名,欧拉定义如下:
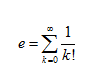
它的另外一个定义是
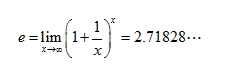
e也为超越数(不为有理系数多项式的根的数)。东邪性情孤僻,行动怪异,身形飘忽,有如鬼魅,算是性格怪异,行动为常人所不解,在常人看来是无理的,漠视“传统礼教”,然却最敬重忠臣孝子个性行事潇洒。又看做超越常人的。e书写流畅洒脱,似弹指神通,又如开创桃花岛一片美景,e^x不论对它微分几次,结果都还是e^x,正如黄药师对他妻子的真情,难怪数学系学生会e用比喻坚定不移的爱情!e又如电脑上网浏览器,我们点击它,可查询古往今来各门学问,都易如反掌。还有一些,你们掌握吗?
e的近似解:培格推导出计算欧拉常数e的公式e≈3-sqrt(5/63)(sqrt表示开根号)。
印度数学家拉马努金的变形公式:
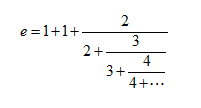
二、西毒-----欧阳锋

西毒欧阳锋——“西为金”:“锋”赖“金”利。作为音乐家的欧阳锋,常备乐器不是吉他,而是铁筝。仍是“金”制。“西,色白”:长居白驼山,他本人、侄儿、部属皆作白衣装。
作为射雕时代中的头号反派人物,只想武功天下第一,使用毒蛇、灵蛇杖法、蛤蟆功等,因逆练郭靖乱改的九阴真经,第二次华山论剑中夺得天下第一。却被黄蓉用计逼疯,跟自己的影子打斗,接着离开华山,后来与洪七公在华山比武,洪七公之功由正转逆,欧阳锋则反由逆转正,两人内力顿时合而为一,水乳交融,一人是在寒冷澈骨时,因对方内力传来而如沐春风,另一人是在全身炙热时,接受对方内力而顿感清凉,两人当下融为一幅“太极之图”。就在时刻,洪七公一跃而起,抱住欧阳锋,说“咱俩殊途同归,最后变成哥俩好”。欧阳锋刹时回光返照,心中一片澄明,与洪七公相拥大笑,两人在笑声中同时辞世。
我们对 要熟悉一些,祖冲之计算出小数点前六位:π= 355/113 = 3.141592 ……,1000年后,西方才把π的值改进。π 是第十六个希腊字母的小写,希腊在西方,π表示圆的周长与直径的比值,也等于圆形之面积与半径平方之比,1736年, 欧拉也开始用π表示圆周率。1974年,人们第一次用计算机来计算π,在运算70小时后,算出小数点后2037位,如今,已算出小数点后万亿位。
π也是无理数和超越数,欧阳锋也算行为怪异,年轻与嫂子私通生下欧阳克,但却只让其叫他叔叔,在《神雕侠侣》中收杨过为儿子,但与东邪比,作恶多端,恩将仇报。一般人不理解。逆练九阴真经;仗着自己的绝世天资与前半生对武学的深厚基底,将所有经脉颠倒移位,练成一种新的厉害武功,越练越怪,越怪越强。因而在第二次华山论剑中夺得天下第一。算是超越完成任务,但疯癫不如常人。π如蛤蟆功,又如灵蛇拳法:手臂犹似忽然没了骨头,如变了一根软鞭,打出后能在空中任意拐弯 。最后和洪七公决斗,恢复神智。两人同归于尽,也算是圆满。
我们可以定义π为满足sin(x) = 0的最小正实数
这里的正弦函数定义为幂级数
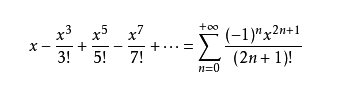
1844年,德国达瑟用不到两个月的时间把π计算到小数点后200位,因超常的计算能力被高斯推荐在汉堡科学院工作。据说,达瑟的计算公式是
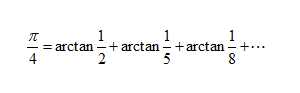
1655年,英国数学家约翰•瓦里斯得到一个π的公式:
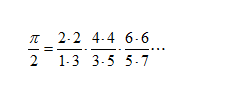
法国数学家维达发现π的公式:
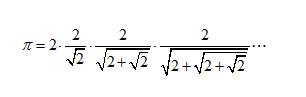
1998年《π》(又译名《死亡密码》)显示了数学人的痴迷。
逆练九阴真经,打通全身静脉的后果,功力大增:
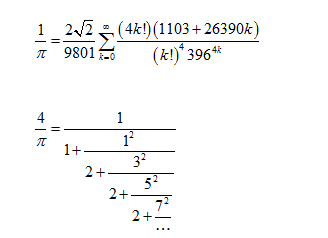
如果东邪西毒合作,会是什么样的情形呢?

拉马努金公式展现无穷级数与连续分数之间的惊人关系,级数和连续分数都可以用π、e表示出来。
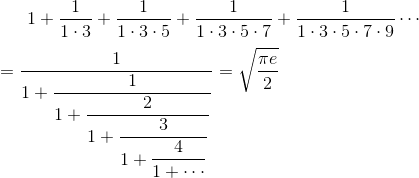
下面一个美得让人惊讶的方程,不仅包括π、e,还包括无理数、阶乘和无穷极限。
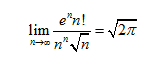
三、南帝----段智兴


南帝,真名段智兴,天龙八部中主角段誉的孙子,大理国的皇帝(如图一),后因故出家,法号一灯(如图二),出自《法华经》:以一灯传诸灯,终至万灯皆明。“南为火”:一灯大师之“灯”待“火”点燃。其秘技为“一阳指”,而太阳是最大的一个火球。“南,色赤”:“灯”与“阳”皆作赤红色。
第一次华山论剑,东邪西毒南帝北丐中神通 五个人大战七天七夜,全真教创始人“中神通”王重阳夺得天下第一, 武林奇书九阴真经被王重阳夺得,其目的是避免天下武林大乱。为防自己死后无人能阻欧阳锋,而在第一次华山论剑的第二年来到大理,用先天功交换了段智兴的一阳指。却不料和王重阳同来的老顽童和段智兴深爱的妃子刘瑛有染,并诞下私生子。不料某一日铁掌帮帮主“铁掌水上飘”裘千仞潜入皇宫并袭击瑛姑之子,瑛姑因而向段智兴求医。而段智兴本欲施救,待打开婴儿襁褓时看到锦帕上刺着“鸳鸯织就欲双飞”;知道自己的皇妃心里仍惦记着周伯通,因而醋意大发。加上他即将要参加华山论剑,而救人将消耗大量功力,犹豫之间,未救而致其死亡。后因心怀愧疚,万念俱灰之下段智兴出家为僧,法号“一灯”。
后来黄蓉身受重伤来到一灯大师住处寻求救治,一灯为黄蓉疗伤,因使用了含有“先天功”的“一阳指”以致元气大伤,后瑛姑来此寻仇。郭靖假扮一灯挡住一刀后,瑛姑才觉悔意。后一灯出现,瑛姑则羞愧而远去。随后与师弟一起翻译了《九阴真经》中总纲的梵文部分,也借助《九阴真经》所载的疗养法门,终得复原功力。
i是-1的一个平方根,在初中阶段,我们知道-1没有实平方根,随着数系的扩大,到高中阶段,由于需要,就产生了i,为虚数单位,且i²=-1,这样数系就由实数扩大到了复数。i看上去就像一盏灯,也像一灯的绝技一阳指,根据五行相克的理论,一阳指最能破解欧阳锋的蛤蟆功,但也不是很容易,要出其不备才有奇效,这才有王重阳装死棺材中重创欧阳锋使其几十年不敢踏中原半步的后话, i名为虚数,如一阳指能治病救人,但要耗费巨大的内力,也如段智兴的心理状态,因愧疚心里不踏实,后又能不断帮助别人。i也像数字1,但没有联通,说明比北丐洪七公看似差一点,但终究有无法跨越的距离。
南帝与西毒的合作可得到πi,其中π是无理数、实数、超越数,i是虚数、复数、代数数,πi是复数、复超越数。
由i拓展也可得到四元数。四元数是一个包含复平面在内的四维空间。可以表示成以下形式:Q = a + bi + cj + dk ,其中i,j,k都是三个互相垂直方向上的单位向量(与虚数i一样),他们都和实轴垂直,两个四元数相加或相乘,可以看成是关于i,j,k的多项式,按照下面的规律产生如下结果:
I² = j² = k² = -1
ij = -ji = k jk = -kj = i ki = -ik =j
四、北丐----洪七公

北丐洪七公 “北为水”:七公姓“洪”,果见洪水汤汤,“北,色黑”.书中不曾描写七公衣服颜色。但他作为丐帮老头子,估计不管衣服原色为何,上身之后,必将改造成唯一色调:总是黑。(从图看,有点不对,毕竟是天下第一帮丐帮帮主吗,也要注意点形象。)
洪七公为丐帮帮主,为人正义且机智,生性贪吃,曾经因贪吃误事,自断其右手食指,故也称"九指神丐",无论黑白两道都十分敬重他。在桃花岛,洪、黄、欧阳三人以音乐比试武功,岛主吹箫,欧阳弹筝,老七公没得钱买乐器,只好鼓着两片腮帮子作“仰天长啸”状,实为艰苦朴素、廉洁自律之典范。洪七公和蔼正义,具有一切正派人物所应具有的优点,一直率领丐帮抗击金兵。其独门武学为"打狗棒法"及"降龙十八掌"。
洪七公一生最大的敌人为"西毒"欧阳锋,曾被其暗算多次,几乎丧命。晚年与欧阳锋于华山比武,两人打了四日,总之是打得神困力倦,几欲虚脱,斗过棍棒,休息了一下,两人接著又比拼内力,结果竟战到天下两个均已奄奄一息。两人隔天又开始比起了纸上谈兵,比法是洪七公按招式逐一告诉杨过打狗棒法,杨过演给欧阳锋看,欧阳锋再思考破解的杖法,两人拆解了三天,到第三日欧阳锋已破解打狗棒法的前三十五路,而打狗棒法的第三十六路天下无狗,这一式则让欧阳锋思考到一夜之间须眉尽白,似乎老了十多岁,这才将之破解。后比试内功,耗尽功夫,欧阳锋恢复记忆,两人大笑,互相拥抱而逝。
数字1给洪七公,数字1和0是自然数、有理数、实数,看上去很自然,是实实在在存在的,天下第一就是这个1字,首先,丐帮为天下第一大帮,对外用降龙十八掌抗击金兵,对内用打狗棒除暴安良、劫富济贫,洪七公为人善良,就是面对老毒物遇到危险差点被火烧,也冒着生命危险去救他,满满的正能量。
数学上,你知道1有什么特殊的用处吗?
三角函数的变换很多都离不开1。
南帝和北丐同为首领,1和i在一起,组成了更广阔的一片新天地,那就是任何复数都可以由二者表示出来。
z=a•1 + b•i,其中a、b为实数
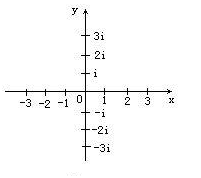
虚数可对应平面上的纵轴,与对应平面上横轴的实数同样真实。虚数轴和实数轴构成的平面称复数平面,复平面上每一点对应着一个复数。
东邪、西毒和北丐在一起
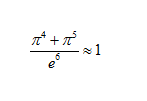
五、中神通----王重阳

中神通王重阳——‘中央为土”:原名“王喆”,这姓名两个字皆具“土”形。 “中央,色黄”:王重阳既为道教大师,而道士用黄冠束发,因此又被称作“黄冠”。
王重阳少年时曾大举义旗,与金兵对敌,但因不遗余力,动用数千人力,历时数年建成“活死人墓”,在其中暗藏器甲粮草,作为起事之根本。由于将士伤亡殆尽,王重阳愤而出家,自称“活死人”,后来生平劲敌林朝英在墓门智激王重阳,二人,化敌为友,携手同闯江湖。
林朝英对王重阳甚有情意,欲以身相许,但王重阳以国事为重,不谈私情, 两人本已化敌为友,后来却又因爱成仇,约在终南山上比武决胜,斗了几千招,始终难分胜败。
最终林朝英和王重阳打赌,石头上刻字,胜过王重阳,逼使他在出家为道士与跟她一起在古墓中长相厮守之间作一选择。但王重阳宁愿把自己所建的古墓让给她居住,自己另在古墓不远处盖了全真观,出家为道士,那就是重阳宫。而后道书读得多了,大彻大悟,乃苦心潜修,功成丹圆后,前往山东布教,建立全真道,先后收马钰、孙不二、丘处机等七人为弟子,后世称“全真七真人”。
王重阳得知林朝英在活死人墓中逝世,想起她一生对自己情痴,悲痛万分,于是悄悄从密道进墓,见到两间石室顶上她的遗刻的玉女心经,招招克敌全真武功,后精研这玉女心经的破法,终未成功。
后来武林奇书“九阴真经”出现在江湖中,引起各路武林人士争夺。华山论剑,力压四强,天下第一,王重阳因此夺得九阴真经。他决意不练经中功夫,但为好奇心所驱使,禁不住翻阅一遍。一经过目,思索上十余日,即已全盘豁然领悟,后回到活死人墓,在最隐秘刻下九阴真经的要旨,并一一指出破除玉女心经之法。
王重阳旧疾复发,为了在身死之后留下一个克制西毒欧阳锋之人,求段智兴传他一阳指,以先天功作为交换,后来王重阳假装病死,以一阳指破掉了欧阳锋的蛤蟆功,使得欧阳锋退回西域。王重阳也在此之后逝去。
王重阳和洪七公都有义举,曾抗击金兵,以国家为重,所以在五大常数中只有0和1供选择,才有切实意义,王重阳的武功第一,缘于研究玉女心经,夺得九阴真经后,自己禁不住翻阅,有违当初华山论剑不研习九阴真经功夫之嫌,虽然没传授全真七子相关功夫。然世界还算相对公平的,黄药师、洪七公、一灯大师都练过九阴真经或运用之疗伤来恢复功力,欧阳锋也逆练九阴真经,武功达到新高。在射雕英雄传中,王重阳已经故去,对他的描写只是残存在部分人的回忆中,所以用0来表示以为最佳。
在数学中,你知道0有什么妙用吗?
学生们曾被教授0的任意次幂都是0,但是很多时候认为0的0次幂是未定义的(部分数学书把0的0次幂也规定成1,比如陶哲轩的实分析——编者注)。如果你要画出x^y的示意图的话,你会看到在点(0,0)是不连续的。关于0的0次方的应该是多少的讨论已经很久了,这个争论曾风行整个19世纪。
中神通与北丐的组合:
任何一个不等于0的数的0次幂都等于1,这就相当于人们纪念中神通这一天下第一武林高手。
20世纪被称作第三次科技革命的重要标志之一的计算机的发明与应用,因为数字计算机只能识别和处理由0、1符号串组成的代码。其运算模式正是二进制。0、1是基本算符。非常简单方便,易于用电子方式实现。
还有一个式子,你理解吗?
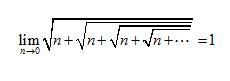
问世间是否此山最高
或者另有高处比天高
在世间自有山比此山更高
欧拉不仅包含科学创见,而且富有科学思想,他给后人留下了极其丰富的科学遗产和为科学现身的精神。历史学家把欧拉同阿基米德、牛顿、高斯并列为数学史上的“四杰”。如果数学家也能来一次华山论剑,相信欧拉也是绝顶高手之一。
参考文献:数学之恋 克利福德•A•皮科夫 注 马东玺 译 湖南科学技术出版社
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文