原文作者:陶哲轩,加州大学洛杉矶分校数学教授,2006年菲尔兹奖得主。
译文作者:念琦,哆嗒数学网翻译组成员,就读于东北师大附中。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
新浪微博:http://weibo.com/duodaa
注:以下是对我做了一些评分工作之后产生的新想法和有关计算的记录。这个类型的问题可能已经在某些文献中被研究过了;我很乐意了解任何相关的资料。
假设一次考试中有N道判断对错题,每道题的答案是随机的,即答案是“对”和“错”的概率相等,并且不同的问题之间没有关联。假设参加考试的学生必须用“对”或“错”回答每一道题(不允许跳过任何一道题)。
那么我们很容易知道如何评分:只要数一数每个同学正确回答了多少道题(也就是每道题回答正确得一分,回答错误不得分),并将这个数字k作为考试成绩即可。
更普遍的情况是,我们将每道回答正确的题的得分记为A,每道回答错误的题的得分记为B(通常是一个负数),那么总分将是 Ak+B(N-k)。只要A>B,这种评分方案就相当于对前一种直接把k作为总分的模式进行了改变比例的变换,并且同样可以达到评价学生和鼓励学生尽可能多地正确回答问题的目的。
然而事实上,学生很可能不能绝对确定每个问题的答案。
我们可以采取一个概率模型,即对于一个给定的学生S和一个给定的问题n,学生S认为问题n的答案为“对”的概率是p(S,n),而答案为“错”的概率是1-p(S,n),其中0≤p(S,n)≤1,p(S,n)可以被看作一个衡量学生S对这个问题的答案的自信程度的量(若p(S,n)趋近于1,则S对于答案是“对”有信心,反之若p(S,n)趋近于0,则S对于答案是“错”有信心);为了简化问题我们假定在这个概率模型中,每个问题的答案都是相互独立的随机量。
考虑这个模型,并且假设学生S希望最大化自己的得分,我们很容易发现S回答问题的最优策略是当p(S,n)>1/2时回答“对”,当p(S,n)<1/2时回答“错”。(如果p(S,n)=1/2,S可以任意选择答案。)
[注意:这里的“自信程度”不是统计学中的术语“置信度”,而是一个描述主观概率的非正式用语。]
就现状来说这样还不错,但是对于评估学生究竟掌握知识到何种程度的目的,它只提供了一些有限的信息,尤其是我们不能直接看到学生对每道题的自信程度p(S,n)。
举例来说,假设S在10道题中回答正确了7道,那是因为他或她确实知道这七道题的答案,还是因为他或她对这十道题作出了合理推测,使得最终的正确率略高于随机猜测的正确率而达到70%呢?看起来如果学生只被允许回答“对”和“错”,我们没有办法辨别这两种情况。
但如果学生可以给出概率性的答案呢?也就是说,对于给定的问题n,学生不是只能回答“对”或“错”,而是可以给出一个如“答案是‘对’的可能性为60%”(因此答案是“错”的可能性为40%)的回答。这样的回答使我们更加了解学生掌握知识的程度;更重要的是,理论上我们将可以确切地知道学生对每道题的自信程度p(S,n)。
但是现在,如何评分变得难以确定了。假设100%确信正确答案的回答得一分,60%确信正确答案的回答应该得多少分?60%确信错误答案(等同于40%确信正确答案)又应该得多少分?
数学上,我们可以选择评分函数f:[0,1]→R,当学生对正确答案给出的可能性为p时,得分为f(p)。例如,如果学生认为“对”的可能性为60%(因此“错”的可能性为40%),在这个评分方案下,如果正确答案是“对”,学生的得分为f(0.6),如果正确答案是“错”,得分为f(0.4)。我们的问题是:在这种情况下最合适的函数f是什么?
直观地,我们认为f应该单调递增——对于正确答案有较高自信的学生应该得到比对正确答案自信较低学生更高的分数。另一方面,后一种学生也应该得到一部分分数。一种想法是采用线性的函数f(p)=p,即对正确答案给出60%自信的学生将得到0.6分。但这是最好的选择吗?
为了使这个问题在数学上更明确,我们需要一个客观的标准来评价评分方案。这里可以采用的一种标准是是否避免了不正当奖励。
如果一个评分方案设计得不好,学生最终可能会夸大或故意少说自己对答案的自信程度,以此提高自己的(期望)成绩:对于一个学生,一道题的最优回答q(S,n)可能与其主观的自信程度p(S,n)不同。因此我们可以设计一个总能使得q(S,n)=p(S,n)的评分方案,从而激励学生真实地写下他或她对此题的自信程度。
这是对评分函数f的一个明确约束。如果学生S认为问题n的答案为“对”的可能性为p(S,n),答案为“错”的可能性为1-p(S,n),而作答时回答答案是“对”的可能性为q(S,n)(因此“错”的可能性为1-q(S,n)),学生对这道题得分的期望为
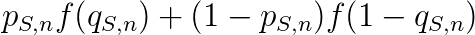
为了使这个期望最大化(假设函数f可导:在一个部分给分的评分方案中这是一个合理的假设),学生会执行对独立变量q(S,n)求导并使结果为零的策略,得到
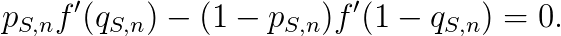
为了避免不正当奖励,期望的最大值应在q(S,n)=p(S,n)时取到,因此我们有
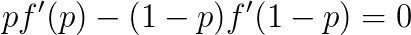
对于所有0≤p(S,n)≤1成立。这要求函数p→pf'(p)为一常量。(严格地说,应是要求函数p→f'(p)关于p=1/2对称;但是如果将问题推广到不止两个选项的多选题的情况,对于只与正确选项的自信程度有关的评分方案,同样的分析将得出pf'(p)必为一与p无关的常量的结论;这个计算留给感兴趣的读者完成。)
也就是说,f(p)应为Alogp+B的形式,其中A,B为常数;根据单调性,A为正数。如果我们规定f(1/2)=0(即“对”和“错”的自信程度各占50%时不得分)以及f(1)=1,我们就得到了评分方案
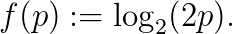
因此,如果一个学生认为答案是“对”的可能性为p,答案是“错”的可能性为1-p,如果正确答案是“对”,他或她将得到
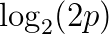
的分数,如果正确答案是“错”,他或她将得到
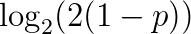
的分数。下表中的值可用于说明这种评分方案:
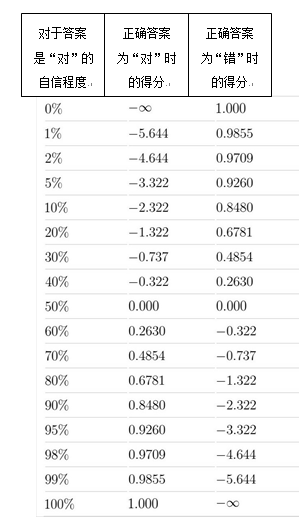
我们注意到对于错误答案自信程度很高时惩罚会很严重;尤其是,学生会避免回答对某个答案有100%的自信,除非他或她真的绝对确信自己的答案。
在这个评分方案下,若学生S对每个问题n的回答是答案为“对”的可能性为p(S,n),答案为“错”的可能性为1-p(S,n),则总分为
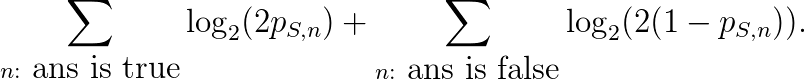
这个分数也可以被写作
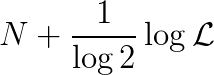
其中,
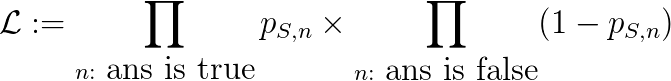
是给定正确答案的情况下学生S的主观概率模型(即学生S的答案)的似然函数。因此这里的评分系统还有一种对数似然函数的解释。它激励学生使自己的主观概率的正确可能性最大化,这与统计学中的标准做法(最大似然法)一致。
根据贝叶斯概率的观点,学生的分数可以被看作对学生的主观概率模型为正确(接近正确答案)的后验概率比先验概率高出多少的(对数尺度下的)量度。
我们可以用上述的评分方案评估对二元事件的预测,例如对于即将到来的只有两名候选人的选举,就可以在事后看看各预测者的预言起了多大作用。
这样做会遇到的一个困难是很多预测都不会给出一个明确的概率,而如果对任何并非完全确定的预测给出了默认100%的主观概率,只要其中任意一个预测错误,就必然产生-∞的得分。
但是如果预测者拒绝给出明确的概率,或许我们可以设计一个默认的主观概率p,并且(选择一些合适的该预测者做出的预测作为“训练样本”)找到使该预测者得分最高的p值。这个值作为默认概率可以被用于该预测者此后做出的任何预测。
以上的评分方案很容易推广到多选题的情况。但是我遇到的一个困难是如何处理不确定性,也就是学生甚至无法给出一道题的答案为“对”或“错”的可能性的情况。
这时,允许学生空题(也就是回答“我不知道”)是很自然的;更加高级的选项是允许学生以一个自信程度的区间作答(例如“我认为答案为‘对’的可能性在50%到70%之间”)。
但是对此我还没有一个很好的评分方案;一旦学生的主观概率模型中出现不确定性,由于“不确定的不确定概率”,最大化学生分数的期望的问题就会是不适定的,因此之前使用的判断是否避免了不正当奖励的标准也不再适用了。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
新浪微博:http://weibo.com/duodaa



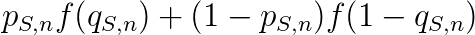
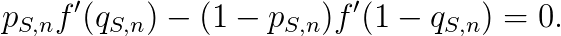
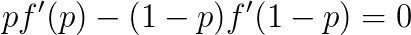
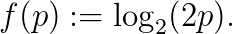
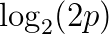
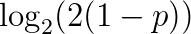

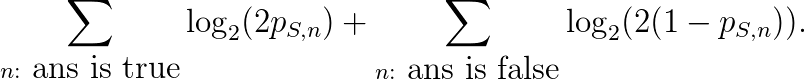
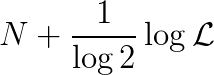
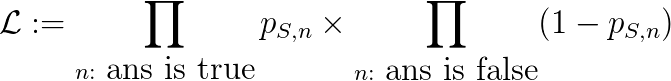



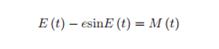 (1)
(1)
 (2)
(2) (3)
(3) (4)
(4)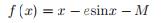 (5)
(5)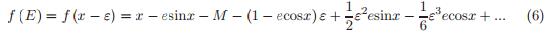
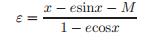 (7)
(7)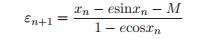 (8)
(8)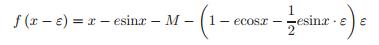 (9)
(9)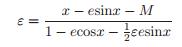 (10)
(10)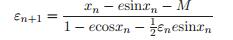 (11)
(11)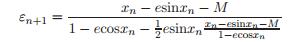 (12)
(12) (13)
(13) (14)
(14)  (15)
(15) (16)
(16) 和
和  (17)
(17) 和
和  (18)
(18)