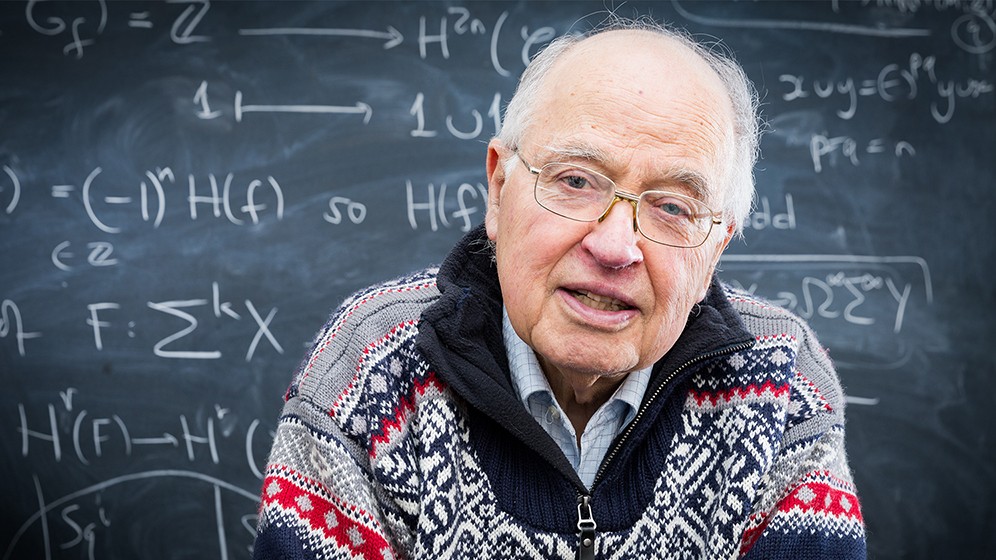原文作者:Siobhan Roberts,专注于数学与科学的记者。
编译作者:Mathyrl ,哆嗒数学网翻译组成员,软件工程师。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
新浪微博:http://weibo.com/duodaa
尽管迈克尔·阿蒂亚(Michael Atiyah)的许多荣誉 ——他是菲尔兹奖和阿贝尔数学奖得主; 世界上最古老的科学团体伦敦皇家学会的前任主席(以及爱丁堡皇家学会的前任主席);剑桥大学三一学院的前主任; 爵士和皇家勋章的成员;并且基本上是英国的数学教皇 --- 但也许对他最贴切的描述是一个媒人。他有一种直觉来安排恰当的知识联络,通常涉及他自己和他个人的想法。在他半个世纪多的职业生涯中,他弥合了数学领域以及数学和物理中截然不同的想法之间的鸿沟。
例如,2013年春天的一天,当他坐在白金汉宫的女王画廊,等待与伊丽莎白二世参加年度皇家勋章午宴,阿蒂亚爵士为他的终生的朋友和同事、伟大的数学物理学家罗杰·彭罗斯(Roger Penrose)爵士做了一次“媒”。
彭罗斯一直在试图发展他的“扭量”理论,一条已经进行了近50年的指向量子引力的道路。 “我有一种办法,这意味着走向无穷,”彭罗斯说,“先试图在那里解决问题,然后再回来。”他认为一定有一个更简单的方法。然后,阿蒂亚马上指出了它,建议彭罗斯使用一种“非交换代数”。
“我想,‘哦,我的上帝,’”彭罗斯说。 “因为我知道这个非交换代数在这里一直在扭量理论里面。但我没有想到以这种特殊的方式使用它。有些人可能刚刚说,‘那样做不行的’,但是阿蒂亚可以立即看到,你可以用一种方法使它工作,那正是正确的做法。”考虑到阿蒂亚提出建议的地点,彭罗斯称他的改进的想法“宫殿般的扭量理论”。
这就是阿蒂亚的力量。大致来说,他花了他的职业生涯的前半部分将数学连接到数学,后半部分将数学连接到物理。
阿蒂亚最为人所知的是“指标定理”,于1963年和麻省理工学院的艾沙道尔·辛格(Isadore Singer)(正确地称为阿蒂亚-辛格指标定理)证出,该定理连接分析和拓扑 --- 这是一个被证明在数学领域以及后来的物理学中都很重要的基本联系。很大程度上由于这项工作,阿蒂亚获得了1966年的菲尔兹奖和2004年的阿贝尔奖(与辛格)。

在20世纪80年代,从指标定理中收集的方法意外地在弦理论的发展中发挥了作用 --- 试图将大尺度下适用的广义相对论和引力与小尺度下的量子力学相协调 --- 特别是在新泽西州普林斯顿高级研究所的弦理论家爱德华·威腾(Edward Witten)的工作中。威腾和阿蒂亚开始了深入合作,并在1990年威腾获得了菲尔兹奖,他是有史以来唯一获得该奖的物理学家,阿蒂亚是他的拥护者。
现在,86岁的阿蒂亚几乎没有降低标准。他仍然在研究大问题,仍然在试图统一量子和引力。在这方面,想法快速而激烈地到来,但正如阿蒂亚自己所描述的,它们仍然是直观、富有想象力、模糊和笨拙的原料。
尽管如此,他还是喜欢这种自由流动的创造力的状态,紧凑的时间表给他增添活力。在追求这些当前的调查和思考的过程中,去年12月,他在爱丁堡大学同一天里连续发表了多场的讲座,自1997年以来,他一直是爱丁堡大学的名誉教授。他热衷于分享他的新想法,他希望吸引支持者。为此,在11月,他在爱丁堡皇家学会举办了一个关于“美丽科学”的会议。在皇家学会集会和随后,每当他放慢下来有充分的时间,Quanta杂志就和阿蒂亚坐下来向他提问。以下是这些能抓多少就抓多少的对话的编辑版本。
QUANTA杂志:你对美和科学的兴趣的起点在哪里?
阿蒂亚:我出生86年前。那是我的兴趣开始。我母亲在佛罗伦萨怀上了我。我的父母要给我取名叫米开朗基罗,但有人说:“这对于一个小男孩来说是一个很大的名字。”这将是一场灾难。我不能画画。我根本没有天赋。
你提到了在罗杰·彭罗斯的“艺术在数学中的作用”的演讲中有什么东西“豁然开朗”了,你现在有了一个合作论文的想法。这个豁然开朗的过程或状态 --- 你能描述一下吗?
是这样一种东西:一旦你看到它,真相或真实性,它只是盯着你的脸。真相回过头来看你。你不必去找它。它在上面闪耀。
一般你的想法就是这样到来吗?
这是一个引人入胜的版本。数学的疯狂部分是当一个想法出现在你的脑海的时候。通常当你睡着了,因为这是你最无拘无束的时候。这个想法从某处浮起,天知道在哪里。它漂浮在天空中;你看看它,并欣赏它的颜色。它只是在那里。然后在某个阶段,当你试图冻住它,想要把它放在一个坚实的框架,或使它面对现实,然后它就消失掉,它不见了。但它被一个结构所取代,结构捕捉了某些方面,但这是一个笨拙的解释。
你总是做数学方面的梦吗?
我想是这样。梦想发生在白天,它们发生在夜间。你可以称它们是一个幻象或直觉。但基本上它们是一个思想状态 --- 没有词,没有图片,没有公式或语句。它是“先于”所有这些。它先于柏拉图。这是一个非常原始的感觉。再次,如果你试图抓住它,它就会死去。所以,当你早晨醒来时,一些模糊的残留物萦绕着,一个想法的幽灵。你试着想起它是什么,你只能得到一半正确的它,也许这是你能做到最好的了。
想象力是它的一部分吗?
绝对是的。在想象中进行时间旅行是易如反掌的 --- 你甚至不需要买票。人们回到过去,想象他们是大爆炸的一部分,然后他们问之前提出的问题。
是什么引导想象力 ——是美吗?
这不是你可以说明的那种美丽 --- 它是一个更抽象意义上的美。
不久之前,你与 泽米儿·泽基(Semir Zeki),伦敦大学学院的神经生物学家和其他合作者发表了一篇关于数学美及其神经相关的体验的研究。
这是我写过的最多人读的文章!很久以前人们就知道,当你听到好的音乐,阅读好的诗歌,或看到好的图片时,大脑的某些部分会亮起来 --- 所有这些反应都发生在同一个地方(“情感大脑”,特别是内侧眶额叶皮层)。问题是:数学美的欣赏是一样的还是不同的?结论是,它是一样的。大脑在音乐,艺术和诗歌中欣赏美的相同部位也参与数学美的欣赏。这是一个大的发现。
你通过向数学家展示各种方程,同时功能性磁共振成像(fMRI)记录他们的反应得到这个结论。哪个方程最漂亮?
啊,最漂亮的是欧拉公式:
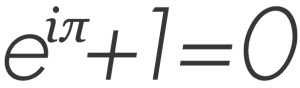
它涉及π;数学常数e [欧拉数,2.71828 ...]; i,虚数单位;1;和0 —— 它在一个公式中结合了数学里所有最重要的东西,这个公式真的很深刻。所以大家都同意这是最美丽的方程。我曾经说过,这是哈姆雷特的名句“生存还是毁灭”(To be, or not to be)的数学等价 ——非常短,非常简洁,但同时非常深刻。欧拉方程只使用五个符号,但它也包含了美妙的深刻的想法,简洁是美丽的重要组成部分。
你因两个极其漂亮的工作而非常知名,不仅是指标定理,还有与德国拓扑学家弗里德里希·希策布鲁赫(Friedrich Hirzebruch)发展的K理论。跟我讲讲K理论。
指标定理和K理论实际上是同一枚硬币的两面。它们开始不同,但之后它们变得如此地融合在一起以至于你不能解开它们。它们都与物理学有关,但是以不同的方式。
K理论是对平坦空间和平坦空间移动的研究。例如,让我们拿一个球体,地球,让我们拿一本大书,把它放在地球上并移动它。这是一个平坦的几何体在一个弯曲的几何体上移动。 K理论研究这种情况的所有方面 --- 拓扑和几何。它源于我们对地球的导航。
我们用来探索地球的地图也可以用来探索大规模的宇宙,用火箭射出到太空,和小规模的宇宙,研究原子和分子。我现在正在做的是试图统一所有这一切,而K理论是做到这一点的自然的方式。我们已经做了这种类型的地图数百年,我们可能会一直做数千年。
你对于K理论和指标定理在物理学中被证明是重要的感到意外吗?
噢,是的。我做了所有这些几何,没有任何它将链接到物理的想法。当人们说,“嗯,你所做的与物理学联系起来了。”这是一个大大的意外。所以我快速学习物理学,与好的物理学家交谈,以了解发生了什么。
你和威腾的合作是怎么产生的?
我在1977年在波士顿认识他,当时我对物理和数学之间的联系感兴趣。我参加了一次会议,有这个年轻的小伙子和老家伙们。我们开始说话,几分钟后,我意识到,年轻的小伙子比老家伙们更聪明。他理解我所说的所有数学,所以我开始注意他。那是威腾。我从那时起就一直和他保持联系。
和他一起工作是什么体验?
2001年,他邀请我去加州理工学院,在那里他是一位客座教授。我感觉像是再次成为一个研究生。每天早上我都会走进系里,我去会见威腾,我们会聊一个小时左右。他会给我做家庭作业。我会走开,花23个小时来赶上。同时,他会下去做半打其他的事情。我们有一个非常激烈的合作。这是一个令人难以置信的经验,因为这像和一个高明的导师一起工作。我的意思是,在我想到答案之前,他已经知道所有的答案。如果我们曾经有过争论,那么他是对的而我错了。真是尴尬!
你之前说过,在数学和物理之间偶尔出现的意想不到的互连是最吸引你的 --- 你喜欢发现自己闯入陌生的领域。
对的; 嗯,你看,很多数学是可预测的。有人向你展示如何解决一个问题,你再次做同样的事情。每次你向前迈进一步,你都会遵循前面那个人的步骤。每一次,有人提出了一个全新的想法,惊动了大家。刚开始,人们不相信它,然后当他们相信它,它导致一个全新的方向。数学之道是断断续续的。它有持续的发展,然后当突然有人有一个新的想法,它有不连续的跳跃。这些是真正重要的想法。当你得到它们,它们有重大的影响。我们还会有另一个跳跃。爱因斯坦100年前有一个好主意,我们需要另一个来带我们前进。
但是该方法不能只有引导性,还必须更具有研究性。如果你试图引导科学,你只能让人们走你告诉他们去的方向。所有的科学都来自人们注意到有趣的侧面路径。你必须有一个非常灵活的探索方法,让不同的人来尝试不同的事情。这是很困难的,因为除非你随大流,否则你不能得到一份工作。
由于担心前程,你必须守规矩。这是现代科学最糟糕的事情。幸运的是,当你达到我的年龄,你不需要管这一点。我可以想说就说。
这些天,你正在尝试一些新的想法,希望打破物理学的僵局?
嗯,你看,原子物理——电子,质子和中子,所有构成原子的东西。在这些非常非常非常小的尺度上,物理学的规律是相同的,但也有一个你忽略的力,这是一个引力。重力存在于任何地方,因为它来自宇宙的整个质量。它不会自己消失,它没有正值或负值,它都叠加起来。因此,不管黑洞和星系有多远,它们在宇宙中的任何地方都施加了非常小的力,即使在电子或质子中也是如此。但物理学家说,“啊,是的,但它是那么小,你可以忽略它;我们不测量那么小的东西,没有它我们也做得很好。”我的出发点是,这是一个错误。如果你纠正这个错误,你会得到一个更好的理论。
我现在再看一下大约100年前的一些想法,当时被丢弃了,因为人们不能理解它们。物质如何与重力相互作用?爱因斯坦的理论是,如果你放入一点物质,它改变了空间的曲率。当空间的曲率变化时,它对物质起作用。这是一个非常复杂的反馈机制。
我要回到爱因斯坦和保罗·狄拉克,用新的视点再次看着他们,我想我看到了人们错过的事情。我正在填补历史的空白,考虑到新的发现。考古学家挖掘东西,或历史学家找到一个新的手稿,并提供了一个全新的思想。这就是我一直在做的。不是去图书馆,而是坐在我家里的房间里,思考。如果你思考了足够长时间,你会得到一个好主意。
所以你的意思是引力不能忽略?
我认为物理学家所有的困难来自于忽略它。你不应该忽略它。关键是,我相信,如果你引入它,数学会得到简化。如果你离开它,你使自己更困难。
大多数人会说,当你看原子物理时,你不需要担心引力。规模很小,对于我们所做的计算,它可以忽略。在某种意义上,如果你只是想要答案,这是正确的。但是如果你想要理解,那么在这个选择中你犯了一个错误。
如果我错了,好吧,我犯了一个错误。但我不这么认为。因为一旦你选择这个想法,有各种各样的好的结果。数学融合在一起。物理学融合在一起。哲学融合在一起。
威腾对你的新想法怎么看?
好吧,这是一个挑战。因为在过去当我和他谈到我的一些想法时,他认为它们没有希望,他给了我10个不同的理由为什么它们是无望的。现在我想我可以捍卫我的想法。我花了很多时间思考,从不同的角度来看,并回到它。我希望我能说服他,我的新方法是有价值的。
你冒着损失声誉的风险,但你认为这是值得的。
我是作为一个数学家建立的声誉。如果我现在把事情弄糟,人们会说,“好吧,他是一个好的数学家,但在他的生命的尽头,他失去了他的骄傲。
我的一个朋友,约翰·鲍金霍恩(John Polkinghorne),就像我正在做的一样离开物理; 他进了教堂,成了一个神学家。在我80岁生日我们进行了讨论,他对我说,“你没有什么可失去的; 你只管前进,按你的想法去思考。”这就是我一直在做的。我拿到了我想要的所有奖牌。我能失去什么?所以这就是为什么我准备赌一把,这是一个年轻的研究员不会准备做的。
你在这个职业生涯的这个阶段对充满新想法感到惊讶吗?
我的一个儿子对我说,“不可能,爸爸。数学家在他们40岁的时候做完他们所有最好的工作。你年过80. 现在你不可能有什么好想法。
如果你在80岁以上的时候仍然保持清醒和警觉,你就有了优势:你已经活了很长时间,你已经看到很多事情,你有视角。我现在是86岁,在过去几年里,我有了这些想法。新的想法来了,你东一个西一个地捡起来,现在时机成熟了,而5年或10年前时机可能还没成熟。
是否有一个大问题一直在引导着你?
我总是想尝试理解为什么事情行得通。我不想只知道一个公式而不知道它是什么意思。我总是试图挖掘背后的东西,所以如果我有一个公式,我明白为什么它在那里。而理解本身是一个非常困难的事情。
人们认为数学开始于你写下一个定理,然后给出一个证明。这不是开始,而是结束。对我来说,数学创造性的地方,在你开始把事情写在纸上之前,在你尝试写一个公式之前。你画各种东西,你在你的头脑把它们翻转。你正在试图创建,就像一个音乐家试图创造音乐,或一个诗人。没有规定。你必须以你自己的方式做。但最后,就像一个作曲家必须把它放在纸上,你必须把东西写下来。但最重要的阶段是理解。证明本身并不能让你理解。你可以有一个很长的证明,最后不知道为什么它行得通。但要了解为什么它行得通,你必须对它有一种直觉反应。你必须感觉到它。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
新浪微博:http://weibo.com/duodaa








 ,
,