数学与统计学竟如此不同
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
原文作者,Bai Li,就读于多伦多大学计算机科学学院。
翻译作者,豆浆,哆嗒数学网翻译组成员。
校对,小米。

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
原文作者,Bai Li,就读于多伦多大学计算机科学学院。
翻译作者,豆浆,哆嗒数学网翻译组成员。
校对,小米。





关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Patrick Honner,美国杰出数学和科学教育总统奖得主。
翻译作者,radium ,哆嗒数学网翻译组成员。
校对,mathyrl。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
在刚开始理解什么是数学家和物理学家眼中抽象的对称结构,我们得先从熟悉的形状开始。
你得原谅数学家被魔群深深的勾住,一个如此巨大而神秘的代数对象吸引他们花费接近10年的时间去证明它存在。现在,三十年后,弦理论家们——也是正在研究所有的基本力和粒子如何通过在隐藏维度振动的微小的弦来解释的物理学家——发现魔群与物理学中的深刻思想有联系(研究出来的主要定理可以解释魔群的量子场论构造,事实上魔群是一种特殊弦论的对称群)。
这个元素个数的数量级达到10的53次方,并且同时让数学家和物理学家兴奋的集合是什么?在建立新的物理理论中搞清对称性的数学结构以及隐藏的对称性的过程中,像魔群这样的代数群的研究提供了线索。
群论在很多方面集中体现了数学的抽象性,但是它构成了一些我们的大部分类似于数学经验的基础。现在让我们研究对称性的基础以及阐明他们代数结构。
我们喜欢说一个事物具有对称性,但是它真正的含义是什么呢?直觉上讲,对于像镜像那样的事物,我们有对称的感觉。假设我们画一条垂直的线穿过正方形的中间。
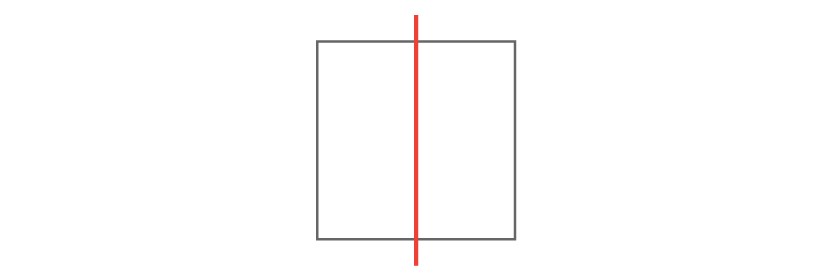
这条线将正方形分成两个相等的部分,这两部分互为对方的镜像。这个熟悉的例子被称为轴对称。但是这儿还有其他与镜像无关的对称类型。
例如,正方形还具有旋转对称性。
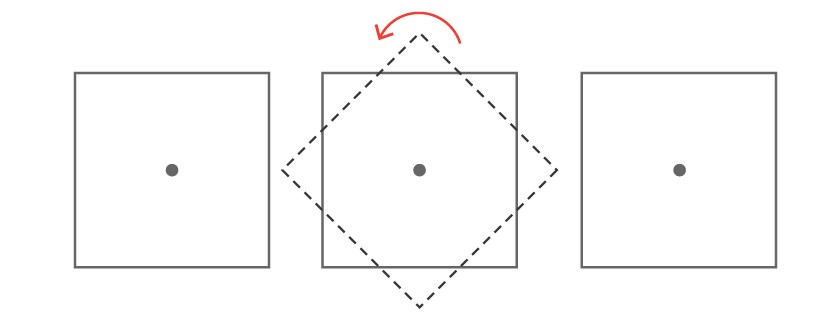
从这个例子中我们可以看见正方形关于它中心点(对角线的交点)逆时针旋转的过程。在旋转了90度(四分之一的翻转之后,它看起来和之前的一样。
我们定义一个对象变换是对称的,如果这个物体变换后与变换前的形状一样。上述旋转是正方形对称性的一种,而我们轴对称的例子可以作为第二种对称性。
让我们花一点时间来定义一些的术语。我们将称最初的对象为“原像”,而变换后的对象为“像”。我们将用术语“映射”去描述从一个对象(一个点,一个线段,一个正方形,等等)变换到另一个对象的过程。对称性要求变换不改变对象的大小或者形状。
一个变换如果满足这样的要求被称为“等距”,或者称作刚体运动。基本的等距变换是关于一条线反射,关于一个点旋转,以及沿着一个向量平移。
现在我们继续分析正方形的对称性。我们知道有一种对称性是“关于一条通过中心的垂线反射”;另外一种是“关于中心逆时针旋转90度”那么还有其他的吗?他们是什么?还有多少种?在数学中经常出现这样的情况,提前规定好的记号将让我们的分析更加容易。
首先,假设我告诉你我已经通过对称性变换好了正方形,下图是结果。

这样的结果应用了那种对称性?旋转?反射?当然这不可能精确地看出来运用了哪种对称的准则。为了帮助我们确认具体应用了哪对称性,让我们从标记原始正方形的顶点开始分析。
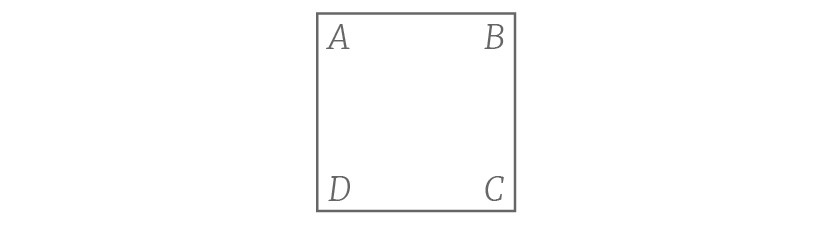
进一步,让我们规定不论何时我们描述原始正方形都用这样的标记:左上角为A,右上角为B,右下角为C,以及左下角为D。
好了,现在我们开始变换正方形,我们可以追踪标记是怎样移动的。例如,在关于一条过中心的垂线反射后,正方形变成了下面这样的形式:
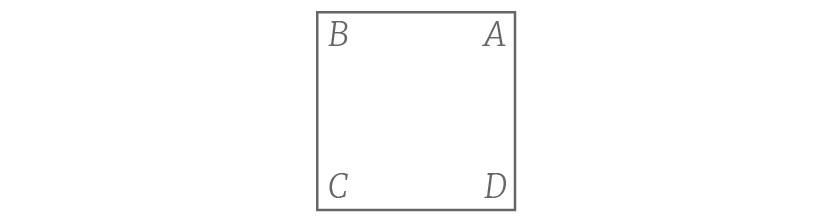
对比原始的标记,A现在在B的位置,而B在最初A的位置。类似的,C和D也交换了位置。将原始标签作为ABCD,我们将经过变换后新的标签记为BADC。
这样就清晰地揭示了,在这样的变换下,A被映射成了B,B被映射成了A,C被映射成了D,最后D被映射成了C。我们可以可视化记号是怎么变换的:

我们将一直记原始位置为ABCD,因此列表中的相对位置描述了每个原始顶点在变换下映射的位置。在另一个例子中,我们绕中心逆时针旋转90度可以标记为DABC,在这个变化中A被映射成D,B被映射成A,以此类推。
严格的来说,这仅仅描述了在一次变换中每一个顶点发生了什么。但事实证明,这足以描述整个正方形变换的情况。这是因为对称变换是等距的,因此维持了对象的大小和形状相等。
等距不能让尖角或顶点变平,因为那样将会变对象的形状。这意味着所有的角A,B,C,D都将映射成角。类似的,等距变换的性质保证了线段将映射成线段。
于是,一旦我们知道正方形的角往那边走了,相应的边也沿着相同的路线行走。换句话说,正方形边的像决定于对应端点的像。
这就意味着我们能完整的通过排列四个字母A、B、C和D具体说明正方形的一个对称。这本身是非常好的,但它同时也立即暗示着正方形对称的形式的数量有一个上界。正方形对称形式的种数不超过四个字母排列组合的种数。那么有多少种排列呢?
考虑用这些字母创造一个排列,你可以从这四个字母中的任意一个字母开始,但是一旦你选择了一个字母,那么对于第二个字母你就仅仅只有三种选择。一旦你选择了第二个字母,在第三个字母上你就只有两种选择,最后,对于第四个字母将你只有一种选择。一个基本的计数方式告诉我们有
4 × 3 × 2 × 1 (= 4!) = 24
4 ×3×2×1(=4!) = 24种可能的排列。因此,对于正方形这儿最多有24种对称方式。
事实上,正方形的对称形式远少于24种,一个简单的论据将告诉我们为什么。让我们回到原始图形。假设我们知道正方形的一个对称把A映射成B,那么C又如何呢?
答案很明显,C只能被映射到D上去。A和C是正方形对角线的端点。因为等距不改变长度,A和C的距离必须和映射前的距离相等。如果A映射成了B,那么现在与A的距离等于对角线长度的唯一对应点D就是点C必须到达的地方。
这样就极大的减少了正方形对称性可能的数量。假定我们构造了一个对称,那么A点有多少种可能性?因为顶点必须对应到顶点上去,关于A的映射这儿仅有四种可能的情况。一旦我们选择了一种方式,那么A的对角线端点C的映射也只有一种方式。那么对于B就只有两种选择了,类似的方法我们可以知道D也只有一种选择。
notation:
最后,讨论正方形的对称性,我们真正需要考虑的只有两种情况:A点的选择方式(四种)以及B点的选择方式(2种)。这就意味着这儿仅仅只有4 × 2 = 8 种可能性。这儿用我们的记号列出了完整的清单:

现在我们无法保证所有的八种可能性都是正方形实际对称性。但是它是一个小的列表,所以我们可以逐一验证它。实际上他们都是合法的对称性:左边的四种是旋转对称性(旋转角度为0°,90°,180°,以及270°)右边的四种是轴对称(两个关于过中心的垂线和水平线对称,两个关于对角线对称)。
所以这八种变换都是对称性,我们已经确定了正方形最多有八种对称性,显然我们已经把它们全面找到了。但这真的就是全部的情况吗?
当我们发现一种自然的方式去组合对称方式,一个新的关系产生了:我们可以简单的应用他们在一系列变换在中(一种称为“复合”变换运算)因为应用对称性再次给了我们一个一样的正方形,你可以应用另一个对称性再次产生一个一样的正方形。
这就意味着如果你连续应用多个对称性,这些对称性的复合本身是也是正方形的对称性!我们可以通过上述八种的各种组合造成新的对称性。
但当我们试图这样做时一些有趣的事情发生了。假设我们逆时针旋转正方形90°然后让沿过中心的垂线反射,那么顶点会发生什么变化呢?
旋转让A变成D,然后经过反射到C,所以最终是A到C。B旋转到A,然后反射回到B,所以B映射到B。C旋转到B,然后反射到A,然后D旋转到C,然后反射回D。在我们采取的记号中,这些两次变换的复合可以被描述为:

但是这个对称都已经在我们的列表里面了!逆时针旋转90°后通过中心的垂线反射,实际上就是关于对角线BD做了一次反射。事实上,每一次上述八种对称性的组合本身也就是上述八种对称性之一。
现在我们已经在这些对称性集合中揭示了基础的代数内在结构。当我们通过组合两种对称性时,我们得到了另一种对称性,用一样的方式我们通过加法结合两个数字得到另一个数字。而恒等对称(旋转0°)在我们数字系统中表现为数字0.
而每一个对称性都可以被抵消,就像加三也可以加上-3来抵消:例如,正方形旋转90°可以被再旋转270°抵消。
这是群基本的代数属性,他们赋予群,就像正方形对称性的集合,具有类似于我们熟悉的数字系统的结构和规律性。但是对称性的群也展现了他们自己的复杂以及微妙的特征。
例如,我们关于正方形的对称群仅仅包含八个元素,与我们无限的数字系统形成了鲜明的对比。当我们能组合对称性在一定程度上相似于我们叠加数字,我们组合的顺序导致不同的结果,例如:3+4=4+3但是在旋转之后反射与在反射之后旋转结果却不同。
由简单的正方形对称性,我们已经对代数结构有了一种模糊的感觉,那么你是不是想知道数学家和弦理论学家研究的魔群深处的是什么了?
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
美国数学会评选的年度数学热门事件又来了,今年的晚了一些,大家来看看吧。

玛丽安・米尔扎哈尼,1977年5月3日——2017年7月14日

菲尔茨奖的唯一女性获奖者玛丽安・米尔札哈尼在今年7月14日去世了,年仅40岁。 米尔札哈尼是斯坦福大学的教授。她是一位极具原创性的数学工作者,对几何和动力系统领域作出了许多重大贡献。她的工作连接了几大数学方向——包括双曲几何、复分析、拓扑和动力学——反过来她的工作也深刻地影响了这些方向。世界各地的媒体都报告了她的生活和数学贡献。
《隐藏人物》,电影与数学家

电影《隐藏人物》在2016年12月发行前就得到了大量曝光。2017年1月AMS年度数学联合会上,本书作者 Margot Lee Shetterly和参与了美国航空工程的数学家 Christine Darden出席了该电影的发布会,现场座无虚席。2017年,电影明星在电视节目上谈论那些激励人心的女数学家故事,书本和电影引起了读书俱乐部的关注,学校组织学生去电影院,甚至还出现了一套以电影中的女性为主题的商标--这些都被媒体广泛报道。在2017年5月,美国航天局把其在弗吉尼亚州汉普敦Langley研究中心的一栋大楼以97岁女数学家凯瑟琳・强森的名字命名,用以表达她的敬意。
丹尼尔·罗思曼关于生物大灭绝的研究

麻省理工大学的丹尼尔·罗思曼教授在《科学进展》杂志上发表了名为《预测下一次生物大灭绝或全球灾难时间的数学公式》的论文。这无疑是一个沉重的话题。论文引起了广大媒体的关注。
数学与“杰利蝾螈”现象
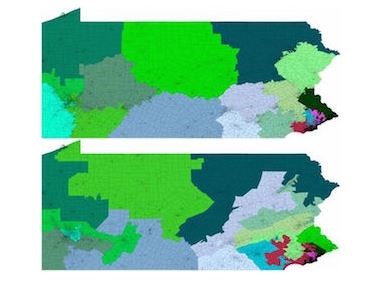
2017年夏天,数学家Moon Duchin在塔夫茨大学组织了一个度量几何与“杰利蝾螈”研究小组,旨在用新的数学工具分析和解决杰利蝾螈现象。(图:宾西法尼亚州一种可行的选区划分方案,它将整个州黄划分成为18个人口相等的选区。下图:宾州现行的选区划分。)
恩尼格玛密码机被拍卖

“一台罕见的纳粹二战期间使用的恩尼格玛密码机周二在拍卖会上以45,000欧元被一名匿名网上买家买走。”CNN报道。正如史密森尼学会指出,“这台恩尼格玛机是有史以来出镜最多的密码机。”这种机器在二战期间被德国军方改造用来加密信息,而盟军最终破译了这种密码——这是在2014年电影《模仿游戏》中讲述的故事。许多版本的恩尼格玛机都成为了收藏品,而这台被拍卖的恩尼格玛机格外引人注目,原因是它的主人在当初在跳蚤市场上只用100欧元买下了它。
维拉尼当选法国议员

43岁的数学家、菲尔茨奖得主赛得里克·维拉尼,在南巴黎的一次选举中赢得了69%的选票并成为了一名新的法国国民议员。在《科学》杂志的一次采访中,维拉尼说到,“我从未计划参与任何国家政治活动。但马克龙的政党对欧盟热情的支持,这在法国国家政党中是非常罕见的。它同时也反对过去的政治传统,即在选举中系统地攻击对手;相反地它倡导博爱、实用主义和进步。同时,他的政党也欢迎非政治家的专业人士。”
《数学杀伤性武器》

凯西·欧尼尔这本书的副标题是“大数据加剧了不平等并威胁了民主”。无论是在电台还是纸媒的采访中,欧尼尔都强调人们并不理解数学模型、算法以及打分系统如何在生活的方方面面影响了我们——大学录取、监狱系统、就业、保险、选举、棒球队招募、社交网格、金融系统和教育。在EdSurge的访谈中她谈到,“算法,说白了就是一种打分系统。只要你有了一个打分系统,你就可以钻系统的漏洞。漏洞钻得多了,系统就不再有效了。这就是现实。”
伊夫·梅耶尔获得2017阿贝尔奖

今天3月,挪威科学和文学会宣布伊夫·梅耶尔获得今年的阿贝尔奖,以表彰他“为小波分析的数学理论发展中做出的突出贡献。”阿贝尔奖是数学界中最有威望和慷慨的奖项之一。这则新闻被各大新闻和科学媒体报道,包括《自然》、《福布斯》、《卫报》、《法国商业报》、《爱尔兰时报》、《科学美国人》等等。
Urschel从橄榄球生涯退役成为一名职业数学家

作为一巴尔的摩乌鸦队的一名职业橄榄球运动员同时也是麻省理工一名数学研究生,Urschel因为他的双重份已经被媒体报道多年。2017年他决定在26岁的年纪从橄榄球生涯退役专攻数学。就在近日,一份报告揭露了橄榄球运动中广泛存在的运动员大脑损伤,但Urschel说他的决定更多地是为了更好地研究他的数学。
媒体达人尤金妮娅·郑

尤金妮娅·郑 把烘焙和高维范畴学结合在了一起。她对于数学及其与音乐、烘焙和日常生活联系的热情是充满感染力的——这是她为什么出现在许多的电视广播节目与出版物中。“数学是奇妙的,而我们也必须以一种奇妙的方式去对待它。”
π节

每年的π节(3月14日)都吸引了很多媒体的眼球。大量的故事和语音都在探讨它的历史、庆祝、相关的难题、游戏(想象呼拉圈和悠悠球),当然还有如何烹制派。学生和数学家们——今天还有美国航天局——都加入到这些向π致敬的有趣的活动中。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
