原文作者,Dr. Dilts,俄勒冈大学数学博士。
翻译作者,风无名,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
哥德尔的不完备定理是那种能把你脑浆敲出来的一个定理。

在上一篇博客,我们讨论了定理本身及其影响。简单说来,它们显示出了数学本身的内在局限性。
哥德尔第一定理与一致性、可证明性这两个概念有关。一个数学系统(由一些假设组成,这些假设被称作是“公理”)称为一致的,如果它们没有矛盾存在。换句话说,你不能证明一个既真又假的语句。
在任何逻辑系统内,都有很多语句,也就是那些你能说出的东西。比如,我像这样说“所有的素数都比十亿小”。它是一个错误的语句,但是我仍能说出它。

但是,仅仅因为我能说出一个语句,并不意味着我可以证明它为真或者假。大多数情况下,那个语句是难以证明的,所以你不知道如何证明它。可是,还有一种可能,存在既不能证明为真,也不能证明为假的语句。这种语句,我们称为不可证明的语句。任何拥有不可证明语句的逻辑系统(公理集)成为不完备的。
哥德尔第一不完备定理说了:如果你有一个一致的数学系统(也就是,一堆互不矛盾的公理),并且你可以做算数运算,那么,一定存在使用那些公理不能证明的语句。[原注1]
换句话说,数学是不完备的。证明所有的事情,是不可能的。(译者注: 笼统地说数学是不完备的,是不对的。此文作者这里提供的是一个不严谨的简单说法。)
哥德尔第一不完备定理的最基础的想法,就是这句话:“这句话是不可证明的”。
如果你能证明这句话是正确的,根据定义,它就是可证明的。但是这句话自己说了它是不可以证明的;同时由于它是真的,它也是不可以证明的。但是它不能既是可证明的又是不可证明的。因此,这句话必须只能是不可证明的。
虽然这就是我们将来采用的基础的想法,问题是,在数学里面,并不存在一个明显的形式化的方法来说“这句话是不可证明的”。你说的可证明是什么意思?“这句话”指什么?使用什么公理呢?
哥德尔的证明必须让所有的这些都完美的严格化。
第一步要证明的是:任何严格的数学语句都可以转化为一个数,反过来也可以。

这一步是精妙的,不过并不复杂。从某种意义上说,这就像一段代码,它把每一字母都转化成一个数。比如,我们可以这样做:a转换成1,b转换成2,等等。单词”math"将会转化成"13-1-20-8"。计算机也使用了类似的模式来把文本存储像成0和1的形式。
为了把数赋给严格的数学语句,哥德尔使用了类似的方法来进行编码。实现这种编码的方式并不唯一,不过我将要讲一种与哥德尔最初的方法比较接近的方法。

第一步,对于你的某个数学系统的每一个数学符号,给予一个数。[原注2]比如,也许”0"被存储为1, “=”被存为储2, "+"存储为3.
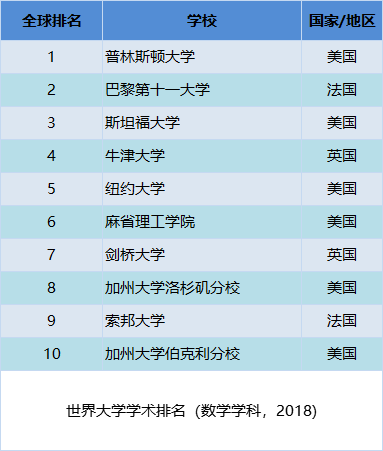
一条数学语句就是这些符号的一个列表。使用数对单个的符号进行编码,就可以等价地说,语句就是数的列表。例如 0=0等价于(1,2,1)。
为了把语句编码为唯一的数,我们让它的哥德尔数等于一部分素数的幂的乘积,幂的次数为数学符号在列表中的位置。因此,0=0的哥德尔数是2^1 · 3^2 · 5^1 = 90。
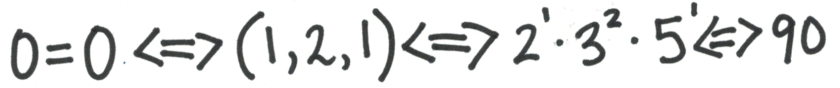
对于一个语句S,比如”0= 0”,我们使用记号G(S)来指代它的哥德尔数。因此,G(0=0) = 90。
正如你意识到的,即使是对中等长度的语句,哥德尔数也会很快变得非常大。不过,大小不是一个问题,我们不需要把它们写下来,你只需要知道这样的数存在就可以了。

关键的问题是:对于任一个数,我们可以返回来得到一条数学语句。
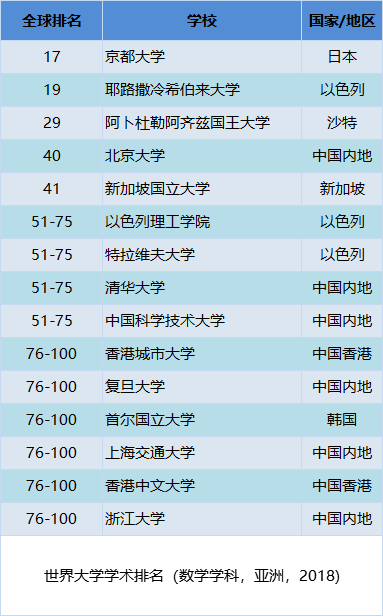
每一个数都可以唯一地分解为素数的乘积。如145530 = 2^1 · 3^3 · 5^1 · 7^2 · 11^1,所以145530代表了 0 + 0 = 0.
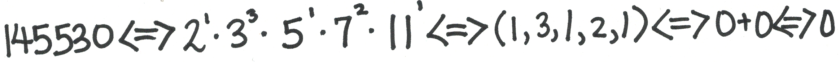
任一严格的数学语句都可以用这种方式翻译成一个数。乃至一个证明,也仅仅是一些捆绑在一起的语句而已。(“A” 蕴含“B”, 并且“B”蕴含“C”,所以“A”蕴含“C”)。那就意味着,我们展示了所有的数学都能够仅用数来写出来。[原注3]
类似地,存在一个算数的方法来检查一串使用哥德尔数来表示的语句,是否是另一串使用哥德尔数来表示的语句的证明。[原注4]
把数学语句翻译成数,看起来像是有趣的技巧,它是哥德尔不完备定理的证明的关键。
它如此重要的原因在于,它让我们把任何关于证明、可证明性的问题转化为关于数的算数问题。因此,为了证明任何(可证明的)语句,我们可以仅仅使用数以及数的性质。

例如,考虑这个被我称为Unprovavle(y)的语句。这个语句是:“y是某个语句的哥德尔数,并且不存在一个数x使得x是那个语句的证明的哥德尔数”。
因此,unprovable(y)本质上在说“y所代表的语句”是不可证明的。但是,它除了是一个关于证明与语句的问题以外,它还完全是一个关于数、数的算数关系的问题。
这个准确的算术关系是非常复杂的,不过的确可以被精确地定义。类似的,Prime(y),这个简单得多的语句语句“y是一个素数”, 存在一个算术关系Unprovable(y)。于是,Prime(y)断言了一个数如何,这个断言可以被一些相对而言比较简单的算术来判定。
现在,我们将来来带长途征程的最后一部分了。

哥德尔的证明的本源的想法是这句话:“这句话是不可证明的”。使用Unprovable(y)这句精确的数学语句,我们可以让这句不精确的语句完全精确。[原注5]
为了得到“这句话是不可证明的”的精确版本,我们将使用 “对角线引理”。(一条引理只是你用于证明其它定理的定理[原注6])。对角线引理表明了,就我们正在使用的数学系统而言,存在一个语句S它满足:S是真的,当且仅当Unprovable(G(S))是真的。(注意,unprovable(y)的输入是某个语句的哥德尔数。这个例子中,这个语句即S)
清楚一点说,对角线引理并没有证明S或者Unprovable(G(S))是真的,仅仅证明了它们或者同时为真或者同时为假。你开动脑筋,想想这到底啥意思?

对角线引理也表明了:一个未知的可能非常长的数学语句S,是真的,当且仅当 unprovable(G(S))是真的。但是unprovable(G(S))是真的,(根据unprovable(y)的定义)意味着S是不可证明的。
所以,如果我们能够证明“ 语句S是真的”,对角线引理表明我也能证明“unprovable(G(S))是真的”。但是,unprobable(G(S))说的是“S是不可证明的”!因此,S既是可证明的又是不可证明的,这就是一个矛盾。
因此,S必然是不可证明的。
语句S就是我们正在寻找的 “这句话是不可证明的” 这个语句的准确的版本。因此,不是每一个语句都是可以证明的。
可怜的数学,被人玩坏的数学……

[原注1] 关于数学系统,还有很多更加技术性的假定,比如,它必须是“有效的”,又叫做“可递归地枚举的”。对哥德尔的证明来说,这些假定是至关重要的。就我想向外行读者做介绍的这篇文章的主要部分来说,我觉得它们过于技术化了。我会在后面的脚注里面解释为什么那个系统需要是有效的。
[原注2] 算术的公理化也就是皮亚诺算术。皮亚诺并没有直白地提及所有的自然数。事实上,它仅提及了0.它拥有一个能否计算下一个数的“后继函数”S。因此,S(0)就是1的定义,S(S(0))是2的定义。所以,当把数学语句翻译成哥德尔数的时候,我们的编码仅需要给0、S赋值,而不需要给每一个数单独赋值。那意味着我们的编码仅需要考虑有限多个符号。
[原注3]这里指任何从我们的公理、选定的符号所生起的数学。
[原注4] 在上一篇文章中,我们忽略了很多重要的技术性的假设。其中之一,在这里说一下。那就是,你的数学系统(公理的集合)是有效的(effective)。在本质上,这意味着,存在一个这样的计算机程序:从理论上,能够列出你的数学系统的所有定理,而不列出任何不是定理的语句。对于不完备定理所考察的基本的数学系统——皮亚诺算术, 这一点是真的。对于标准集合论(ZFC),这一点也是真的。还存在一些不有效的系统,它们趋向于无用或无趣。比如有一个这样的系统:把算术中所有真的语句都作为公理。于是,任何真的东西都是公理,从而证明上是平凡的。为了让算术证明的校验(check)能工作,你的数学系统是有效的,这个假定是至关重要的。
[原注5] 哥德尔找到了一个直接说这个语句的方法。我们会采取一个略微不同的、更容易理解的途径, 不过哥德尔证明的主要动机是一样的。
[原注6] 引理一般是相对容易证明的,对角线引理也是这样。然后,它的证明是技术性的,并不是很有启发性。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa