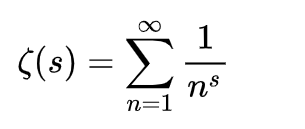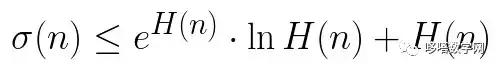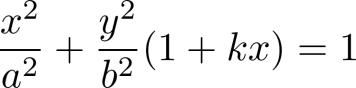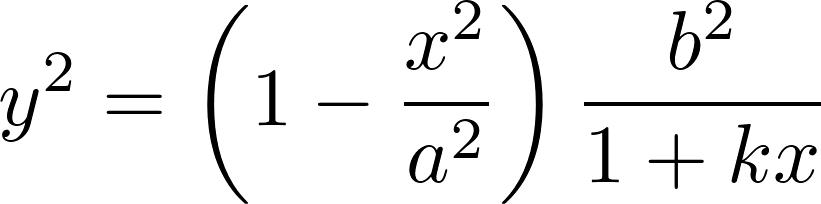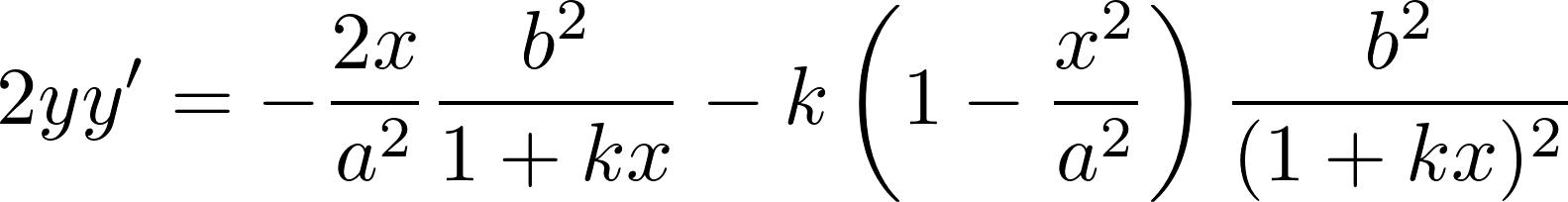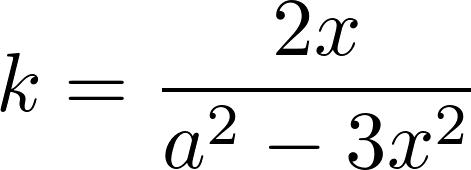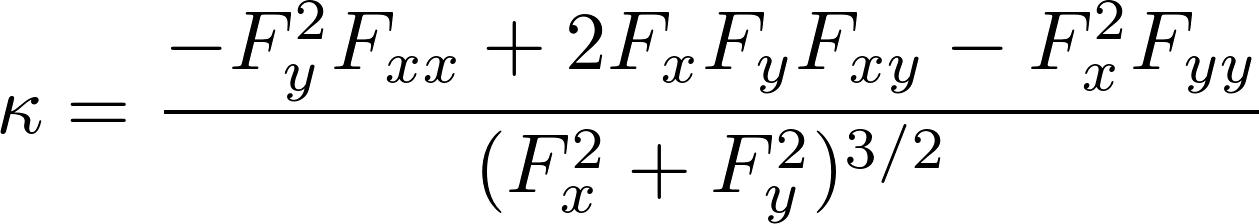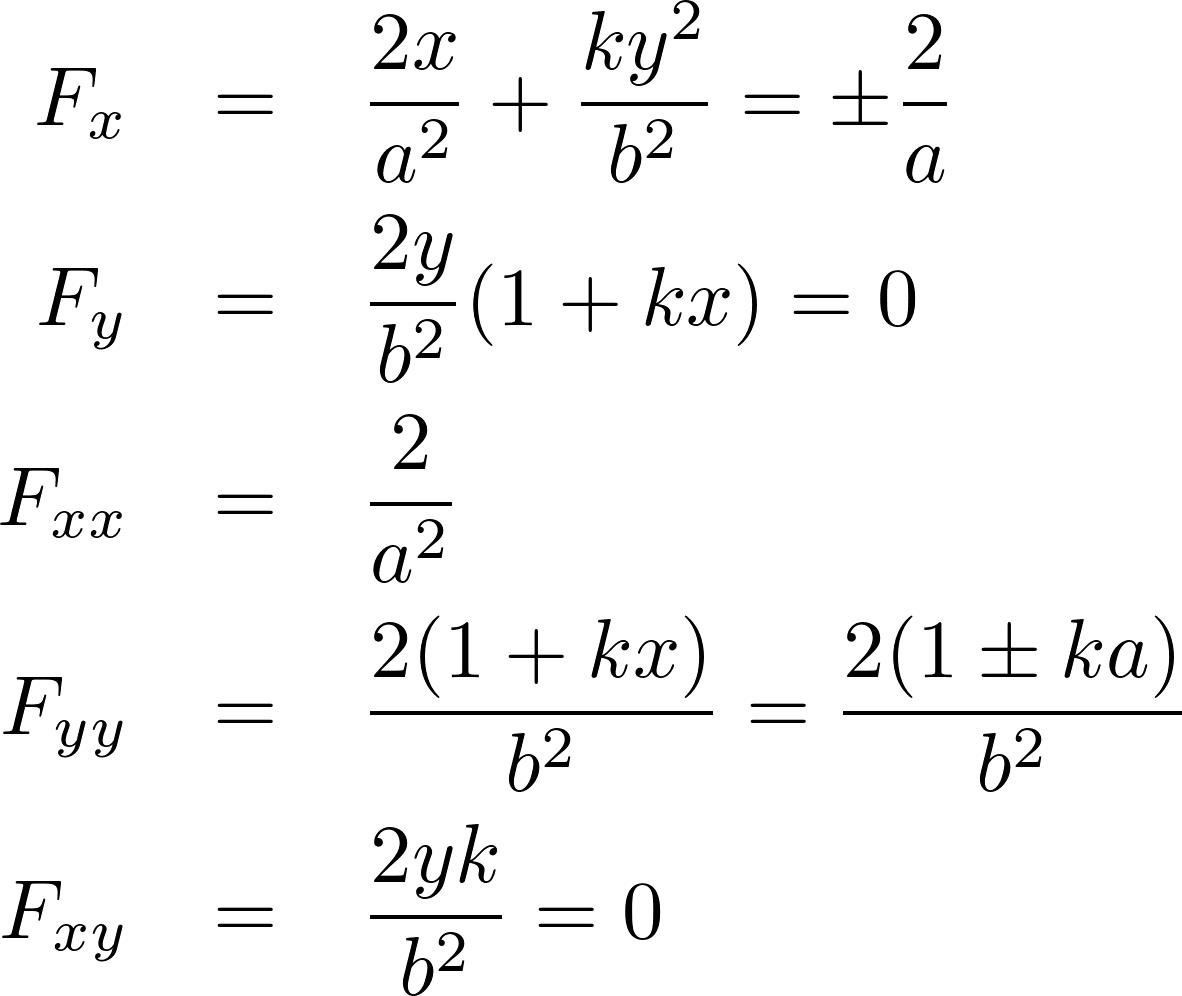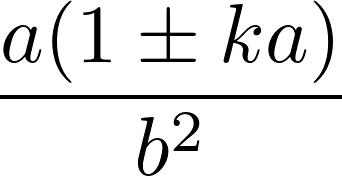关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

终于，在中秋节，我们一起看了阿蒂亚关于世纪大猜想黎曼猜想的证明发布演讲。这个演讲更像是一个宣称“我证明了”声明的又一次发布会，细节仍然不明朗。

不得不说，从发布会的角度来说，这是一次非常成功的“产品发布会”。人们在发布会前兴致勃勃的讨论，等待那一天的到来，直到“发布会”开始时，各路“粉丝”挤爆了海德堡获奖者论坛的官网，直播频道瞬间崩溃。论坛的工作人员不得不手举着自己的手机，来一场类似“抖音”式的山寨直播，让人心疼。

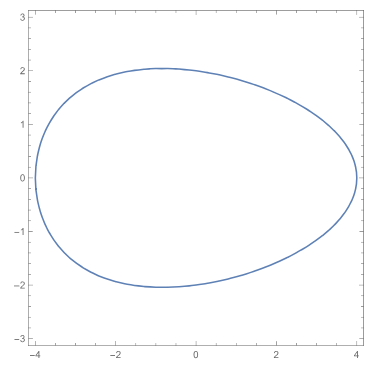
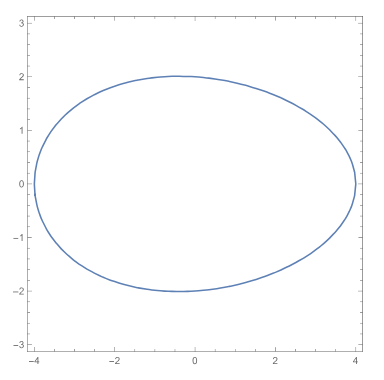
证明过程的最粗的主干，每个高中生都能理解。用的反证法，假设黎曼猜想不成立，在临界带中找一个不在临界线上的零点b，然后利用他那神奇的Todd函数T(s)构造新的一个函数F(s)。得到F(2s)=2F(s)，推出F是常值零函数。从而黎曼ζ函数是零函数，矛盾。

这个思路和宣讲开始前网上就披露的PDF论文一模一样，不过有的细节不同。比如论文中引出的矛盾点是F(s)=2F(s)，而不是上一段的F(2s)=2F(s)，我们暂且理解成笔误。关键是那个Todd函数具体是什么，仍然不明就里——即便网上有篇据说是阿蒂亚写的关于Todd函数的论文，里面的Todd函数的定义依旧不明确——至少从数学意义上来说是不明确的，它依赖于某个物理常数。

更有网友指出，阿蒂亚的这篇论证，引用了一个他自己的错误结论。而这个错误，在他一次学术演讲中，台下的听众当场指出了。

看来，这个是否是真的有一个惊天进展，只能继续等待了。

阿蒂亚结束演讲的时候，掌声是热烈的。但在数学里，再热烈的掌声都不及专家们苛刻的审稿意见来的权威。数学里，这些专家的从来都是挑剔的，无论你之前有多少成就，论文内容就是承认你工作的唯一指标。数学里，更为残酷的是，哪怕你有500页的论文，只需要一行的错误就可以否定你的全部。

未来的时间里，人们也许会催促、等待这个证明的更多细节，甚至，讨论班、答辩会纷至沓来，直到该领域的主要专家承认或者否定这个证明。——这是最好的发展轨迹，也有可能，作者永远不公布细节、不解释，从而石沉大海。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

近日，京都大学数理解析研究所(RIMS)贴出一篇10页的简短文章《为什么abc依旧是猜想》(Why abc is still a conjecture)，现在文章能在京都大学数理解析研究所(RIMS)上找到(http://www.kurims.kyoto-u.ac.jp/~motizuki/SS2018-08.pdf)阐述了望月新一教授提供的ABC猜想的论文并不能证明ABC猜想(there is no proof)。文章由两人合写，一位作者是)2018年菲尔兹奖得主彼得·舒尔茨(Peter Scholze)，另外一位作者是雅各布·斯蒂克斯(Jakob Stix)也是相关领域的顶级专家。

作者在文章开篇就明确指出，文章的论证有问题，而且认为通过小修小补并不能挽救整个证明过程。 文章指出的错误是关于关键的不等式（1.5）的证明。证明中关于j²系数的取舍有不可绕过的坎。当然，出于数学家的谨慎(或者是出于礼貌)，文章中两次提到是个人观点(in our opinion)。

abc猜想是一个数论猜想，最先由乔瑟夫·奥斯达利及大卫·马瑟在1985年提出。数论中，很多问题，包括一些菲尔兹奖级别的问题，都仅仅是abc猜想的简单推论。如果abc猜想能被证明，将是数论这门学科的重大进步。

2012年8月，日本京都大学数学家望月新一在其个人主页公布了有关abc猜想的“证明过程”。长达500页的证明，用到很多他自创的概念和理论。文章艰深，让众多专家也无法理解。但望月新一也没像其他学者一样，在各地举办讨论班解释他的论文，而是希望其他人自行阅读，从论文挖出更多有价值的东西——历史上格罗滕迪克的理论也有相似路径。于是，论文的正确性一直没有得到确认，一些人相信望月新一是正确的，但一些专家再没有确认之前，也表示不能认同。望月新一也撰文抱怨，数学界轻视了他的文章。于是，坊间开始流传“顶级论文无人能懂”的传说。

这回，指出其错误的舒尔茨教授，是数学界最顶级专家之一。作为顶级专家，不仅读了论文，还指出了错误。文章中也提到，望月新一试图解释他们提出的问题不是问题。结果如何，还得再看！

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

菲尔兹奖和阿贝尔奖双料得主阿蒂亚爵士（Sir Atiyah）日前声明证明了久负盛名的黎曼猜想。并将在9月24日在海德堡获奖者论坛上发表这个演讲。从目前论坛官网披露的信息来看，证明方法是一个全新的方法，但并不复杂(simple proof)。这次的证明基于之前冯诺依曼、希策布鲁赫、狄拉克的工作。

黎曼猜想是数学界最重要的猜想之一(有人说可以把“之一”两字去掉)。克雷数学研究所现在还悬赏100万美元征解。问题本身，只需要有过复变函数学习经历的人都能看懂。而它的一个等价变形，高中生都能看懂。

黎曼猜想原始版本

考虑下面一个函数项级数定义复变函数，

在实部Re(s)>1时，级数收敛，其余部分(s≠1)可以用解析延拓得到。解析延拓后的函数，叫做黎曼ζ函数。经过，一些简单的计算，对于负偶数，ζ(-2n)=0，那么负偶数就是黎曼ζ函数的平凡零点。而黎曼ζ函数还有别的零点，叫做非平凡零点。目前，发现的黎曼ζ函数的非平凡零点是的实部都是1/2。于是，黎曼猜想是说黎曼ζ函数的所有非平凡零点的实部都是1/2 。

高中生能看懂的版本

我们先来定义这样两个函数。

对于一个正整数n，我们把它所有的约数加起来，得到的正整数记为σ(n)。比如24的约数为1,2,3,4,6,8,12,24，那么σ(24) = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60。 

同样是正整数n，我们把不大于它的所有正整数的倒数加起来，记为H(n), 就是说H(n)=1 + 1/2 + 1/3 + ... + 1/n . 比如H(3)= 1 + 1/2 + 1/3 = 11/6 。 

通过σ(n)和H(n)，黎曼猜想等价于下面这个不等式成立：

是否是“真”证明还得等待

不过，声明要得到确认，需要同行专家审稿通过。数学界内，之前也有声明证明某个大猜想，最后发现证明错误的情况。就阿蒂亚爵士本人，之前也有“劣迹”，2016年他声明证明了六维球面S6上无复结构但没有了后文。

至于这次是真是假，作为吃瓜群众只能等待了。我们哆嗒数学网小编发稿时，海德堡获奖者论坛已经崩溃。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者：John D Cook。

翻译作者，独行者，哆嗒数学网翻译组成员。

校对，Math001。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

你将如何用公式描述一个蛋的形状呢？这里告诉你蛋的一个方程如下：

我们会发现，如果k=0，我们便会得到一个椭圆。k越大，越不对称于y轴。

我们在Mathematica上验证一遍：

代码

    ContourPlot[
        x^2/16 + y^2 (1 + 0.1 x)/4 == 1, 
        {x, -4, 4}, {y, -3, 3}
    ]

我们让k=0.05，这样看上去更像是一个椭圆。

对参数的研究

如果要对一个鸡蛋进行详尽的描述，你该如何确定a, b, k的值呢？

令y=0，则2a是鸡蛋的长度。令x=0，则2b是鸡蛋在中心的宽度。需要注意的是，这不是鸡蛋的最高位置，因为最高处在中心的左侧。（如果k是正数，则在左边。k可以为负数，这样最高处则会翻转到y轴的右边）。

我们通过确定最高处x的值来表示k。

我们有以下方程

隐函数求导可知

在最高处y的导数为0， 所以等式右边也应该为0。于是我们便知道了k的值。

曲率

k值越大，鸡蛋便会在左边变的越平整，右边则会越尖。我们会对鸡蛋两端的变化进行量化分析。

由隐函数F(x,y)=0确定的曲线，曲率可以由以下式子算出

上面的等式在我们关注的(±a, 0)两个点上可以化简掉很多参数。

于是，曲率简化成：

因此，在我们一开始给出的例子当中，当a=4，b=2和k=0.1时，左边的曲率为0.6，右侧的曲率为1.4。第二个例子，k=0.05，则左侧曲率为0.8，右侧曲率为1.2。

同样是这两个例子，那么如何计算鸡蛋的体积呢？

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa