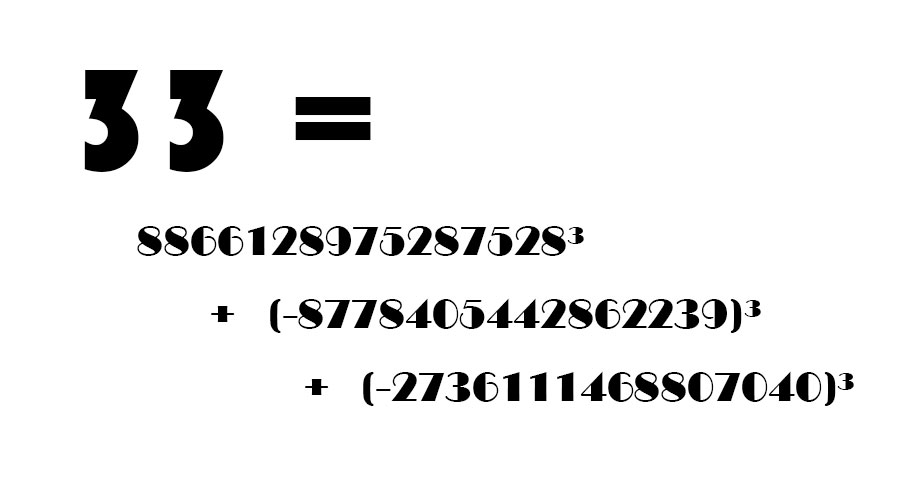作者,数学西瓜,哆嗒数学网群友。
校对,Math001
关注 哆嗒数学网 每天获得更多数学趣文
公元2019年3月的一天,一位叫Tim Browning(与Timothy Browning是同一人)的数学家再其个人主页上更新了一个网页,网页上的内容非常简单,没有任何多余的东西:
33 = 8866128975287528³ + (-8778405442862239)³ + (-2736111468807040)³
上面的算式是将自然数33用整数的立方和表示了出来。但是,可能出乎你预料的是,这是人类第一次知道,世间还存在着这样一个等式,第一次——我们第一次把33用这种方式写了出来!
为什么我们对这样一个等式如此着迷,让我们一起看下去。
建造房子式的“堆垒数论”
我们知道我们茅草堆垒出来能建造茅屋、砖石堆垒起来能建造砖房、钢筋混凝土堆垒起来能建造高楼大厦。
现在许多高楼大厦都是钢筋混凝土建筑的,但是是不是所有的高楼大厦都可以由钢筋混凝土来建筑呢?
这其实就是“堆垒数论”的思想。我们用简单的语言表达这个堆垒数论考虑的问题,如果考虑A、B两个整数的子集。如果A中的数都能被B中的某几个数相加得到,我们就说A能被B堆垒出来。大多时候,我们还要限制使用B中数字个数的数量。这时候,所使用的B中的数叫做堆垒项。
举几个例子:
如果A是所有不小于6的偶数集合,B是素数集合,并限制只能用2个B中的数。那么问题就是著名的哥德巴赫猜想。
如果A是自然数集合,B所有完全平方数集合,并限制只能用2个B中的数。自然数的能不能写成两个数平方和问题。
如果A是自然数集合,B所有完全平方数集合,并限制只能用3个B中的数。自然数能不能写成三个数平方和问题。
以此类推……
有时候,我们还可以反过来研究,比如,如果所有自然数都能被B中的数加出来,那么多少个数之内一定能办到?
我们用233来举例子把:
下面这些正整数方程是否有解呢:
233 = x² + y²
233 = x² + y² + z²
233 = x² + y² + z² + w²
233 = x² + y² + z² + u² + v²
以上方程中的所有未知数地位是一样的,我们把那种通过交换顺序能变得一样的解看成相同的解可以得到:
第一个方程,有一组解:
233 = 8² + 13²
第二个方程,有两组解:
233 = 1² + 6² + 14²
第三个方程,有三组解:
233 = 2² + 6² + 7² +12²
233 = 3² + 4² + 8² +12²
233 = 4² + 6² + 9² +10²
第四个方程,有一组解
233 = 2² + 4² + 7² +8² +10²
在第三个方程的正整数解中,我们可以看出可以出现一样的元素12;
关于第四个方程有一则小故事,根据迪克逊的《数论史》(History of the Theory of Numbers)记载。1867年,史密斯(H. J. S. Smith)开始推广表为5个,7个平方数的结果。一位不为人知的委员会成员曾向巴黎科学院建议举办1882年的数学科学大奖(grand prix des science mathématiques)赛题目为“表为5个平方数的方法数”。实际上1881年春天就发布了公告悬赏这个问题,后来才将其作为赛题。史密斯和闵可夫斯基(H. Minkowski)(值得注意的是,闵可夫斯基当时才18岁)都获得了该大赛的全额奖金。他们俩都发展了n元二次型理论来求出表为5个平方数的方法数。
迷人的平方和
上面第一个方程为费马双平方和定理(Fermat's two-square theorem)的一个特例。费马还是“一如既往地”只写命题不给证明,这个命题也一样。这个命题最早被欧拉证明的。费马的这一命题即给出了所有4n+1型的素数都可以唯一地分解为两个平方数之和(至于如何求其唯一表示可以参看西尔弗曼的《数论概论》第26章)。那么其他数呢?
有下面一个定理:
一个大于1的整数可以写成两个平方整数之和,当且仅当的它的标准素数分解中不包含4n+3型素数或者4n+3型素数是偶次。
比如637 = 7²·13有两个素因子7与13,而是4n+1型,而7模4n+3,但素数7的次数为偶数2,故637 可以表示为两个平方数之和。实际上,637 = 14²+21²。
关于平方,我们还有勒让德三平方和定理(Legendre's three-square theorem):
整数可以写成三个整数的平方和(即允许堆垒项为零),当且仅当的它不为4^a(8b+7)型的数。(其中,4^a表示4的a次方,a与b都取自然数)
值得注意的是这里用的是“三个整数的平方和”与双平方和情形的描述有所不同。
勒让德的这一定理可以写为等价形式:
整数可以写成少于四个平方数之和(默认平方数从1开始),当且仅当的它不为4^a(8b+7)型的数。(其中,4^a表示4的a次方,a与b都取自然数)
对于平方数且时,有拉格朗日四平方和定理(Lagrange's four-square theorem)
每一个自然数可以写成四个整数的平方和(即允许堆垒项为零)。
我们不应该去纠结于当需要表示的数比较小时(比如取5、6,堆垒项总有零出现),四个整数中会出现零。我们应该看到当需要表示的数为很大很大的整数时,都可以由四个平方数来表示,就像再厉害的野马(大整数)都可以被这位驯马师(拉格朗日四平方和定理)驯服,这便就是此定理的重要意义。
华林问题
什么是华林问题呢?
1770年,英国当时的领袖数学家华林(Waring)(别因为音译名将其当作华人)在其《代数沉思录》(Meditationes Algebraicae)第二版中提到一句话:
每一个正整数可以写成4个整数的平方和(即允许堆垒项为零);可以写成9个正整数的立方和,可以写成19个整数的四次方和,如此等等。
当然这句话的一部分就是拉格朗日的定理,第二部分是华林通过大量数值试验得出的猜想,第三部分也是他得出的猜想。
对于每一个给定的正整数k,存在一个最小的正整数g(k),使得每一个自然数都可以写成不超过g(k)个整数的k次方和。
其中求g(k)的问题便是华林问题。经过上面关于平方数的介绍,我们知道了g(2) = 4。
1909年,德国数学家韦伊费列治(Wieferich)证明了g(3) = 9;后发现漏洞,于1912年由生于英国的美国数学家肯普纳(Kempner)补正;
1940年,印度数学家皮莱(Pillai)证明了g(6) = 73;
1964年,我国数学家陈景润证明了g(5) = 37;
1986年,三位数学巴拉苏布拉玛尼安(Ramachandran Balasubramanian)、德雷斯(F. Dress)和德西霍勒(Deshouillers)证明了g(4)=19;
再回来,整数立方和还有42
好了,回到我们最初的问题:自然数的整数立方和表示。在k=3时的华林问题中,我们知道每一个正整数都可以为不超过9个正整数的立方和;
如果将前面华林问题的堆垒项只允许用加法的条件放开,我们允许用减法,是什么情况呢?——这个问题其实就是简易华林问题——不要因为其命名为“简易华林问题”就觉得其比“华林问题”简单。
而将正整数表示成三个整数立方和的问题,就是堆垒项限制为3的简易问题。现在这个问题依然是没有解决的问题。
我们用v(k)表示满足相应条件最小的正整数,即对应于华林问题中的g(k).
1932年,V. Vesely证明了v(k)存在。
接着赖特(E. M. Wright)于1934年得到一个粗糙的估计:(此估计不等式的证明可以参看陈景润写的《初等数论Ⅲ》132页的内容)
v(k)≤2^(k+1) + k!/2
不久,赖特又对其改进,符号比较专业就不详述了。
再后来赖特还得到了v(k)≤2^(k+1) +4k,并研究了具体值。
1936年,莫德尔(Mordell)证明了除极少一部分数不能确定外,大部分整都适合v(3) = 4.
我国数学家柯召曾列出一张表,将100以内的数分解为4个立方数之和,表中几乎每一个数均可分解为x³+y³+2z³的形式,仅有两个例外
76 = 10³+7³+4³-11³,
99 = 5³+3³-1³
柯召教授这样做的目的或许是为了说明v(3)=4是正确的,但是这仅仅只能作为一些数值试验。
2003年,科学出版社出版了中文版的《数论中未解决的问题(第二版)》。其作者是为盖伊(1916年9月30日~)现在已经102岁高龄了。
在《数论中未解决的问题(第二版)》的第D章(该书编写了A~F章节)的D5问题中,提到除了形如9n±4数尚且不知道结论,对于所有其他的数都证明了是4个整数的立方和。
了解同余的小伙伴们,可以做下计算,任何整数的立方在mod 9 的情况下只有-1,0,1三种可能。所以 x³ + y³ + z³ 在mod 9 的情况下,只有0,±1,±2,±3这7种可能,而±4是不可能的。
所以形如9n±4数一定不能表示为三个整数的立方和。由此我们也可以知道v(3)>3,也就是说所有自然数不能仅由三个整数的立方和表示。但是退而求其次,哪些数可以由三个立方数表示呢?数学家们希望有像“费马双平方和定理”、“勒让德三平方和定理”这样的定理来引导人们,但是目前为止还没有。
接下来我们要步入主题了!
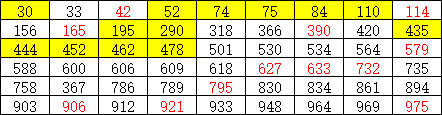
所有不为9n±4型的数都是三个整数的立方和吗?盖伊书中写道:1992年,他对所有小于1000的数用计算机搜索后发现,除了下面(标红部分截止2019年3月都还没有被解决)表中的数以外,对于其他小于1000的数都找到了这样的表示。
在1993年5月25日的一封电子邮件中,Andrew Bremner告诉盖伊有:
75 = 435203083³+(-435203231)³+4381159³
Conn和Vaserstein发现了
84 = 41639611³+(-41531726)³+(-8241191)³
后来人们找到了(上表标黄部分)
30=(-283059965)³+(-2218888517)³+2220422932³
52=60702901317³+23961292454³+(-61922712865)³
110=109938919³+16540290030³+(-16540291649)³
195=(-2238006277)³+(-5087472163)³+5227922915³
290=426417007³+2070897315³+(-2076906362)³
435=4460467³+(-4078175)³+(-2755337)³
444=3460795³+14820289³+(-14882930)³
452=(-2267462975)³+(-3041790413)³+3414300774³
462=1933609³+(-1832411)³+(-1024946)³
478=(-1368722)³+(-13434503)³+13439237³
2007年,Michael Beck, Eric Pine,Wayne Tarrant与Kim Yarbrough Jensen这四位数学家的论文指出小于1000的数还没有找到解的剩下:
33, 42, 74, 114, 156, 165, 318, 366, 390, 420, 543, 579, 609, 627, 633, 732, 758, 786, 789, 795, 903, 906 ,921, 948, 975
2016年,Sander G. Huisman指出小于1000的数还没有找到解的就剩:
33, 42, 114, 165, 390, 579, 627, 633, 732, 795, 906, 921, 975
最近,由Booker Andrew提交了一篇论文"Cracking the problem with 33",论文中找到33这个文章开头的结果,由Browning公之于众。我们可以看到每个元素都是10的16次方的数量级,要读出来应该快读到亿亿位了!
另外在数学节目Numberphile中,Timothy Browning做了一期名为“The Uncracked Problem with 33”的问题介绍,可惜目前没有中文字幕。可以从论文"Cracking the problem with 33"的摘要与论文标题看出Andrew Booker写这篇论文正是源于该视频。
也就是说到目前为止,100以内的自然数就剩下42还没有找到关于立方和的整数解了!
关注 哆嗒数学网 每天获得更多数学趣文