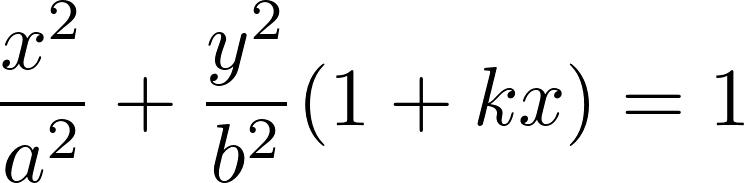原文来源于罗巴切夫斯基大学。
翻译作者,radium,哆嗒数学网翻译组成员。
校对:donkeycn
关注 哆嗒数学网 每天获得更多数学趣文
2018年6月29日 于,罗巴切夫斯基大学
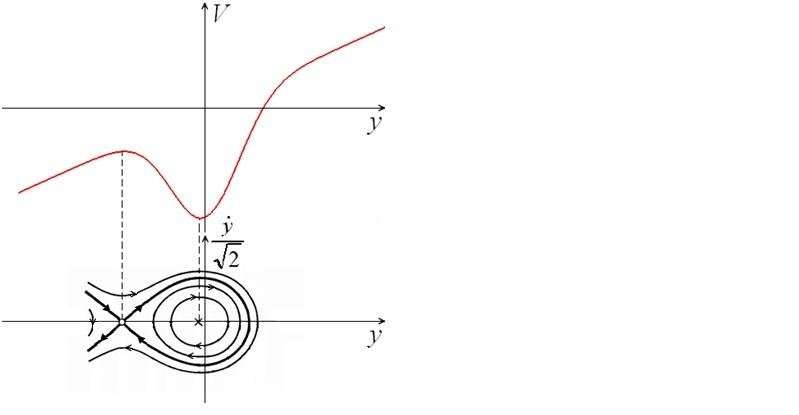
(图注:在没有外部干扰的情况下社会系统发生冲突的相轨线)
洛巴乔夫斯基大学国际关系和世界历史研究所副教授亚历山大·佩图霍夫领导的一个研究团队,在非线性动力学的基础下对社会冲突模型进行了优化。
对于数学建模而言,社会和政治进程的一个重要特征是它们无法被严格定义。它们通常受到一点微小的改变和波动的影响。通常,社会进程被看作布朗粒子。粒子轨迹中的一点微小的改变和波动可以解释为其他粒子的混沌运动。在社会进程中,波动可以视为是个体自由意志作用的表现,以及一些外部环境带来的随机影响。
在物理中,这些过程通常用朗之万随机扩散方程( Langevin's stochastic diffusion equation)来描述,这一方程也已经被用于模拟一些特定的社会进程。
基于这一方程建立的模型有以下优点:
1、如同前面提到的一样,该模型允许人们考虑个体自由意志作用下的的影响与系统外部环境产生的影响。
2、社会系统的行为可以从整体和个体两方面来计算。
3、在这个模型中,可以根据不同的初始条件识别社会系统运转的一些特定的稳定模式。
4、扩散方程作为数学工具,完全可以通过数值模拟进行验证。
这个模型基于这样的想法:社会中的个体通过一个通信场(communication field)来实现互动。这个由社会中的每一个体所产生的场就用来模拟个体间信息的交流。
但是,可以想到,这样的社会很难归因于经典物理拓扑空间中的对象。
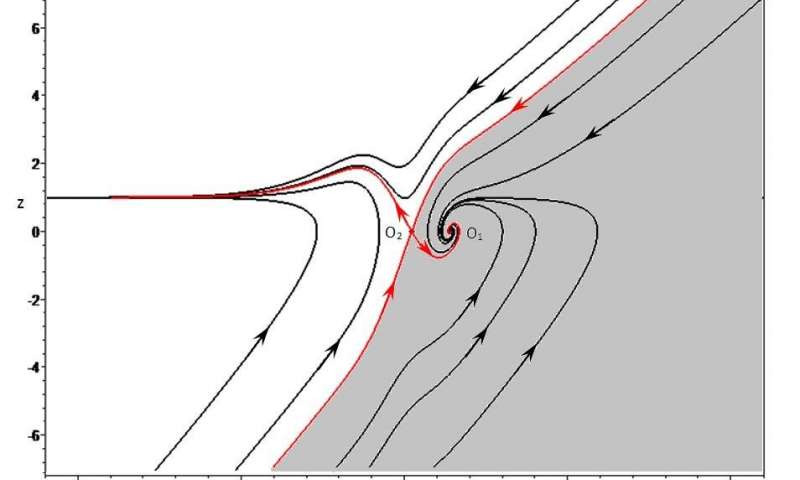
(图注:在外部干扰的情况下社会系统发生冲突时的相轨线)
佩图霍夫(Dr. Petukhov)博士认为,从个体之间信息传递的角度来看,社会空间将经典的空间坐标与一些附加的具体特征结合了起来。这一点可以通过以下事实来解释:在现代信息世界中,我们没必要非得靠近一个对象才能向他传递信息。
亚历山大·佩图霍夫指出:“因此,社会是一个多维的、群居以及物理性的空间。它反映了一个人用他的通信场“接触”另一个人的能力,即影响那个人、他的参数和在特定空间中移动的能力。”
因此,在这个空间中,个体相对于其他个体的位置刻画了他们之间的关系水平和参与信息交换的能力。
在这个模型中,当两个个体的位置靠得很近时意味着它们之间有规律的信息交换,这样便可以建立相应的社会联系。
在这样的背景下,如果个体或群体之间信息传递的变化导致了距离上的急剧增加。(即社会距离Δx = xi—xj,这里x表示社会和物理空间中的坐标,i,j=1,…,N,其中N 为个体或者群体的数量”)那么,它们之间可以认为是一种冲突。
因此,在假设中,个体可看作是布朗粒子并以一定的半径范围对其他个体产生影响。这样的通信场可以用扩散方程来表示。
基于上述方法,洛巴乔夫斯基大学研究人员研发的模型,揭示了以下特征模式和对初始和边界条件的依赖性:
1、考虑外部的影响和控制的条件下,例如出现社会冲突并且加剧的背景下,建立了特定的边界条件,这样的条件是由社会系统参数决定的。
2、建立了一个有关社会系统稳定性的特有区域。在这个由相轨线确定的区域中,所研究的对象之间保持了相对较小的社会距离。这就是群体积极互动,并保持连续信息交换的特点。同时,还可以观察到该区域是怎么变化的,这取决于冲突管理函数的影响。
3、通过引入的控制函数的参数确定并联系这些边界状态,可以反映当代特定种族-社会冲突的模式。因此,该模型可以作为预测不断变化的冲突和得出冲突解决方案的工具。
这也证明了在这些研究过程中,一个分布式多元认知系统从一个稳定状态到不稳定的状态受阈值的影响。
根据亚历山大·佩图霍夫的说法,洛巴乔夫斯基大学的研究人员进行的相关实验已经揭示了控制这种系统所需的具体参数:它们决定了系统从稳定状态到不稳定状态的转变,这使得完全通过控制这些参数去创造或阻止社会冲突成为可能。
亚历山大·佩图霍夫说:“通过继续研究这个方法,我们将能够在其基础上创造一个足够有效的预测社会冲突的工具。”
关注 哆嗒数学网 每天获得更多数学趣文