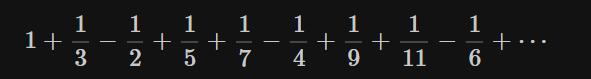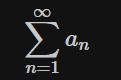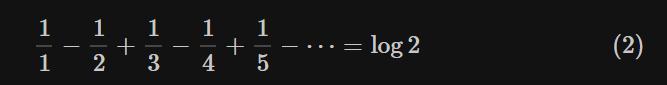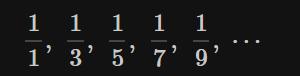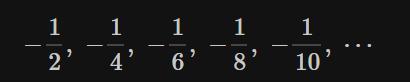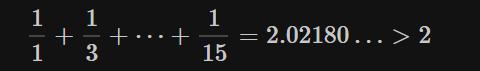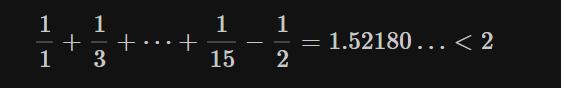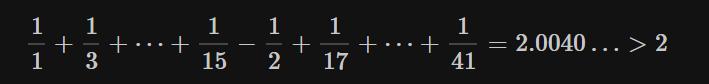什么是空间?
作者:Marianne Freiberger,+Plus 记者
翻译,清风掠旷野,哆嗒数学网翻译组成员。
关注 哆嗒数学网 每天获得更多数学趣文
在最近一次的“科幻、科学”活动的投票中,有人想要了解这个问题,于是我们邀请了Francesca Vidotto和George Ellis来为大家解答这些问题。
空间就是你站在的地方
空间就是一个舞台,物理的大戏不断在其中上演。如果你手上正好有一部手机,你可以很容易地借助手机内置的GPS装置确定你在空间中的位置,当然,是以地球的位置作为参考的坐标。当你开始移动的时候,对应的坐标的变化就刻画出了你的行动轨迹。空间和身处空间这个舞台中的物体无关。它不在乎你,或者其他任何在它之中的物体如何变化。即使所有的物体都消失,空间仍然存在。

以上是我们在学校学习到的空间的样子——一个刚性的盒子,万事万物都被包含在这个盒子里——并且,很难想像除此之外还有其他的空间的样子。这个观点在牛顿1687年出版《自然哲学的数学原理》之后占据了主导地位。牛顿在书中写道:绝对的、真实的、数学上的空间始终保持着一种不变和静止的状态,它与一切外在事物无关。
牛顿没有宣称他能够证明物理上的空间真的如上所述。“他意识到,他的陈述只是一个假说”,荷兰奈梅亨大学的理论物理学家Francesca Vidotto这样说,“但这个假说是这样强大,以至于我们可以据此建造桥梁,甚至探索外太空。”牛顿关于空间的假说如此强大,它强大到足以覆盖几个世纪以来关于这种抽象的、独立于物理实体之外的虚空是否真的存在的哲学争论的价值。
GPS卫星。如果它与地球,以及其他所有的一切都消失,空间还存在吗?(图片由NASA提供)

手指之间的空间
有一套数学体系牛顿的假设发展而来的,它是建造桥梁、制造飞船的基础知识。它基于一个和我们的直觉相符合的认识:空间是连续的。理论上,我们可以将空间任意放大,并且不会出现它分解为一块块最小像素之类的情况。
从另一个角度看,连续性是很让人难以置信的。一段连续的线,无论有多短,总是由无限多的单独的点组成。由于有太多的点,以至于无法用像 1,2,3,… 这样的整数给它们标号。如果有足够的时间,我们总可以给排队等候的人标记序号,即使是一条无限长的队。但是连续的线的情况与无限长的队列完全不同。连续的线给出的是不可数无限,它比无限多个的离散的点要大得多得多。所以,如果假设空间是连续的,就意味着要承认你手掌那么大小的空间中包含着一个可怕的无限。
“把你的手指分开10厘米”,南非开普敦大学的宇宙学家和数学家George Ellis解释道,“如果你相信你两跟手指之间有一条由点构成的连续的线,那就意味着你相信,在你的两根手指之间存在不可数无限多的点。那是完全不合理的。我认为那只能是一个数学上的想法,而不应该在现实世界中成立。”
空间扭曲
Ellis可能是正确的。对牛顿“绝对时空”的第一次冲击来自20世纪初爱因斯坦提出的相对论。相对论将空间的地位从舞台变为了舞台上的演员。爱因斯坦意识到观测者通过空间的方式会对时间和距离的测量产生影响。所以,时间和空间就被联系起来,称为“时空”。他还意识到时空能够被弯曲。在此之前,人们认为重力是一种超距作用。但是,爱因斯坦指出,重力只不过是时空几何学的产物。超大质量的物体,例如太阳,能够明显地弯曲时空,进而能够改变小质量物体经过它的轨迹。就像弹珠的滚动轨迹受到别的物体对它的碰撞以及它所在表面的曲率的影响。

当超大质量的物质集中到一个非常小的空间区域(当超大质量的恒星向自身内部坍缩时候才会发生),时空变得非常弯曲,以至于形成了黑洞。黑洞对物质的引力非常非常地大,同时时空的弯曲程度又非常高,以至于没有任何物质可以从它周围逃逸,哪怕光也不能。这意味着外界无法看到黑洞内部的样子。我们也无法进入黑洞而后再出来,向周围人讲述所见所闻。不论黑洞之中发生什么,外界都无从得知。
粒子和波
20世纪早期物理学的另一个重大发现是量子力学。量子力学描述构成物质的最微小粒子的行为。它的基础是一种违反人类直觉的概念——微小粒子(例如电子)的行为,有时像撞球,有时像波,它们同时具有粒子和波的特性。基于这一概念的最著名的结果是海森堡不确定性原理。假设有一个粒子,我们想要研究它的位置和动量(动量=质量×速度)。不确定性原理表明,如果我们测量的位置越精确,那么相应的动量的误差就越大,反之亦然。如果动量测量越精确,那么位置测量的不确定性就会增加。这不是因为我们不知道粒子在哪里,而是它某种程度上同时出现在许多地方。用Δx表示位置的不确定性,用Δp表示动量的不确定性,海森堡不确定性原理可以表述如下:
Δx×Δp≥ h/(4π)
h = 6.60606957 × 10^(-34) m²kg/s
尽管如此,这个不等式仍然表明,位置和动量不能同时地任意小。
最小的长度尺度

当我们尝试将量子力学与相对论结合在一起时,就会有出乎意料的发现。想要观测空间某一区域,我们就必须至少向那个空间投放一个探测粒子(例如光子)作为探测手段,观测探测粒子对该空间内物质的散射情况。如果空间区域R足够小,小到它的直径只有Δx,根据海森堡不确定性原理,探测粒子动量的不确定性就会非常大。巨大的动量意味着巨大的能量,进而意味着很大的质量(根据爱因斯坦质能方程):
E = mc²
E表示能量,m表示质量,c表示光速。
因此,将一个粒子限制在狭小空间就意味着在这个空间集中了巨大的质量。如果空间R足够小,以至于低于某个临界值,这是探测粒子的质量将变得极其地大,足以形成黑洞,吞噬掉空间R以及所有在它内部的物质。临界长度称为普朗克长度,其 数量级为10^(-35) m。这一数值难以想象地小,但它远不是0。所以,根据这个思想实验,所有足够小的空间都把自己隐藏起来了,所以我们什么也看不到。
“这告诉我们,在普朗克尺度下讨论距离和长度是没有意义的。”Vidotto说道。但,那是否表明,我们无法看到任何比普朗克长度小的东西?抑或是不存在比普朗克长度小的东西?“在我看来,这是个最基本的问题”,Vodotto说,“你可以把发现普朗克长度以下的物质视为一项伟大的发现。”
所以,我们可以认为,空间是由许多普朗克长度尺寸的粒子组成的。我们再也无法把空间无限细分。“我认为,我们有理由相信,时空是由不可再分的粒子构成的,”Ellis说道,“把你的手指分开10 cm,中间确实有大量的实体粒子,但总不是无限的。”
让我们接受最小长度的理由来自将相对论与量子力学结合起来的朴素尝试。但这一朴素尝试很快陷入困境,因为它给出了矛盾的、荒谬的预测。物理学家目前还没有提出非常成熟的量子引力理论。目前有两个可能正确的理论——弦论和圈量子引力论。“这两个理论都表明存在这一基本尺度,”Vodotto说道,“但也有一些理论框架没有用到基本尺度这一概念。”
那么是否可以通过实验验证呢。“首先,你要知道,那是真的真的真的很小很小很小,”Vidotto解释道,“日常生活的尺度与质子大小尺度的差别,跟质子尺度与普朗克长度尺度的差别是一样大的。那是真的太太太太小了。”探测普朗克长度尺度的物理现象需要的能量超过了人类目前的科技所能达到的极限。
“我认为,假如有一天我们看到了时空不连续的痕迹,那应该是宇宙学领域的进展,”Vidotto说道,“这种不连续有可能在宇宙微波背景辐射(大爆炸辐射的残留)中留下了一些痕迹。从宇宙微波背景辐射中,我们能够提取到早期宇宙的部分信息。现今宇宙的结构,包括恒星、星系、星系群等等的形成都可以追溯到早期宇宙的状态。或许,未来的某一天,我们能够理解早期宇宙的状态是如何直接地导致了量子不连续的结果。”
还有一种可能性,来自宇宙遥远的另一端的观测能帮助到我们。按假设时空原子的结构可能会改变光速。通过观测从遥远宇宙深处传来的光,我们可以计算出时间的延迟。“现有技术可以保证这一观测的实施”,Vidotto说道,“几年前MAGIC天文望远镜就观测到了一次时间延迟。但是一次测量不足以得出坚实的结论,尤其是在我们还没有完全弄清楚它背后的物理过程的情况下。”
就算时空本质的粒子属性终有一天会被证实,这也不妨碍我们在日常生活中遵循牛顿的直觉。作为对世界本质的描述,牛顿物理只是近似正确。但这种程度的近似足够完美地解决我们日常生活的时空尺度下的所有问题。正如Vidotto指出的那样,“一个优秀的物理学家,总是能够根据适用场景选择适合的物理理论。”
评论1 : 本文指出,任何物质都无法逃脱黑洞的引力。但是,最近发表的论文证明,信息可以逃离黑洞。(这个好像在霍金的科普书上看到过一点点,题目是“黑洞并不是真的黑”)
2011年8月11日,约克大学两位科学家的新发现给出了关于黑洞物理本质的新观点。传统观点认为,黑洞是空间中质量超大、密度超大的物体,可以弯曲空间,它可以吞噬一切距离它太近的物质,没有什么东西可以逃出它的引力范围。但Samuel Braunstein教授和Manas Patra博士的发现表明,信息可以从黑洞逃离。这一暗示可能具有革命性的意义——引力可能不是最基本的力。Braunstein教授介绍道:“我们的研究不需要黑洞弯曲空间的几何细节。它借鉴了一项最近提出的想法——空间、时间,甚至是引力本身可能都是一个更深层次理论的引力熵力性质。我们的工作认为,量子信息论可能是引力的熵力理论的根源。”
评论1的补充:
“虽然不能声称证明了逃离黑洞的可能性,但那是这个研究结果最直接的解释。事实上,研究结果表明,量子信息论会是将量子力学与相对论结合起来的关键理论。”
关注 哆嗒数学网 每天获得更多数学趣文