本文编译自+Plus网站
原文作者:Marianne Freiberger 、 Rachel Thomas
编译作者:Math001
关注 哆嗒数学网 每天获得更多数学趣文
哆嗒数学网
这里是数学爱好者之间分享数学经验、数学心得的数学文化家园。欢迎一切对数学具有浓厚兴趣或疑问的人们。在这里,你不必担心成为绝望的孤岛独思者。这里有千千万万的同伴,陪你一同在数学海洋里畅游。
346篇原创内容
公众号
维娅佐夫斯卡(Maryna Viazovska)是2022年菲尔兹奖得主之一。菲尔兹奖每四年颁发一次,只颁发给40岁以下的数学家,被誉为数学界的最高荣誉之一。
维娅佐夫斯卡是史上第二位女性菲尔兹奖得主,她获奖的成果和我们日常生活中经常见到的一些事物有关。

从桔子开始
运水果的确不是一件轻松的事情。不仅水果会经常被挤变形,即使不考虑变形,把桔子考虑成最简单的球形,也会有问题。无论你怎么装箱,都会留下缝隙。这就自然的会提出一个几何问题:我们如何排布这些球状水果,能让水果尽量多的装到箱子里?比如怎么样装桔子,可以让桔子占箱子里的空间比率最大?
"假设有个巨大的箱子以及数量巨多的球体,"维娅佐夫斯卡说,"同时简化一下问题,球体是刚性的不能被挤压,另外每个球都是相同大小。我们要尽可能多的在箱子里放置这些球。"
如果盒子很小,那么答案可能和盒子的形状有关。但如果盒子很大,形状的影响可以忽略不计,答案只取决于盒子的体积。“这在直观上很显然,存在一个最大的可以用等大小球体填充的体积比,虽然在数学上需要做一些工作才能证明这一点。” 球体堆积问题就是找到这个最高比率,也称为球体堆积常数。

再来一个更简单的例子,让我们降低一个维度:我们不是将球体排布到3维空间中,而是将圆盘排布到2维空间中。“在2维空间中,最佳排布是蜂窝状排布,”维娅佐夫斯卡解释说。通常的蜂窝每个单元都是六边形,六边形整齐地组合在一起,彼此之间没有空间。如果您以相同的模式排布圆盘,您确实会出现间隙,我们能证明这的确是最密集的排布“这样,我们就用这些同样大小的圆盘覆盖了 90%多一点的面积 。”实际上二维球体堆积常数的精确值为
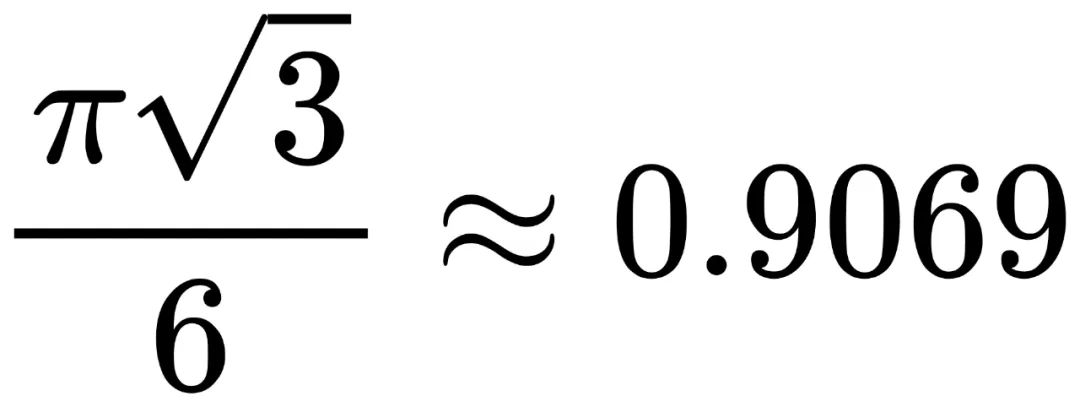
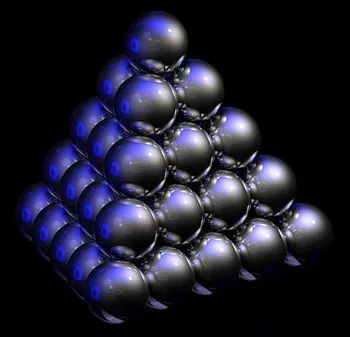
"三维空间的情形被称为开普勒猜想,已经400多年没有解决了,"维娅佐夫斯卡说,"三维空间里我们不止一个最佳堆积,我们有很多比率相等的最佳堆积。"其中一种你在菜市场也见过,就算把桔子摆成金字塔的形状(见上图,我们用球代替桔子)。这种方式的堆积密度大约是74%。实际上三维球体堆积常数的精确值为
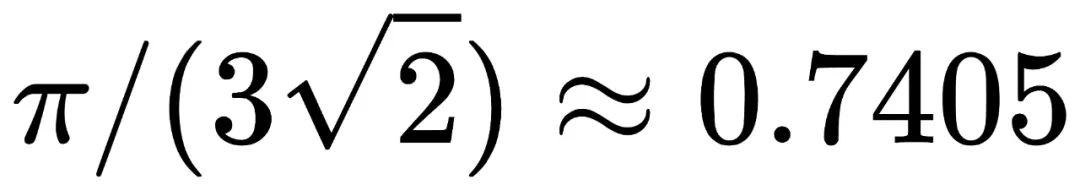
1998年有一位数学家给出了这种堆积是最佳堆积的证明。海尔斯(Thomas Hales)用250页的传统形式的数学论文,加上3GB的计算机代码和数据做计算试图证明它。这是富有争议的证明方式,因为没人能在有生之年去验证计算机产生的数据,所以海尔斯工作是否是完成了证明还没有最终确定。也有专家团队说有99%把握确认这套证明是对的,他们使用了计算机形式逻辑参与验证。
高纬度的球体堆积
不用计算机,只用几页纸,维娅佐夫斯卡给出了最牢靠的证明。这是在高维空间的球体堆积证明,即 8 维和 24 维空间。这样的工作似乎除了烧坏你的脑袋并没有什么别的用处,但事实并非如此。高维空间中的球体堆积在通讯技术中非常重要。它能确保我们通过互联网、卫星、电话传输信息的时候,传输过程有干扰的情况下,也能理解传过来的信息。
为了把控更高的维度,我们要从二维转向三维,我们把思绪再次回到中学阶段。如果你也是那种三维立体图形画图困难户,那你就要感谢代数的作用了。三维空间中的点由3个坐标值表示,线和平面等形状用相应的方程表示。如果你无法想象图形之间的关系,这些方程可以帮到你。
在高维空间中,也适用同样的原理。n维空间的点由n个坐标值表示。和2维以及3维空间一样,你可以给出高维空间中距离和体积的概念,然后定义包括高维球之类的各种形状,这些都是用方程来定义。虽然这些图形无法作图了,但是用代数方法可以处理它们。所以,你同样可以定义高维空间中球体堆积以及堆积密度的具体含义。
回到2维和3维的情形,我们来看看如何从2维的情况推广到3维:先用刚才2维上的蜂窝排布的方式把3维的球体在平面上铺一层,从2维角度看,这是最佳堆积。然后在这一层上铺第二层,第二层的球都铺在第一层的凹陷处。然后继续第三层、第四层……这样的确会产生一个最佳堆积,所以人们会想当然的认为,这种推广方式会自然的推广到高维情形。
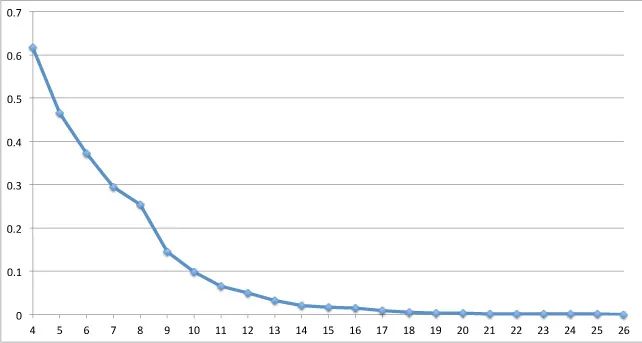
哎呀,但事与愿违。知道其中一个维度的最佳堆积和对推算下一个维度的最佳堆积并没什么用。下图展示了4维到26维目前人们知道的最佳的堆积的下界。从图上看,呈指数级下降趋势。
寻找上界
我们寻找的数是某种意义的最大值,比如说堆积密度的最大值。但是,往往没那么好的运气说找到就找到,这时候我们就要退而求其次,去找一个上界:一个数,那个还没求出的堆积常数一定不超过这个数。
不同维度的堆积常数上界陆续被人们提出。2003年科恩(Henry Cohn)和艾尔基斯(Noam Elkies)研究出了一个非常有趣的求上界的办法,可以用于任何维度的计算。但这个办法有实际操作上的难度,所以两个人也只把这些上界算到32维的情况。结果就是下图,包含4到28维的情况,绿色是下界,蓝色是上界。
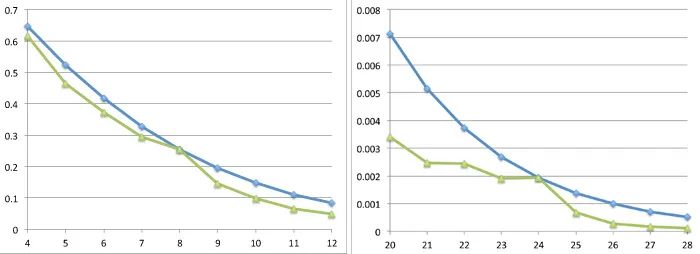
这里值得注意的是8维和24维,它们上界和下界几乎重合。如果真是重合的,那我们实际上就知道了对应维度的球体堆积常数。科恩和艾尔基斯没能证明它:因为存在某种非常不爽的可能性,球体堆积常数介于上下界之间肉眼无法分辨的微小的缝隙中。科恩在《美国数学会通告》(Notices of the American Mathematical Society)发文说:"对于信仰数学之美的人来说,这应该不可能,但信仰不是证明。"
缝合缝隙
维娅佐夫斯卡在科恩和艾尔基斯的工作基础上,缝合了8维空间上的缝隙。随后,又在科恩、库马尔(Abhinav Kumar)、米勒(Stephen D. Miller)、拉德申科(Danylo Radchenko)的帮助下,完成24维的工作。如果忽略球体本身这个形状,只考虑球心,那你就得到了点在空间中的配置。除了每个点的坐标,我们用点与点的距离统计来描述这个配置:产生的最小距离有哪些,它们占比多少?
这是物理学中经常用的办法。"天文学家经常干这种事情,"维娅佐夫斯卡说。"他们观测星空,计算恒星之间的距离。他们忽略空间的几何形状,只记录每两个恒星之间的距离。实际上,这些距离的统计数据一定会满足某种限制。如果你想让一定数量的恒星保持这种距离,又有一定数量的恒星保持那种距离,还有一定数量的恒星保持再一种距离,那么空间中可能不会出现这种恒星排布。"
用类似的思想,科恩和艾尔基斯证明了球体堆积的距离分布也需要满足特定的限制,这让他们得到了球体堆积常数的上界。要完全满足这种限制,你需要找一个性质非常特别的函数,这就是难点。科恩和艾尔基斯只能逼近这个函数,这就是他们只能从逼近层面得到上界的原因。
为了求出8维(以及之后的24维)的球体堆积常数,维娅佐夫斯卡就需要更进一步。它必须找到一个“神奇函数”。这个函数不仅仅是只能估计上界,这个上界必须是不多不少的那种,就是说,它正好等于8维空间中的球体堆积常数。科恩和艾尔基斯认为,这个函数肯定存在,但没办法求出来。"那个神奇函数似乎来自虚空,"科恩在文章中提到。
这就是维娅佐夫斯卡真正实现的东西:用了一个前人从没考虑过的“大胆构造”,它做出了一个满足条件的函数。
维娅佐夫斯卡证明了8维空间中球体堆积常数是:
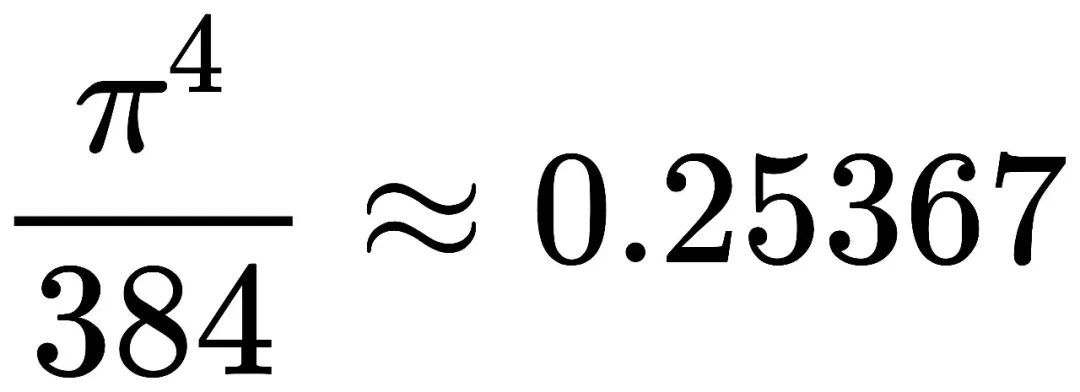
就是说等体球体最多能填充25%左右的8维空间.
使用的填充方法叫做E8格球体填充。所用的球体半径都是1/√2,球心是全部格点(坐标都是整数的点)以及两个格点连线的中点(还要求格点端点的所有坐标值之和为偶数)。E8格和E8例外李群有关系。在8维空间里,就没办法图形展示了。24维空间用的是利奇格(Leech lattice)堆积,比E8格要复杂,得到24维空间的球体堆积常数是
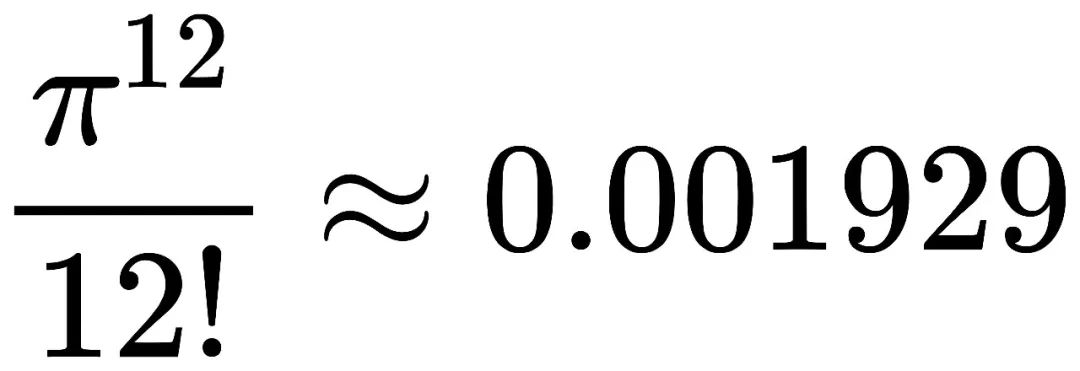
迷之维度
到底是什么让8维和24维如此特别?"每个人都问我这个问题——我也不知道,这是个迷,"维娅佐夫斯卡说。"在这两种维度中,那些点能被精妙的配置,使得我们能精确的计算出来,但这样性质良好的配置其他维度都没有。你问我原因,我真不知道。"
但是已经够了,就8维和24维的证明已经足以让维娅佐夫斯卡获得数学界的至高荣誉了。未来,无论谁用何种方法解决其他维度的情况,都能为这个人带来极高的荣誉。
关注 哆嗒数学网 每天获得更多数学趣文
原文作者:Marianne Freiberger 、 Rachel Thomas
编译作者:Math001
关注 哆嗒数学网 每天获得更多数学趣文
哆嗒数学网
这里是数学爱好者之间分享数学经验、数学心得的数学文化家园。欢迎一切对数学具有浓厚兴趣或疑问的人们。在这里,你不必担心成为绝望的孤岛独思者。这里有千千万万的同伴,陪你一同在数学海洋里畅游。
346篇原创内容
公众号
维娅佐夫斯卡(Maryna Viazovska)是2022年菲尔兹奖得主之一。菲尔兹奖每四年颁发一次,只颁发给40岁以下的数学家,被誉为数学界的最高荣誉之一。
维娅佐夫斯卡是史上第二位女性菲尔兹奖得主,她获奖的成果和我们日常生活中经常见到的一些事物有关。

从桔子开始
运水果的确不是一件轻松的事情。不仅水果会经常被挤变形,即使不考虑变形,把桔子考虑成最简单的球形,也会有问题。无论你怎么装箱,都会留下缝隙。这就自然的会提出一个几何问题:我们如何排布这些球状水果,能让水果尽量多的装到箱子里?比如怎么样装桔子,可以让桔子占箱子里的空间比率最大?
"假设有个巨大的箱子以及数量巨多的球体,"维娅佐夫斯卡说,"同时简化一下问题,球体是刚性的不能被挤压,另外每个球都是相同大小。我们要尽可能多的在箱子里放置这些球。"
如果盒子很小,那么答案可能和盒子的形状有关。但如果盒子很大,形状的影响可以忽略不计,答案只取决于盒子的体积。“这在直观上很显然,存在一个最大的可以用等大小球体填充的体积比,虽然在数学上需要做一些工作才能证明这一点。” 球体堆积问题就是找到这个最高比率,也称为球体堆积常数。

再来一个更简单的例子,让我们降低一个维度:我们不是将球体排布到3维空间中,而是将圆盘排布到2维空间中。“在2维空间中,最佳排布是蜂窝状排布,”维娅佐夫斯卡解释说。通常的蜂窝每个单元都是六边形,六边形整齐地组合在一起,彼此之间没有空间。如果您以相同的模式排布圆盘,您确实会出现间隙,我们能证明这的确是最密集的排布“这样,我们就用这些同样大小的圆盘覆盖了 90%多一点的面积 。”实际上二维球体堆积常数的精确值为
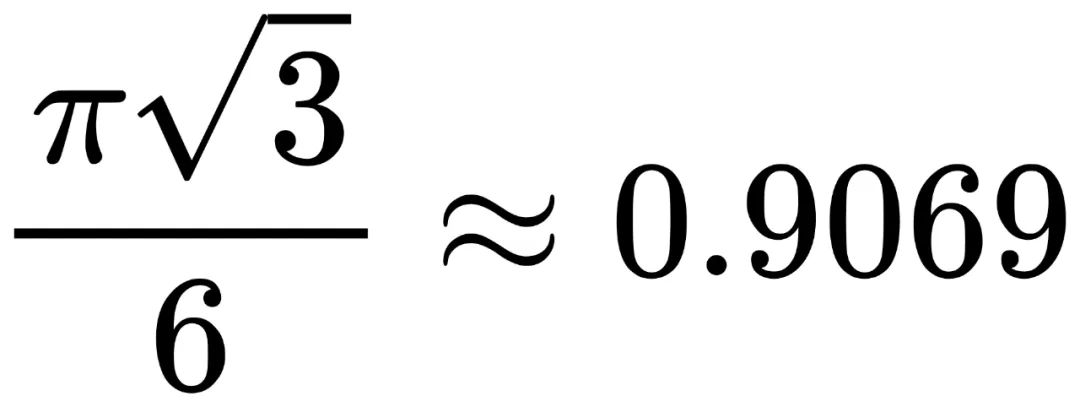

"三维空间的情形被称为开普勒猜想,已经400多年没有解决了,"维娅佐夫斯卡说,"三维空间里我们不止一个最佳堆积,我们有很多比率相等的最佳堆积。"其中一种你在菜市场也见过,就算把桔子摆成金字塔的形状(见上图,我们用球代替桔子)。这种方式的堆积密度大约是74%。实际上三维球体堆积常数的精确值为
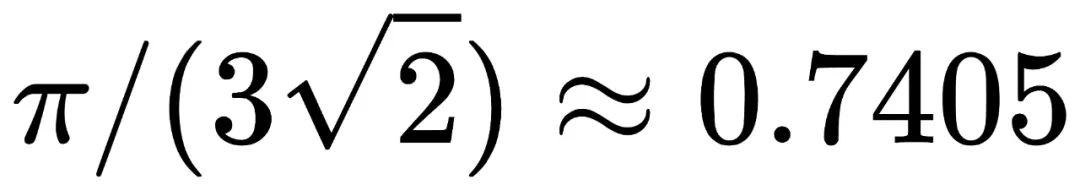
1998年有一位数学家给出了这种堆积是最佳堆积的证明。海尔斯(Thomas Hales)用250页的传统形式的数学论文,加上3GB的计算机代码和数据做计算试图证明它。这是富有争议的证明方式,因为没人能在有生之年去验证计算机产生的数据,所以海尔斯工作是否是完成了证明还没有最终确定。也有专家团队说有99%把握确认这套证明是对的,他们使用了计算机形式逻辑参与验证。
高纬度的球体堆积
不用计算机,只用几页纸,维娅佐夫斯卡给出了最牢靠的证明。这是在高维空间的球体堆积证明,即 8 维和 24 维空间。这样的工作似乎除了烧坏你的脑袋并没有什么别的用处,但事实并非如此。高维空间中的球体堆积在通讯技术中非常重要。它能确保我们通过互联网、卫星、电话传输信息的时候,传输过程有干扰的情况下,也能理解传过来的信息。
为了把控更高的维度,我们要从二维转向三维,我们把思绪再次回到中学阶段。如果你也是那种三维立体图形画图困难户,那你就要感谢代数的作用了。三维空间中的点由3个坐标值表示,线和平面等形状用相应的方程表示。如果你无法想象图形之间的关系,这些方程可以帮到你。
在高维空间中,也适用同样的原理。n维空间的点由n个坐标值表示。和2维以及3维空间一样,你可以给出高维空间中距离和体积的概念,然后定义包括高维球之类的各种形状,这些都是用方程来定义。虽然这些图形无法作图了,但是用代数方法可以处理它们。所以,你同样可以定义高维空间中球体堆积以及堆积密度的具体含义。
回到2维和3维的情形,我们来看看如何从2维的情况推广到3维:先用刚才2维上的蜂窝排布的方式把3维的球体在平面上铺一层,从2维角度看,这是最佳堆积。然后在这一层上铺第二层,第二层的球都铺在第一层的凹陷处。然后继续第三层、第四层……这样的确会产生一个最佳堆积,所以人们会想当然的认为,这种推广方式会自然的推广到高维情形。
哎呀,但事与愿违。知道其中一个维度的最佳堆积和对推算下一个维度的最佳堆积并没什么用。下图展示了4维到26维目前人们知道的最佳的堆积的下界。从图上看,呈指数级下降趋势。

寻找上界
我们寻找的数是某种意义的最大值,比如说堆积密度的最大值。但是,往往没那么好的运气说找到就找到,这时候我们就要退而求其次,去找一个上界:一个数,那个还没求出的堆积常数一定不超过这个数。
不同维度的堆积常数上界陆续被人们提出。2003年科恩(Henry Cohn)和艾尔基斯(Noam Elkies)研究出了一个非常有趣的求上界的办法,可以用于任何维度的计算。但这个办法有实际操作上的难度,所以两个人也只把这些上界算到32维的情况。结果就是下图,包含4到28维的情况,绿色是下界,蓝色是上界。

这里值得注意的是8维和24维,它们上界和下界几乎重合。如果真是重合的,那我们实际上就知道了对应维度的球体堆积常数。科恩和艾尔基斯没能证明它:因为存在某种非常不爽的可能性,球体堆积常数介于上下界之间肉眼无法分辨的微小的缝隙中。科恩在《美国数学会通告》(Notices of the American Mathematical Society)发文说:"对于信仰数学之美的人来说,这应该不可能,但信仰不是证明。"
缝合缝隙
维娅佐夫斯卡在科恩和艾尔基斯的工作基础上,缝合了8维空间上的缝隙。随后,又在科恩、库马尔(Abhinav Kumar)、米勒(Stephen D. Miller)、拉德申科(Danylo Radchenko)的帮助下,完成24维的工作。如果忽略球体本身这个形状,只考虑球心,那你就得到了点在空间中的配置。除了每个点的坐标,我们用点与点的距离统计来描述这个配置:产生的最小距离有哪些,它们占比多少?
这是物理学中经常用的办法。"天文学家经常干这种事情,"维娅佐夫斯卡说。"他们观测星空,计算恒星之间的距离。他们忽略空间的几何形状,只记录每两个恒星之间的距离。实际上,这些距离的统计数据一定会满足某种限制。如果你想让一定数量的恒星保持这种距离,又有一定数量的恒星保持那种距离,还有一定数量的恒星保持再一种距离,那么空间中可能不会出现这种恒星排布。"
用类似的思想,科恩和艾尔基斯证明了球体堆积的距离分布也需要满足特定的限制,这让他们得到了球体堆积常数的上界。要完全满足这种限制,你需要找一个性质非常特别的函数,这就是难点。科恩和艾尔基斯只能逼近这个函数,这就是他们只能从逼近层面得到上界的原因。
为了求出8维(以及之后的24维)的球体堆积常数,维娅佐夫斯卡就需要更进一步。它必须找到一个“神奇函数”。这个函数不仅仅是只能估计上界,这个上界必须是不多不少的那种,就是说,它正好等于8维空间中的球体堆积常数。科恩和艾尔基斯认为,这个函数肯定存在,但没办法求出来。"那个神奇函数似乎来自虚空,"科恩在文章中提到。
这就是维娅佐夫斯卡真正实现的东西:用了一个前人从没考虑过的“大胆构造”,它做出了一个满足条件的函数。
维娅佐夫斯卡证明了8维空间中球体堆积常数是:
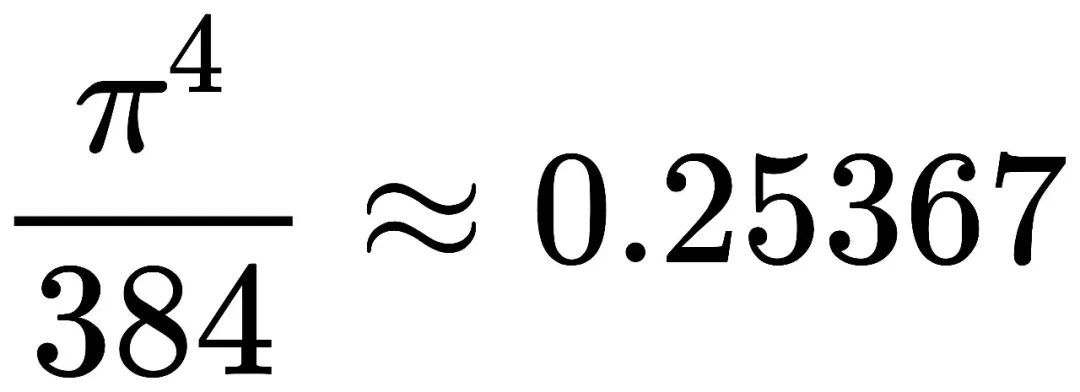
就是说等体球体最多能填充25%左右的8维空间.
使用的填充方法叫做E8格球体填充。所用的球体半径都是1/√2,球心是全部格点(坐标都是整数的点)以及两个格点连线的中点(还要求格点端点的所有坐标值之和为偶数)。E8格和E8例外李群有关系。在8维空间里,就没办法图形展示了。24维空间用的是利奇格(Leech lattice)堆积,比E8格要复杂,得到24维空间的球体堆积常数是
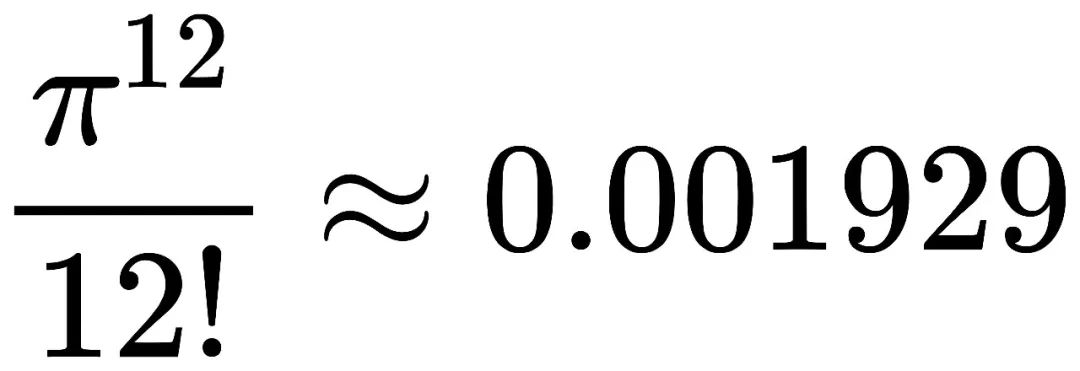
迷之维度
到底是什么让8维和24维如此特别?"每个人都问我这个问题——我也不知道,这是个迷,"维娅佐夫斯卡说。"在这两种维度中,那些点能被精妙的配置,使得我们能精确的计算出来,但这样性质良好的配置其他维度都没有。你问我原因,我真不知道。"
但是已经够了,就8维和24维的证明已经足以让维娅佐夫斯卡获得数学界的至高荣誉了。未来,无论谁用何种方法解决其他维度的情况,都能为这个人带来极高的荣誉。
关注 哆嗒数学网 每天获得更多数学趣文