下雨没伞:跑还是不跑?
原文作者:Atheeta Ching,伦敦大学学院数理生态学博士。
译文作者:radium,哆嗒数学网翻译组成员。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
编者按: 有一个故事,说下雨天,大家都拼命的在雨中跑。有一个人却慢慢的走,别人问他为何不跑,他说,你没看见前面也在下雨吗,跑有用吗?很多人都是把这人当笑话来看的,但是这篇文章告诉你,问题没那么简单!
很多事情都影响着我们的生活,其中一件事便是天气,特别是下雨天未带伞(或者我们懒于将伞从包里拿出来)时的窘迫。凭直觉就知道似乎奔跑就是最好的选择,或者至少我们走快一点,就可以少淋一些雨。但是这也意味着雨点会以更快的频率从正面打在我们身上。
所以,如何才能让雨点在我们衣服上画的地图的面积少一点呢?这个问题实际上在过去的几十年里被众多的专家或爱好者们讨论过,无论是数学杂志还是像《流言终结者》这样的科普电视节目(事实上他们关于这个问题做了两期节目,第二期是对它的更正)。
让我们从最简单的模型开始,想象雨点匀速竖直落下。在图中,你就是那个灰色的长方形(因为下雨让你的心情不好,灰色可以表达这点心情)。
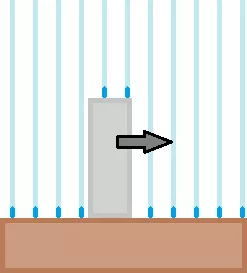
同时我们也要假设雨点均匀降落,其次第二个假设是假设雨点只从人的头上落下,而不考虑打在身上的情况。在这种情况下,无论雨点下落的速度有多快,你最好的选择便是“跑”。跑的越快你在雨中所淋到的雨越少。
好了,现在我们考虑,如果雨点因为风的缘故以一个角度降落在你身上又会如何呢?对于这个问题我们将会介绍一些真正的数学。和前面一样,我们将假设雨速度为定值Vr均匀下落。
雨域是这个问题的一个很重要的概念。这个区域包含了所有将会淋到你身上的雨点的初始位置。假设你以s的速度运动,因此在二维图上你的速度可以表示为向量Vu=(s,0),这使得你在雨中花费的时间为1/s。
在你身上取一个点P,在雨域取一点Q,在t时刻后在这一点上的雨点会淋到你身上。然后我们就可以得出出雨点会在Q + Vr·t这一点上淋在你身上。而你的原始位置P可以表示成为 P=Q + Vr·t − Vt·t。从而对于每一个你暴露在外可以淋到雨的位置P,对任意时间t∈[0,1/s],点P+(Vr−Vt)·t在雨域内.
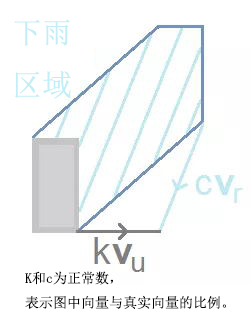
完整的下雨的区域由这些斜线勾勒出来了。每一条斜线的长度为 ||Vr−Vt||/s。这样就十分清晰了:如果雨以一定的角度下落,你应该跑的越快越好,缩短雨域的水平长度(下雨区域内的“宽”是定值,而和人的身高成比例)。
要是雨从你背后方来,又会怎样呢?这样一来,事情变得有一点复杂。雨点速度的分解为Vr=(V1,V2),因为雨点有向前方的速度,因此 V1>0。于是一些不同事情将会发生(假设雨以一定的速度均匀下落)。之前我们提到,你以速度s移动。如果s>V1你就不会被你背后的雨淋到,但是你的头部和你身体的正前方会被淋到。
如果 s=V1,也就是说,你的速度和雨在你前进方向的速度一样,那么仅仅只有你的头部会被淋到雨。最后,如果s<V1显然你的背部和头部会被淋到雨,但是你的身体的正面会保持干燥。令Af为你身体正面或背面的暴露在雨中的面积,而At为你头部暴露在雨中的面积。
在我们之前的二维案例中,这些只是表示你所代表的长方形的高度和宽度。雨点淋湿的这些部分的总量分别正比于Rf =|V1−s|·Af 以及 Rt=|V2|·At。
上述中在雨中的时间为1/s,被雨淋湿的函数为R,正比于:
R1(s) = [(V1 - s)·Af + |V2|·At]/s 若 s≤V1
R2(s) = [(s- V1)·Af + |V2|·At]/s 若 s>V1
其中比例的乘子是雨的密度。注意这个函数可以被应用到之前的例子。即雨点向后方下落,V1<0。我们发现我们总会有R=R2,因此让R最小化的方法便是尽可能地增加s。
雨点向前落下的例子中我们有V1>0. 让C = -V1·Af + |V2|·At 然后注意到R是连续的R1是一个关于s的减函数,而R2的变化依赖于C的正负。
如果C>0,R2也是关于s的减函数,要取R的最小值,那么s应该增加到最大值。
如果C=0,R2是一个常值。我们可以通过取任意的s≥V1来最小化R
如果 C<0,R2是一个关于s的增函数,那么我们仅仅只能通过让s=V1来最小化R。例如:你精确地于雨水平分量相同的速度奔跑。
C依赖于你的体格和在雨中的速度。如果雨向前方的速度很小,那么你最佳的选择任然是尽可能快的跑。但是,如果雨向前的速度很大,使得C<0,那么你最好精确地于雨水平分量相同的速度奔跑。同时也意味着雨点会打湿你的头部,但这些都是理论上讲的情况。
关于这个问题还有很多复杂的模型,考虑不同的形状(不是正方形的情况下)或者突然来阵一阵大风,都会影响最终的结论。最后,我们将以Matthew Wright(很遗憾不是之前Chalkdust的成员)写的五行打油诗来结束。
固执的青春
暴露在雨中的执拗
若雨从背后拥抱
我我便与雨同行
但若迎风而行
最华丽的步调
便是与雨赛跑
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

评论已关闭