图说行列式:几张图让你明白行列式的性质
作者,【陌生,爱),哆嗒数学网群友,就读于湖北理工学院。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
今天小编想给大家讲一下行列式,诸位看到行列式是不是觉得特别亲切,大一的时候学习行列式有没有很痛苦啊?——反正当年小编学习这个是及其痛苦的——也许我比较笨吧,:)。
是否还记得《线性代数》或者《高等代数》里面的行列式定义?一般的教材对行列式的定义大概两种吧,逆序定义和展开式定义,无论哪种定义方法,都让我当你感觉莫名其妙,一直要到很后面学习了线性方程组,建立了方程与行列式的联系,才知道这些定义的意义。在没有任何直观意义的帮助下,学习行列式的各类性质简直和死记硬背没有区别。
今天小编抛开这些通常线性代数或者高等代数教材上的定义,从几何上让读者们更直观的理解什么是行列式,并用几何方法来介绍行列式的基本性质。
那我们现在开始来说说行列式吧!首先来看简单的二阶行列式:
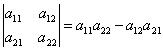
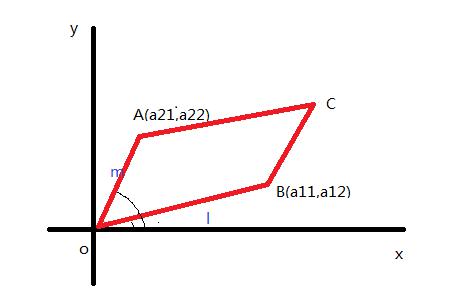
如上图,平行四边形OACB的面积为:
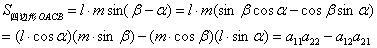
毫不意外的(取m = l = 1),我们用这种方式来记忆和角公式:
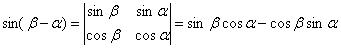
因此二阶行列式的值,可以表示两个向量所构成的平行四边形的面积。那么三阶行列式表示什么含义呢?n阶行列式又代表什么含义呢?类推一下相信大家就能想出来。没错三阶行列式的几何意义为三维欧式空间里平行六面体的体积。当然n阶行列式就由n个n维向量组成,其结果为n维平行多面体的体积。
下面的文字我们将来解释行列式基本性质的几何意义了。下面我们一起来看行列式性质的几何解释,这里我们取二阶或者三阶行列式进行说明。
性质1:行列互换行列式不变(转置)。
数学语言表述为:
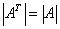
几何解释:很显然平行四边形两条邻边互换,它的面积依然不变。
这说明行列式的行和列等价,也就是说凡是对行成立的性质,对列也成立。
性质2:以一常数乘行列式的一行就相当于用这个数乘以此行列式。
数学表述为:
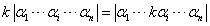
对于二阶行列式,我们看上图就很直观,我们将其中一个向量变成原来的k倍,面积也跟着变成了原来的k倍。
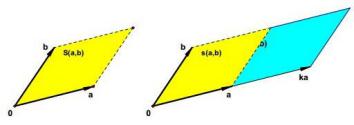
类似的三阶行列式有,平行六面体体积的k倍相当于其中一个向量变成原来的k倍。平行六面体体积的增大可以看成其中某个棱长增大相应的倍数。
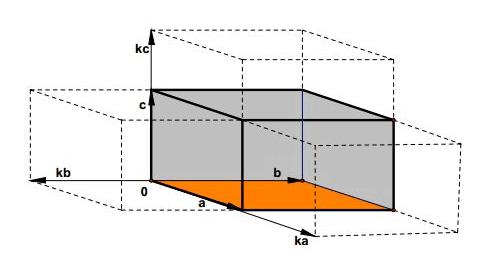
性质3:如果某一行是两组数的和,那么这个行列式就等于两个行列式的和,而这两个行列式除这一行以外全与原来的行列式对应的行一样。
数学表述为:
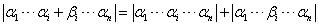
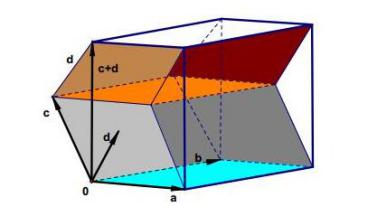
如图所示,图中的紫色平行六面体的体积可以看成两个小平行六面体的体积之和,也就是说一个行列式可以通过拆分其中的一个列向量得到两个行列式的和。
性质4:如果行列式两行成比例那么行列式为零。
数学表述为:
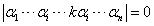
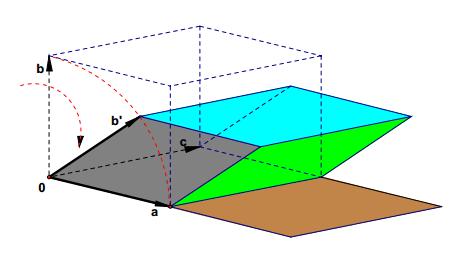
先考了特殊情形,当k取1时,也就是说行列式有两列或者两行元素相等时,它所对应的空间平行六面体的两条邻边重合,相应的就是将平行六面体压成高度为零的二维平行四边形,其体积为零,即行列式为零。当k不等于1时,相对应这组向量里面有共线的向量,即由n维降低到n-1维,对应的度量体积为零。
性质5:把一行的倍数加到另一行,行列式不变。
数学表述为:
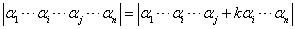
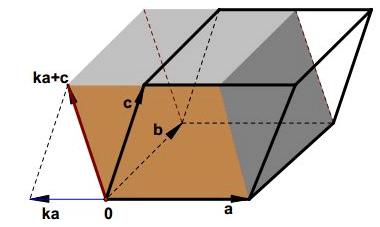
这条性质表述为,以向量a和b为底的平行六面体在向量a方向上做切向变换。我们知道将平行六面体平推它的体积依然不变。故对应行列式的值不变。
性质6:对换行列式两行的位置行列式取反号。数学表述为:
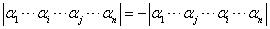
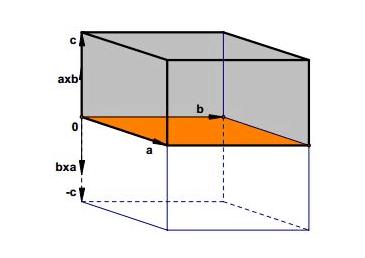
因为向量具有方向性,如果我们把符合右手定则的向量积定义为正值的话,则它的反向定义为负值。当det(A)为负值时它就确定了原像的一个反射。
其实一个行列式的几何意义是有向线段(一阶行列式)或有向面积(二阶行列式)或有向体积(高阶行列式)。行列式是由各自坐标轴上的有向线段所围起来的有向体积的和。这就累加要注意方向,同向相加,反向相减。
相信读者应该理解了行列式的几何意义了吧,是不是对行列式有了更新的认识啊?其实小编一直的觉得很多数学量或者数学概念,都可以找出它所对应的直观意义,这样我们的数学学习就不会那么抽象那么难理解了,反而会很有意思。
最后希望大家能喜欢数学,反正小编就很喜欢数学——数学虐我千百遍,我却待它如初恋——不管你信不信,反正我自己都不信,啊哈哈哈哈~~~。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

评论已关闭