如果数轴有两个原点会怎么样？

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

你即将搬家，所以你得在子事先没有过目的情况下租一个新的公寓。你网上也找了，电话也打了，终于相中了一个看上去不错的房子。但你到了你的新家的时候，总觉得有的地方…昏暗无比。实际上，房间所有地方都黑漆漆的，因为根本没电。你重新去翻看房屋出租的广告，的确，广告没有任何地方强调了房间就通电的，但你不会考虑你需要将这件事情当成一个问题去询问房东。

 

对于很多数学家来讲，豪斯多夫性质就像一个房间就应该通电一样自然。当然，你能构造一个不是豪斯多夫的空间，但你研究问题的时候，多少会认为，一个正在思考的空间是豪斯多夫的。在一个不是豪斯多夫的空间里做拓扑问题，那种感觉和在一个乌漆嘛黑的房间里乱撞没有区别。豪斯多夫性质是以德国数学家费利克斯·豪斯多夫的名字命名的。豪斯多夫性质描述的是数学空间中关于分离性的众多性质中的一个：空间中的点，它们之间的的分离程度到底有多大？一个拓扑空间是豪斯多夫的意思是，任意两个空间中不同的点，都能把它们分别放入两个不相交的开集里面。开集是拓扑空间中最基本最普遍的概念，你可以看看我们之前的文章，来了解一下为什么开集如此重要。

 

为了进一步了解豪斯多夫性质的重要性，我们来思考一些常见的空间，比如说实数轴。实数轴中的开集就是那些开区间(编者注：以及开区间并起来得到的并集)，比如(0,1)。两个数轴上的点，无论他们距离有多近，他们之间总有一个距离区隔，所以我们能找到两个足够小的开区间，这两个开区间各自包含了一个点，并且这两个区间没有重叠的部分。
 

 

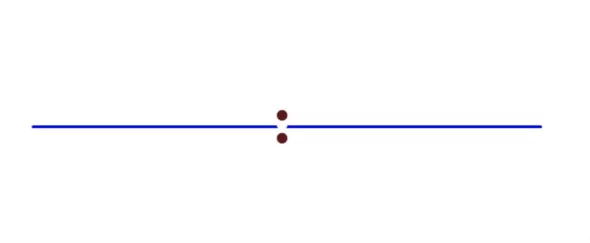
其他常见的空间——诸如二维欧氏平面、三维欧氏空间——同样具有这个性质。我们似乎有点难以想象一个空间没有这样的性质。这里我们来引出一个有两个原点的数轴——最简单的没有豪斯多夫性质的空间之一。

 

 

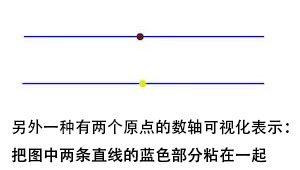
为了作出一个有两个原点的数轴，我们从作普通的两个数轴开始做工作。我们标记好两个普通数轴上的点，上面那条数轴的点为(x,0)，下面那条上的点为(x,1)。现在，我们说我们把除了x=0以外的所有的(x,0),(x,1)这样的点都看成相同的点。而且我们设定，新的空间继承之前那两条普通数轴的通常拓扑，就是说，新空间的开集还是由那些开区间组成。

 

你可能无法接受我们把那样的两个点看成相同点的设置，但是思考拓扑问题的时候我们必须设定一些类似这样的规则。就像乔治·奥威尔的小说《一九八四》中设定“我们和东亚国的战争永无完结”（We have always been at war with Eastasia）一样，(1,0)和(1,1)在我们的设定中就是相同的点。

 

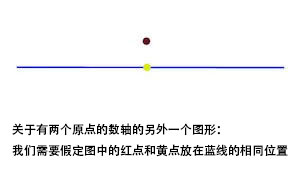
你能明白有两个原点的数轴不是豪斯多夫的原因吗？毫无疑问，定义中“除了x=0”引起了我们的注意。在上面的那条数轴中，每个包含(0,1)点的开区间，都和下面数轴中包含(0,1)的开区间有重叠的部分，这是因为两条普通数轴中，几乎所有的点都是相同的点。

虽然，我在本文中画了一些图形，但是仍然难以用准确的图形展示有两个原点的数轴。实际上，我们能在数学上证明我们不可能画出有两个原点的数轴，这也是豪斯多夫性质之所以重要的原因之一。一个没有豪斯多夫性质的空间是很难直观的展示的。但是一个空间如果满足豪斯多夫性质，那么我们就可以以某种适宜的方式将它纳入到某个欧氏空间，或者维数再高一些的空间中讨论。两个原点的数轴不能嵌入到任何一个欧氏空间来展示它的本质。于是，我们退而求其次，我们在纸上或者电脑屏幕上作图的时候，会省略掉一些点和线，希望读者能大致能理解。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa