数学与统计学竟如此不同

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

原文作者，Bai Li，就读于多伦多大学计算机科学学院。

翻译作者，豆浆，哆嗒数学网翻译组成员。

校对，小米。

 

 

 

 

统计学与数学有着某种有趣而奇特的关系。在很多大学的院系，它们都是混合成“数学与统计系”。其他时候，统计学被归为应用数学中的一个分支。纯数学家倾向于把统计学看作是概率论的应用，或是因为它“不够严谨”而不喜欢。

 

 

在研究了这二者之后，我认为说统计学是数学的一个分支是错误的。相反，统计学是一门独立的学科，它使用数学，但与其他数学分支（如组合数学或微分方程或群论）有本质的区别。统计学是对不确定性的研究，而这种不确定性渗入到整个学科，以至于数学和统计学是根本不同的思维方式。

 

 

 

 

 

 

数学总是遵循固定的的定义——定理——证明的结构。无论你研究哪一个数学分支，无论是代数数论还是实分析，数学论证的结构或多或少是相同的。

 

 

你首先得定义一个对象，就说wug吧。在定义之后，每个人都可以看一下定义，并就哪些对象是wug和哪些对象不是wug达成一致。（编者注：wug是心理学家Jean Berko在她的实验中虚构的一种动物）

 

 

接下来，你继续证明关于wug的有趣的事情，使用奇妙的论证，如反证法和归纳法证明。 在证明的每一个步骤，读者都可以证实，这一步在逻辑上是从定义出发的。经过几次这样的证明之后，你现在已经了解了大量关于wug的性质，以及它们如何与数学宇宙中的其他物体相联系的，每个人都很愉悦。

 

 

在统计学中，用直觉和例子来定义事物是很常见的，即是说“所见即所知”，很少像数学里那样黑白分明。这是出于一个必然的理由： 统计学家用真实的数据来工作，这些数据往往是混乱的，并不容易理清，也难以从严格的定义来研究。

 

 

以“异常值”的概念为例。当数据包含异常值时，很多统计方法表现不佳，因此识别异常值并将其剔除是一种常见的做法。但是究竟是什么构成了异常值呢？好吧，这取决于许多标准，比如你有多少个数据点，它距离其他点有多远，以及你在拟合什么样的模型。

 

 

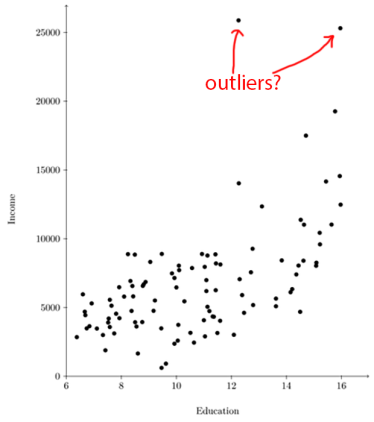
在上面的图中，那两点可能是异常值。你应该剔除它们，或者保留它们，或者可以剔除它们之一吗？没有正确的答案，你必须自己判断。

 

 

又如，考虑p值。在很多时候，当p值低于0.05时，可以认为是统计学显著的。但这个值仅仅是一个指导值，而不是一个必须遵守的规则——不是说0.048就是显著的而0.051就不显著。

 

 

现在让我们假设你在运行AB测试，并且发现将按钮更改为蓝色会导致更高的点击次数，p值为0.059。你应该建议你的老板做这个改动吗？如果你得到0.072或者0.105呢？在哪一点它就会变得不显著呢？没有正确的答案，你必须自己判断。

 

 

再举一个例子：异方差。这是一个奇特的词，这意味着你的数据集的不同部分的方差是不相等的。异方差是不好的因为很多模型假设方差是常数，如果这个假设被违反，那么你就会得到错误的结果，所以你需要使用一个不同的模型。

 

 

 

 

 

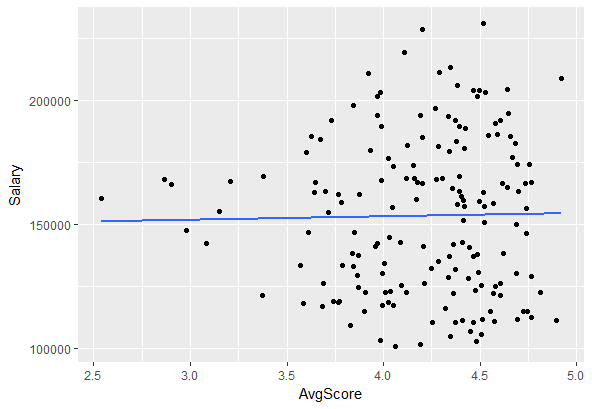
这个数据是异方差的，还是只看起来差异是不均匀的，因为3.5的左边有那么几个点？这个问题是否严重到拟合线性模型是无效的？没有正确的答案，你必须自己判断。

 

 

另一个例子：考虑一个有两个变量的线性回归模型。当你在图上绘制点时，你应该会期望这些点会大致落在一条直线上。当然，不完全是在一条线上，只是大致线性。但是如果你得到这个：

 

 

 

 

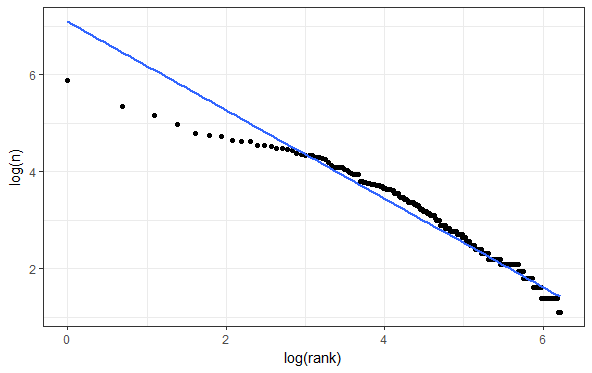
有一些证据表明这里有非线性，但是你需要多少“弯曲程度”，才能让你觉得这绝对不是“大致线性”以至于你必须使用一个不同的模型？再说一次，没有正确的答案，你必须自己判断。

 

 

我觉得你发现其中的规律了。在数学和统计学中，都是只有在某些假设得到满足的情况下，才有模型。然而，与数学不同，在统计学里，没有通用的程序可以告诉你数据是否满足这些假设。

 

 

以下是统计模型的一些常见假设

 

 

1、 随机变量服从正态（高斯）分布

 

2、 两个随机变量相互独立

 

3、 两个随机变量满足线性关系

 

4、 方差是常数

 

 

你的数据不会完全符合正态分布，所以所有的这些都是近似值。统计学里有一个普遍的说法：所有的模型都是错的，但是有些却是有用的。

 

 

另一方面，如果你的数据与你的模型假设有很大的偏差，那么这个模型就会崩溃，你会得到没用的结果。没有通用的黑白分明的程序来决定你的数据是否正态分布，所以在某些时候你必须介入并应用你的判断。

 

 

另外：在这篇文章中，我忽略了数理统计，它是统计学的一部分，试图用严格的数学来证明统计方法的合理性。数理统计遵循定义-定理-证明的模式，与数学的其他分支非常相似。你在统计课程中看到的任何证明可能都属于这个类别。

 

 

 

 

你可能会想：没有严格的定义和证明，你如何确定你所做的一切是正确的？事实上，非统计学（这里指数学）和统计学方法有不同的判断“正确性”的方法。

 

 

非统计方法使用理论来证明其正确性。例如，我们可以通过归纳法证明Dijkstra算法总是返回图中的最短路径，或者快速排序法总是按排序顺序排列数组。为了比较运行时间，我们使用大O符号，这是一个用于严格化程序运行时间的数学结构，它刻画的是当程序的输入趋于无穷大时运行时间的行为

 

 

非统计算法主要关注最坏情况分析，即使是近似和随机算法。对于旅行商问题，最好的近似算法的近似比率为1.5 - 这意味着即使对于最差的输入，该算法的路径也不超过最优解决方案的1.5倍。算法是否在大多数实际输入中执行得比1.5好很多都没关系，因为它总是我们关心的那个最糟糕的情况。

 

 

如果能够对现实世界的数据进行推断和预测，那么这个统计方法就是好的。一般来说，统计学有两个主要目标。首先是统计推断：分析数据以了解它产生的过程; 其次是预测：使用历史数据的模式来预测未来。因此，在评估两种不同的统计算法时，数据至关重要。没有多少理论能告诉你支持向量机是否比决策树分类器更好 - 唯一的办法就是在你的数据上面运行这两个算法，看看哪一个能给出更准确的预测。

 

 

 

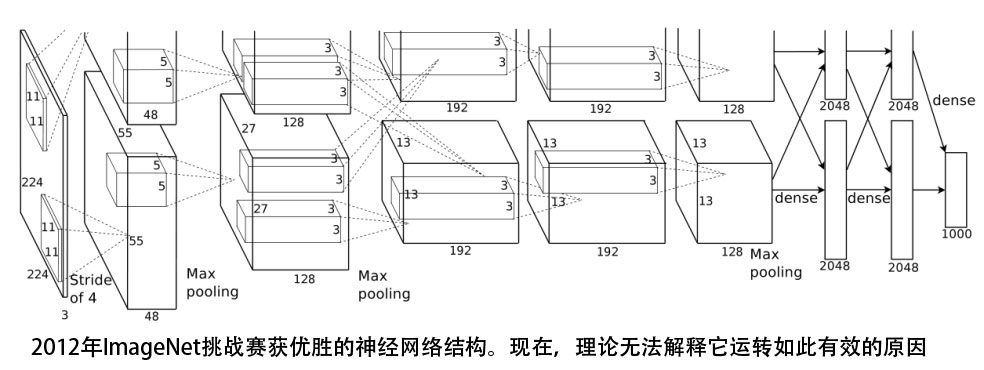
在机器学习方面，还有一些理论试图形式化地描述统计模型的行为，但是它们离现实应用还有较大距离。 例如，考虑VC维和PAC可学习性的概念。基本上，在理论给出的条件下，因为你提供了越来越多的数据，模型最终会收敛到最好的一个，但不关心你需要多少数据才能达到期望的准确率。

 

 

这种方法对于决定哪种模型最适合于特定数据集是非常理论化和不切实际的。在深度学习中，理论尤其短缺，可以通过反复试验找到模型超参数和体系结构。即使是理论上已经很好理解的模型，这个理论也只能作为一个指导原则; 你仍然需要交叉验证来确定最佳的超参数。

 

 

 

数学和统计学都是我们用来模拟和理解世界的工具，但它们以非常不同的方式实现。数学创造了理想化的现实模型，里面一切都是清晰的和确定的；统计学认为所有的知识都是不确定的，并且试图理解数据尽管一切都存在随机性。至于哪种方法更好——两个方法都有其优势和劣势。

 

 

数学对于规则是合乎逻辑的并且可以用方程来表示的领域进行建模是很好的。其中一个例子是物理过程：只有一小部分规则对预测现实世界中发生的事情非常有用。而且，一旦我们发现了系统遵循的数学规律，它们是可以无限泛化的——即使我们只观察到从树上掉下来的苹果，牛顿定律也可以准确地预测天体的运动。另一方面，数学在处理错误和不确定性方面显得很笨拙。数学家创造了一个现实的理想版本，并希望它与真实的东西足够接近。

 

 

当游戏规则不确定时，统计学就会闪耀它的光芒。统计数据包含不确定性，而不是忽略错误。每一个值都有一个置信区间，在95％的时间内你可以预期它是正确的，但我们永远不可能100%确定任何东西。但只要有足够多的数据，正确的模型就可以从噪声中分离出信号。这使得统计学在处理有许多未知的混杂因素（如模拟社会学现象或任何涉及人类决策的事物）时成为一个强有力的工具。

 

 

缺点是统计学只适用于你有数据的样本空间; 当超出了过去训练数据的范围进行预测时，大多数模型都表现得不好。换句话说，如果我们用苹果从树上掉下来的数据进行回归，它最终会很好地预测从树上掉下来的其他苹果，但是却无法预测月球的轨迹。因此，数学比统计学能使我们更深入，更基础地理解一个系统。

 

 

数学是一个美丽的学科，它能从复杂的系统提炼出本质。但是，当你试图了解人们的行为方式，当主体不总是理性的时候，从数据中学习是一个很好的选择。

 

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa