法诺平面：射影平面、彩票和死亡圣器

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

原文作者，Evelyn Lamb，数学普及作家。

翻译作者，Bibliomania，哆嗒数学网翻译组成员。

校对，donkeycn。

 

 

当我走进圣艾夫斯,
我见到一个平面有七条线,
每条线有三个点,
(但是一共也只有七个点,)

这首诗并不能很好地描述法诺平面（Fano plane）。

以吾之愚见，法诺平面是最小的有趣的空间。这也许能被扯皮归纳地证伪，但是一个点，或者一些孤立点，并不是有趣的例子。

 

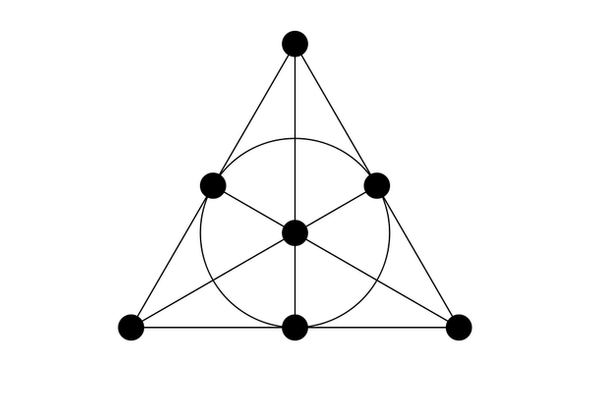
Fano平面有七个分布在七条线上的点。它是射影平面最小可行的例子。

你有没有想过凭什么平面上有些线相交，有些却没有？多么随意啊！不过射影平面就可以把你从这个烦人的问题中拯救出来了，它满足任意两条线都相交。

一个射影平面需要满足下面一些条件。

*每两“点”都有一条“线“连接。
*每条“线”都和其他任何一条“线”相交。
*存在四个点，使得没有一条线过其中两个以上的点。(这个条件并不总是列出来，但是它排除了一些平凡情况，比如说一条线上的两个点或者过一点的几条线。)

有时候数学是靠内心的直觉的，比方说你思考射影几何的时候。(公平来讲，有时候射影几何看起来非常直观，毕竟它的一大应用就是在透视画法上。)你可以把欧几里得平面变成射影平面，通过给每个方向的平行线们添加一个它们所相交的“无穷远”点。所以说有水平方向的无穷远点，有垂直方向的无穷远点，有与水平方向成逆时针47.322度角方向的无穷远点等等。接下来你再让这些无穷远点组成无穷远线。如果你好好想一会，就能明白这样是满足射影平面的要求的。

 

如果考虑无穷远线上的无数的点让你感到头晕目眩，那法诺平面就是一个更轻松的替代品。它可以简单地看清楚线和点是怎么相交和交互的。

 

法诺平面是个挑战直觉的东西。当你看到它的图式时，你便会理所当然地认为它有无穷多的点。毕竟它有七条线，我们也都知道，再短的线段，上面也有无穷多的点。

 

噢不，数学是独裁体系，我们都是独裁者。我们说那七个点就是它仅有的七个点。而这里的”线”并不是由”点”构成的，它们只是公理里规定的“线”而已。另外一个反直觉的地方在于有一条“线”看起来像是个圆，至少在大部分示意图里面都是这样。但如果你都已经接受“线”并不是由无穷多点组成的想法了，那也不难让自己承认这圆真的就是“线”。

法诺平面是最小的有限射影平面。你也许想知道别的射影平面可能的大小。如果我们想让每条线上有4个点而不是3个，我们能找到这样的平面吗？令人惊讶的是，指出射影平面可能的大小并不是一个平凡的问题。(关于术语的说明:我们说法诺平面的阶为2，因为每条线有2+1=3个点，每个点在2+1=3条线上。一般地，一个射影平面阶为N，如果每条线有N+1个点，每个点在N+1条线上。阶为N的射影平面有N²+N+1个点。)我们知道存在阶为任意素数以及任意素数的幂的射影平面，但至于其他数字，我们还有很多工作要做。举个例子，直到上世纪90年代，研究者才确切地证明了不存在阶为10的射影平面，而对于12，仍然是一个开放问题。

虽然有限射影平面看上去像是遗世独立的纯理论的典范，但意外的是法诺平面以及相关的东西居然在博彩方面有所应用。我第一次是在Jordan Ellenberg的《魔鬼数学》（How Not to Be Wrong，又译《数学教你不犯错》）中读到有关的东西的。他举了一个从7个数中选3个的彩票的例子。玩家3个数都猜对的话就获头奖，或者猜对两个数得小奖。

 

从7个数中选3个，一共有35种可能的组合，所以说你只有1/35的机会中头奖。不过你可以利用法诺平面来增加你猜中两个数的机会。技巧在于买一些彩票但避免同样的数对出现在两张彩票上。你不会想同时买123和234，因为如果2和3猜中了，而你买了它两次了。虽然这意味着两倍的奖金，但也意味着你在其他数对中奖时什么都得不到。

为了在彩票中利用法诺平面中到奖，给7个点依次标上1到7，接着看每条线上的数字。我得到了123, 147, 156, 246, 257, 345, 367.

 

如果你去验证这些数组，你会发现每个数对都恰好出现了一次。不管中奖的数字是哪些，我们都至少猜中了3个中的两个。如果你标数字的顺序和我不一样，你会得到不同的数组，不过还是有同样的性质。

 

现在并没有多少彩票只选3个数字了，但花点心思再加上电脑的能力，这个想法可以接着延伸。当然，即使是利用射影平面的聪明策略，在实际彩票购买中使用也不大可能合算。不过如果你感兴趣的话，Ellenberg讲过一个Cash WinFall的故事，其奖品好到足以赢得一些MIT学生的钱。

想了解法诺平面与拉丁方，环面拓扑，纠错码以及其他许多领域的联系，可以查看弗吉尼亚理工大学的Ezra Brown的两篇文章……《(7,3,1)不同的形式集锦》和 《(7,3,1)不同形式的更多集锦》。（链接http://www.math.vt.edu/people/brown/doc/731.pdf ，http://www.math.vt.edu/people/brown/doc/731_more.pdf ）

 

如果八元数乘法的让你感到困顿的话，法诺平面也能帮你记住八元数的乘法规则。最后我忍不住提一句，法诺平面看起来和哈利波特中的死亡圣器的标志惊人地相似。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa