血腥杀戮：数学建模还原古战场

 

原文作者，Alex Doak，伦敦大学学院流体力学博士。

翻译作者，溦之洸茫，哆嗒数学网翻译组成员。

校对，我是崔小白。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

希腊：留克特拉 （公元前371年）

出于对至高权力的渴望，古希腊的各城邦总是在不断经历战火的洗礼。在一阵短暂的和平后，当时的霸权斯巴达公然挑战底比斯的政治地位。由于底比斯拒绝解散由其主导重建的彼奥提亚邦联同盟（Boeotian Confederacy），斯巴达对其宣战。底比斯城以及她的盟友聚集了7200名重装步兵（hoplites），由将军埃帕米侬达（Epaminondas）率领，来到了留克特拉的地界，在那里等待他们的是9600名斯巴达重装步兵。

 

此时斯巴达国王克莱奥姆波洛图斯（Cleombrotus）情绪十分阴郁，尽管近期在军事上有过胜利，然而在前往留克特拉的行军路上已经显现了凶兆，尤其是因为献祭给神灵的动物被狼吃了。然而在对手下各个将军进行询问之后，发现他们都确信斯巴达能够取得胜利。现在他召唤你这个奇怪的旅行者，希望通过你的惊人洞察力帮助他分析未来。

 

 

一对一战斗及兰彻斯特线性律

在所有的数学建模中，如果希望得到有意义的结果，我们必须理解所模拟战斗过程的基本机制。在这个例子中，我们需要对古希腊战争有更好的了解。希腊城邦的部队主要是有重装步兵组成。在战斗中，这些人采用的是‘臭名昭著’的方阵队列：士兵们组成数排密集的横向队列，手持长矛和盾牌迎击他们的敌人。每一支部队同时前行，最勇敢和最有战斗经验的军人是在前排，这样才能保证行进的队伍不会减速和逃窜。两军接触后，盾牌互砸，长矛互戳，血肉横飞，尸横遍野……最终，在经受一定的兵力损失后，一方的队形完全崩溃，士兵开始大量逃窜，最终不可避免地被击败。
 

对于这一类的战斗，兰彻斯特首次给出了一个简单的模型，他假设军队的交战是由一对一的形式进行的。也就是说，每名士兵只和与他对应的那一名敌军士兵交战，没有参与打斗的士兵在后排静静等待着他们战斗回合的到来。假设军队数量在时间t内是连续的。斯巴达军队士兵数S(t)及底比斯军队士兵数T(t)的变化率可以表示为：
 

其中，N指的是在某一时间双方各自的交战人数。我们已知克莱奥姆波洛图斯国王的方阵是由希腊重步兵组成的标准12排方阵，那么第一排就有9600/12=800人。同时，克莱奥姆波洛图斯国王认为底比斯军队为了避免侧翼被包抄，会采用同是每排800人的9排的方阵来迎击自己的军队。古希腊时期战斗的一个典型特点是伤亡相对较低，我们可以假设如果任意一方士兵数不足以维持6排阵列（即T＜4800或S＜4800），士兵就会产生恐慌情绪进而逃窜。

K_T和K_S分别表示两只军队的战斗力。如果K_T=1 (K_T表示K的下标是T，下文相应情况类似)，意味着单位时间内，每一位在战斗的底比斯士兵都杀死了一名斯巴达士兵；如果K_T=0，表明没有底比斯士兵杀死斯巴达人。兰切斯特杀伤率（Lanchester attrition rates ，即K_T和K_S）不一定要为常数：它们可以是与时间有关的（战斗进行过程中士兵会变疲劳），或是依赖于S和T的数值（以寡敌众会扼杀士兵的希望，或是使它们更加拼命战斗）。不过，为了简单起见，我们认为这两个参数是常数。

 

那么问题来了：战斗中底比斯人的表现要比对手斯巴达人好出多少才能保证自己取得胜利？

我们建立的耦合系统非常容易求解，用（1）式除以（2）式，得到
 

对上式积分，并将S与T的初值带入，得到
 

 

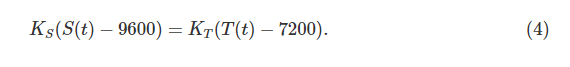
请注意，上述方程体现了军队中士兵数和他们总的战斗力是呈线性关系的（即著名的兰彻斯特线性律）。这是因为我们采用了一对一的战斗模型假设。底比斯要取得胜利，换言之在某一时间t^*(t^*表示t的下标是*，下文相应情况类似),S(t^*)=4800且T(t^*)＞4800，将S(t)=4800带入方程（4），并重新写出T的表达式，代入T(t)>4800，可以得到底比斯取得胜利的条件为
 

 

 
 

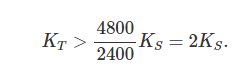
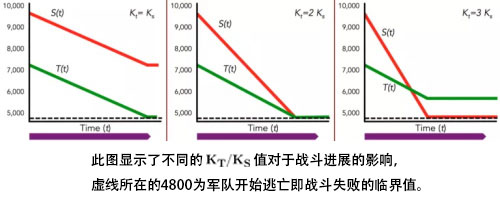
将这些信息呈给克莱奥姆波洛图斯国王，你除了看到他的自信之外并不能提供什么帮助：斯巴达人是当时最勇猛的战士，尽管他的盟军并不是这种最高质量的军队，那也没有理由认为他们会比底比斯的彼奥提亚联合军“弱”两倍。（译者注：这里的弱两倍指K_S/K_T＜0.5，也就是K_T/K_S＞2）

 

远程的战斗：瞄准火力和兰彻斯特平方律

 

尽管希腊战场主要是重步兵的舞台，双方军队还是会拥有一些轻装部队（通常来说是非希腊籍的雇佣兵），他们被称为轻装步兵，（peltasts，此文文中可理解为远程步兵）。他们携带标枪和投石索，在战斗中向敌人投掷射击。轻步兵主要用于袭扰敌人两翼，除了几个非常特殊的战例之外，他们对战局不起决定作用。同样，我们让斯巴达的500名轻步兵与底比斯1000名轻步兵交锋，看看会发生什么。

 

在这种场合下，我们用到的模型是兰切斯特瞄准火力模型。斯巴达轻步兵P(t)及底比斯轻步兵Q(t)的变化率可以表示为：
 

 

这是因为标枪手间的战斗不再是一对一了。相反地，所有士兵可以在同一时间向敌人射击。（译者注：这里的“一对一”不是强调是否是两个人的单打独斗，而是指同一时间能够向敌人攻击的人数，在前面（1）、（2）方程的耦合系统中，某一时刻在进攻敌人的人数为定值N，（5）、（6）方程中这个值是此时刻尚存的人数。这也就是线性律和平方律的本质区别所在。）因此，P的死亡率等于向他们射击的Q的数值乘以一个系数α。同样，这里的变量α_Q不一定为常数，通常来讲在非瞄准射击的情况下，它是与P（即Q可以攻击的目标数）成正比的。简单起见，我们依然认为这两个参数为常数。

 

将（5）式除以（6）式，得到
 

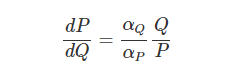
通过分离变量法解微分方程，并带入初始条件，得到
 

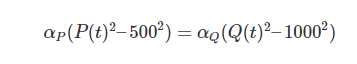
人数与总战斗力由线性关系变成了平方关系，这就是著名的兰彻斯特平方律。从这个等式中我们可以看出，数量要比质量更重要。比敌方人数少一半的斯巴达轻步兵的战斗效率要达到敌方的四倍(α_P/α_Q＞4)才能与其打成平手。这些等式是在1916年第一次世界大战时推导出的，或许可以解释当时的人们对军事的一些想法。

 

战斗当天
 

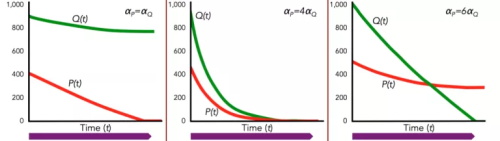
部队：这是战斗中的一个传统，因为士兵的左手绑着盾牌，前进中他们会有向右偏移的趋势，将精锐部队放在右翼可以遏制这种趋势。埃帕米侬达将自己的精锐部队放在左翼，这样以来他可以尽快消灭斯巴达军队的精锐，以免拖到后期己方在人数上的劣势会成为大问题。

 

 

吃完早餐并享用了一点葡萄酒之后，克莱奥姆波洛图斯国王和他的军队来到了留克特拉的开阔平地。国王和他最勇猛的战士位于右翼。可以看到远处的底比斯人正在缓缓接近，扬起一阵尘土。遭遇战首先在两军的轻步兵之间展开，此时两军的重步兵间还有一段距离。随着底比斯军队的靠近，克莱奥姆波洛图斯国王发现不对劲：底比斯人不按套路出牌，在斯巴达军队的右翼方向聚集了一个50排的队列。这50排队列冲到了克莱奥姆波洛图斯国王所在的位置。开始并没什么作用：残酷的战斗是在前排进行的，正如兰彻斯特线性律，双方都死伤惨重。然而随着战斗的进行，很显然50人纵深的底比斯军队不可能被仅仅12排的斯巴达人打败。目睹了斯巴达精锐部队一点点消亡并最终溃散，斯巴达的友军也开始效仿，竞相逃离战场，尽管在此时他们面对的敌人数还是比己方少的。和很多斯巴达士兵一样，克莱奥姆波洛图斯国王也被杀死了，斯巴达在希腊的统治地位画上了一个血腥的句号。

 

 

对模型的一点说明

 

兰彻斯特方程是人口种群建模中非常简单的一个例子，在对很多其他‘捕食者-猎物相互作用系统（其中最经典的要算是狐狸和兔子）’的建模中也有类似的方程。当然完全不必局限于两个“物种”，“物种”也不一定非要为有生命的有机体。

这些方程看上去太简单了，以至于他们并不能真正反映战争的形态。其中最突出的弱点就是兰彻斯特杀伤率。把一支军队的能力简化为一个不依赖于时间和空间的常数，这个假设真的很难被人认可。况且，该模型还要求两方军队都是同类的（也就是说所有部队在计算中都要被认为是一致的）。同时，这也反映了埃帕米侬达的精明之处：他并不把敌人简单地看作清一色的9600名重步兵，而是看作一小队斯巴达人加上一大堆没什么大用的盟友。依靠“擒贼先擒王”的策略，埃帕米侬达在军队人数上的劣势就不是什么问题了。正如J-K Anderson所说：“战场上双方军队中相当大的一部分和观众没什么区别”。

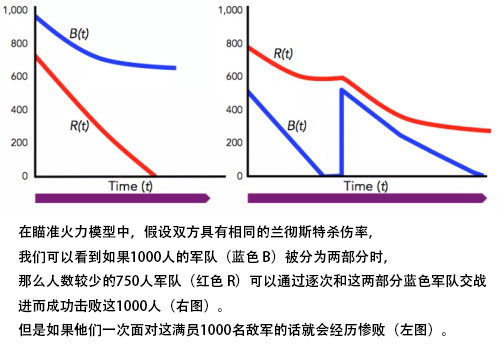
尽管这个模型有着缺陷，但是平方律揭示了瞄准火力模型比一对一模型更加有趣的特性。在瞄准火力的攻击情况下，将人数较多的军队分为两部分，让人数较少的军队逐次和这两部分军队交战，那么人数较少的军队也会取得胜利。这种战术会在线性律的模型下失效：如果斯巴达的盟友并未逃离战场，那么历史可能会被重新书写！
 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa