话说，在网上玩直播的是不是都应该感谢他？

 

原文作者，Jamie Condliffe。

翻译作者，ALIMJAN，哆嗒数学网翻译组成员。

校对，donkeycn。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

这就是傅里叶变换。你得感激它，因为帮你每天从网上下载音乐的、把图片压缩成很小的JPG文件的、甚至提高耳机消除噪声能力的都是它。下面介绍一下它的原理。

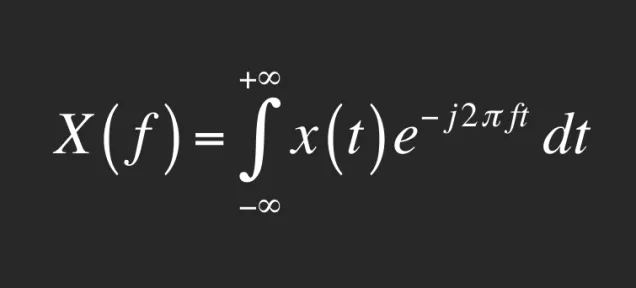
此公式的威力在于它能够使数学家快速掌握任何一种信号的频谱。这一点是相当牛的。但别以为只有我是这么认为的，早在1867年，物理学家开尔文勋爵也表达过自己对傅里叶分析爱慕至极。他写道：“傅里叶定理不仅是现代分析学里的最美的结论之一，而且也许可以说它充当了几乎破解任何晦涩的物理奥秘的必不可少的工具。”而且，至今仍是如此。

 

数学会将把我们分解

 

毫无疑问，傅里叶变换是数学家让·巴普蒂斯·约瑟夫·傅里叶男爵（Baron Jean Baptiste Joseph Fourier，1768-1830）创立的，并发表于他1822年出版的《热的解析理论》一书中。他对热如何在物体内部及其附近流动感兴趣，并在研究此现象的过程中推导出了傅里叶变换。当初，他自己并没意识到他的发现是何等重要的贡献——傅里叶变换不仅在数学和物理领域，而且在整个科学，工程和技术领域都是重要的发现。

 

他的主要突破性结果在于他意识到复杂的信号可以简单地表示为一系列简单得多的信号的叠加。他选择用来叠加的正是你在高中学到的、在最大值与最小值之间来回震荡的、规律可预测的正弦曲线。比如，当你同时按下钢琴的三个键时，你会产生三种不同的音符，其中每个都有确定的频率——我们在谈声音的时候指的是音高——这恰似标准的正弦波：

 

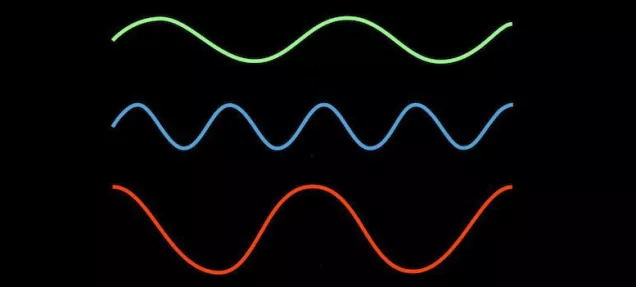
然而，一旦把它们叠加起来以后，原来那悦耳的和弦音听起来就比较杂乱，就像这个：

 

 

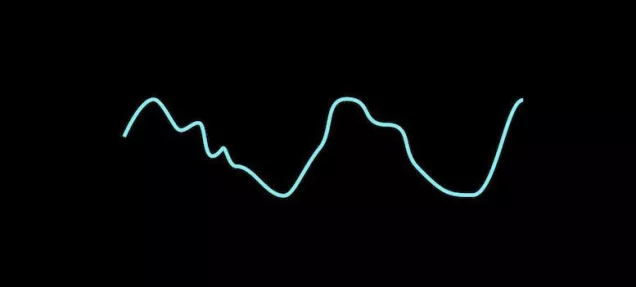
它看起来很复杂，但是我们知道本质上它只是同时把三个普通的正弦波叠加在一起。傅里叶的灵感在于他发现：无论一种波的最终形式有多么复杂，都可以用正弦波的组合叠加来描述——哪怕这意味着这可能需要使用无穷多个正弦波。我觉得这个发现的真正高明之处在于：若你知道为了得到最终的波形来代表信号，你需要知道叠加哪些正弦波，那么你也就可以精确地知道你需要叠加哪些频率的波以及每个波相应的特性。凭借这些知识，你就能精确地知道你叠加出来的最终的信号的频谱。

 

这些是本篇刚开始介绍的那个公式一下子就能做的事情。x(t) 这一项代表你想通过简单的信号的叠加来表示的那个最初的棘手复杂的信号，e^j2πft这一项看起来有点吓人，但是它只是数学家们用来代表我们以上说的正弦曲线的一个简略表达方式。绝妙的是，把这两项相乘然后整体扔进一个积分运算——前面的那个弯曲的符号以及后面的dt——这个运算能算出每一个参与组成最终信号必需的所有正弦曲线的频率。因此，公式的值X(f)，可以得出每一个需要参与叠加的简单分信号的强度和延迟。

 

这就是傅里叶变换：它的作用是能精确地揭示原始信号包含着哪些频率。这也许听起来微不足道，然而并不是。

 

传输

 

如果你要把你录制的歌放在网上，你可以只是按本来录制的原始大小的文件放上去，但那样的话，文件实在是太大了。这是因为，录制过程是个全程无损的：每一个频率在录制、混音至最后完成都会被保留。然而，如果拿一小段音频用傅里叶变换，你就会发现其中某些频率是很显著的而某些频率几乎不存在。

 

MP3格式的文件就是运用这个原理，只是它通过抛弃那些我们难以察觉的、或者是超出我们听觉范围上限的频率成分来节约空间，因为我们终归还是无法辨别出它们。整个过程都是如此，即把一首歌分割成上百万个小段，分离出重要的而抛弃那些无关紧要的频率。最终剩下的都是能够给在耳朵精准的播放出原音频效果的那些最重要的频率或音符。当然了，其文件大小要小于原来的十分之一。

 

这也跟Spotify的桌面客户端采用的Ogg Vorbis 格式的工作原理非常相似。（实际上，Vorbis采用的是傅里叶变换的快速计算版本：离散余弦变换，但其本质大略相同。）顺便说一下，Shazam也是运用类似的原理，它有着一个拥有不同歌曲频谱的数据库用于与你正在播放的歌曲的频谱比对，因为这要比直接比对两首歌曲要更可靠。就音频而言，你所戴的降噪耳机同样也是依靠傅里叶变换：有一个麦克风会记录你周围的噪音，得出其全部频谱，然后叠加与这些噪音相同频率、但位相相反的波到你的音乐中从而将类似于婴儿哭声或马路噪声之类的噪音清除。

 

当然傅里叶公式并非只有这一个技能。我们目前只谈到音频这种时间信号，当初傅里叶创立它是为了解决物体之间的热流问题。这表明，傅里叶公式也可以用来处理关于空间的问题。对于傅里叶而言，这意味着在二维平面内通过叠加一些简单的热流来表示复杂得多的热流。以十分相似的方式，傅里叶变换也可以比一个像素一个像素的处理方式更有效地来创建数字图像。

 

无损的彩色图像文件的每一个像素都有它独特的颜色。当你以JPG格式存一个图片时，整个图片被分割成许多小块，并且在每个小块都进行二维傅里叶变换。它提供了在每一小块上颜色和亮度如何变化的空间频率的描述。类似于处理MP3格式的文件那样，JPG抛弃了一些能使图像画质更高的高频的成分。然而，对于大部分人来说，人眼毕竟区分不出相近的颜色之间的一些微妙差异，因此抛弃那些高频部分后所导致的一个像素一个像素的变化，人眼几乎是看不出来的。显然，你如果继续压缩，开始抛弃越来越低频的成分时，图片会出现块效应，即在块与块的边界处颜色的变化会很明显。

 

除了那些拥有最训练有素的眼睛、耳朵的那些人，在多数情况下，类似MP3,JPG等的压缩文件是几乎不可察觉出和压缩前有何区别的。它们看起来、听起来都特别逼真而且占用空间比它们那些无损的版本来说是微不足道的。换言之，压缩让数字音乐和数字图像变得可行，使得我们更容易地分享。这一切都是一个公式的绝对惊人的妙处。毋庸置疑，写了热流理论书的傅里叶会赞成的。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa