【大结局】数学上下三万年(八):二十世纪下半叶的数学
原文作者,圣安德鲁斯大学数学与统计学院。
翻译作者,mathyrl,哆嗒数学网翻译组成员。
校对,math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
从今天起,我们将连载这部数学编年史。本文是翻译版本,因为工作量巨大,必有疏漏(包括原文也会有错误),欢迎指正。
这应该是网上最全的数学编年史,从公元前30000年到公元2000年,哆嗒数学网为你奉献。
这里是 【大结局】数学上下三万年(八):二十世纪下半叶的数学
二战结束,和平与发展成为世界主题。计算机的广泛使用让世界逐步进入信息时代。
本期出场人物有:塞尔、霍奇、柯尔莫哥洛夫、米尔诺、斯梅尔、索伯列夫、邦别里、科恩、格罗腾迪克、阿蒂亚、森重文、康威、瑟斯顿、曼德博、唐纳森、孔涅、怀尔斯、威腾、朗兰兹等。
中国人或华人也有陈景润、丘成桐、王秋冬登场。
本系列下面是往期内容:
1950年
卡尔纳普(Carnap)出版了《概率的逻辑基础》(Logical Foundations of Probability)。
1950年
汉明(Hamming)发表了关于误差检测与误差校正编码的基础论文。
1950年
霍奇(Hodge)提出了关于射影代数簇的“霍奇猜想”。
1951年
塞尔(Serre)利用谱序列来研究纤维丛的纤维、全空间和底空间的同调群的关系。这使得他发现了空间的同调群与同伦群之间的基本关联,并证明了球面同伦群的重要结果。
1952年
霍尔曼德尔(Hörmander)开始了偏微分方程理论的工作。十年后他因为这项工作获得菲尔兹奖。
1954年
塞尔(Serre)由于他的谱序列的工作以及层的复变理论的工作获得了菲尔兹奖。
1954年
柯尔莫哥洛夫发表了关于动力系统的第二篇论文。这标志着KAM-理论的开始,这个理论的名字来源于柯尔莫哥洛夫(Kolmogorov)、阿诺尔德(Arnold)与莫泽(Moser)。
1955年
嘉当(Cartan)与艾伦伯格(Eilenberg)发展了同调代数,将强大的代数方法与拓扑方法关联起来。
1955年
诺维科夫(Novikov)证明了群的字问题不可解。
1955年
谷山丰(Taniyama)提出了关于椭圆曲线的猜想,将在费马大定理的证明中起到重要作用。
1956年
米尔诺(Milnor)出版了《论同胚于7维球面的流形》(On manifolds homeomorphic to the 7-sphere),打开了微分拓扑的新领域。
1957年
柯尔莫哥洛夫解决了“希尔伯特第13问题”,它是关于某些3变量连续函数不能被表为2变量连续函数的问题。
1958年
托姆(Thom)由于拓扑学的工作获得菲尔兹奖,特别是有关示性类、配边理论和”托姆横截理论”。
1959年
布恩(Boone)证明了群的许多判定问题不可解。
1959年
马歇尔·赫尔(Marshall Hall)出版了他的著名教科书《群论》(Theory of Groups)。
1960年
铃木通夫(Michio Suzuki)发现了有限单群的新的无穷族。
1961年
爱德华·洛仑兹(Edward Lorenz)发现了一个具有混沌现象的简单数学系统。它导致了被广泛应用的混沌理论的新数学。
1961年
斯梅尔(Smale)证明了n > 4的高维庞加莱猜想,即同伦等价于n维球面的n维闭流形必定是n维球面。
1962年
雅各布森(Jacobson)出版了他的经典教科书《李代数》(Lie algebras)。
1962年
索伯列夫(Sobolev)出版了《泛函分析在数学物理的应用》(Applications of Functional Analysis in Mathematical Physics)。
1963年
约翰·汤普森(John Thompson)与费特(Feit)发表了《奇数阶群的可解性》(Solvability of Groups of Odd Order),证明了所有非阿贝尔有限单群都是偶数阶群。他们的论文用了250页来证明这个定理。
1963年
科恩(Cohen)证明了选择公理与连续统假设的独立性。
1964年
广中平佑(Hironaka)解决了代数簇上有关奇点消解的一个重要问题。
1965年
谢尔盖·彼得罗维奇·诺维科夫(Sergi Novikov)关于微分拓扑的工作,特别是计算稳定同伦群与分类光滑单连通流形,导致他作出“诺维科夫猜想”。
1965年
邦别里(Bombieri)利用他改进的大筛法证明了关于算术级数的素数分布的“邦别里中值定理”。
1965年
杜奇(Tukey)与库利(Cooley)发表了一篇论文,介绍了快速傅立叶变换算法。
1965年
塞尔顿(Selten)发表了区分在预测博弈结果时的合理决策与不合理决策的重要工作。它导致了1994年的诺贝尔奖。
1966年
格罗腾迪克(Grothendieck)由于他在几何、数论、拓扑与复分析的工作厄尔获得了菲尔兹奖。他的概型理论使得韦伊的几个数论猜想得以解决。他的拓子理论与数理逻辑高度相关,他给出了黎曼-罗赫定理的代数证明,并给出了曲线基本群的代数定义。

1966年
兰德尔(Lander)与帕金(Parkin)利用计算机寻找欧拉猜想的反例。他们找到了27^5 + 84^5 + 110^5 + 133^5 = 144^5。
1966年
艾伦·贝克(Alan Baker)证明了“格尔丰德猜想”,它是关于有理数域上代数数的线性独立性。
1967年
阿蒂亚(Atiyah)发表了《K理论》(K-theory),详述了他关于K理论的工作和指标定理,而之前此工作让他获得了1966年的菲尔兹奖。
1968年
诺维科夫(Novikov)与阿迪安(Adian)联合发表了一个证明,证明了对于d > 1与n > 4380,伯恩赛德群B(d, n)是无限的。
1969年
康威(Conway)发表了他的新的零散有限单群的发现。
1970年
艾伦·贝克(Alan Baker)由于他在丢番图方程的工作获得菲尔兹奖。
1970年
马季亚谢维奇(Matiyasevich)证明了“希尔伯特第10问题”不可解,即没有通用方法判定一个多项式方程是否有整数解。
1971年
史蒂芬·库克(Stephen Cook)提出了有关多项式时间算法的P vs NP问题。
1972年
托姆(Thom)发表了《结构稳定性与形态发生学》(Structural Stability and Morphogenesis),解释了突变理论。这个理论研究了渐变力导致突变的情况,在光学与生物学有重要应用。
1972年
奎伦(Quillen)阐述了高阶代数K理论,它是一个新工具,使用几何与拓扑的方法与思想来描述与解决代数中的重要问题,特别是环论与模论。
1973年
德林(Deligne)证明了三个“韦伊猜想”。
1973年
陈景润证明了每个充分大的偶数可表为一个素数与一个不超过两个素数的乘积之和。它是对哥德巴赫猜想的重要贡献。

1974年
芒福德(Mumford)由于代数簇的工作获得菲尔兹奖。
1975年
费根鲍姆(Feigenbaum)发现了一个新的常数,约等于4.669201609102...,它涉及倍周期分岔,在混沌理论中起着重要作用。
1975年
曼德博(Mandelbrot)出版了《分形学:形态,概率和维度》(Les objets fractals, forme, hasard et dimension),描述了分形理论。
1976年,拉卡托什(Lakatos)的著作《证明与反驳》(Proofs and Refutations)在他去世两年后发表。首次在1963-64年分4部分发表,这部著作给出了拉卡托什关于数学如何发展的阐述。
1976年
瑟斯顿(Thurston)由于他在叶状结构(Foliations)的工作获得美国数学会韦伯伦几何学奖。
1976年
阿佩尔(Appel)与哈肯(Haken)使用1200小时的计算机时间检验了大约1500个构型证明了四色定理为真。
1977年
阿德曼(Adleman)、李维斯特(Rivest)和萨莫尔(Shamir)引入了公钥编码,它是一个用于传递秘密消息的系统,使用大素数和一个公开密钥。
1978年
费夫曼(Fefferman)由于他在偏微分方程、傅立叶分析,特别是收敛性、乘数算子、发散性、奇异积分与“哈代空间”的工作获得菲尔兹奖。
1978年
森重文(Mori)证明了“哈茨霍恩猜想”,即射影空间是具有丰富切丛的唯一光滑完备代数簇。
1979年
孔涅(Connes)出版了关于非交换积分理论的著作。
1980年
有限单群的分类完成。
1982年
曼德博(Mandelbrot)出版了《自然的分形几何》(The fractal geometry of nature),比1975年的工作更完整地发展了他的分形几何理论。
1982年
弗里德曼(Freedman)证明了同伦等价于4维球面的4维闭流形必定是4维球面。这是在1961年斯梅尔的工作之后证明了高维庞加莱猜想的进一步情形。
1982年
丘成桐(Shing-Tung Yau)由于他对偏微分方程、代数几何中的卡拉比猜想、广义相对论的正质量猜想以及实与复蒙日-安培方程的贡献获得菲尔兹奖。

1983年
唐纳森(Donaldson)出版了《自对偶连接与光滑4维流形的拓扑》(Self-dual connections and the topology of smooth 4-manifolds),导致了关于4维流形几何的全新思想。
1983年
法尔廷斯(Faltings)证明了“莫德尔猜想”。他证明了对任意充分大的n,最多有有限组互素的x,y,z满足x^n + y^n = z^n ,这对费马大定理作出重要贡献。
1984年
布兰吉(Louis de Brange)解决了比贝伯猜想。
1984年
沃恩·琼斯(Vaughan Jones)发现了3维球面中纽结和链的一个新多项式不变量。
1984年
威腾(Witten)出版了《超对称与莫尔斯理论》(Supersymmetry and Morse theory),包含了在微分几何研究中具有核心重要性的思想。
1986年
马古利斯(Margulis)证明了关于不定无理二次型在整点的值的“奥本海默猜想”。
1987年
泽尔曼诺夫(Zelmanov)证明了关于一个无穷维李代数何时为幂零的重要猜想。
1988年
朗兰兹(Langlands)是第一个获得美国国家科学院数学奖的人。他获奖是由于“将群表示论带入到与自守形式理论和数论的革命性新关系的非凡远见”。
1988年
艾尔基斯(Elkies)找到了欧拉猜想在n=4的一个反例,即2682440^4 + 15365639^4 + 18796760^4 = 20615673^4.。其后同年弗莱斯(Frye)找到了一个最小反例:95800^4 + 217519^4 + 414560^4 = 422481^4。
1989年
布尔甘(Bourgain)使用分析与概率方法解决了L(p)问题,这是在巴拿赫空间理论与调和分析中为时已久的问题。
1990年
德林菲尔德(Drinfeld)由于在量子群以及数论的工作在日本京都的国际数学家大会获得了菲尔兹奖。
1991年
泽尔曼诺夫(Zelmanov)解决了群论的有限制的伯恩赛德问题。
1991年
王秋冬(Quidong Wang)找到了n体问题的无穷级数解(除了少量例外)。
1993年
梅纳斯科(Menasco)与斯莱维(Thistlethwaite)证明了纽结理论的猜想“泰特第二猜想”,即同一个素纽结的两个约化交错图由一个扭转序列关联。
1994年
怀尔斯(Wiles)证明了费马大定理。
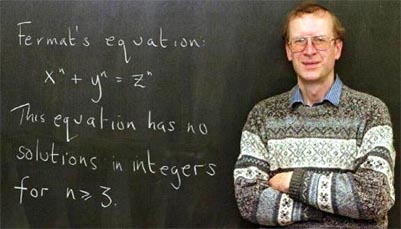
1994年
孔涅(Connes)出版了关于非交换几何的重要教科书。
1994年
利翁(Lions)由于他在非线性偏微分方程的工作获得菲尔兹奖。
1994年
约克斯(Yoccoz)由于他在动力系统的工作获得菲尔兹奖。
1994年
克里斯蒂娜·古皮尔堡(Krystyna Kuperberg)解决了关于动力系统拓扑的“塞夫特猜想”。
1995年
银行家安德鲁·比尔提供大奖悬赏求解比尔猜想:对p, q, r > 2以及互素整数x, y, z,方程x^p + y^q = z^r 无解。
1997年
怀尔斯由于解决了费马大定理获得沃尔夫斯凯尔奖。
1998年
博赫兹(Borcherds)由于在自守形式与数学物理的工作获得菲尔兹奖;高尔斯(Gowers)由于泛函分析与组合数学的工作获奖;孔采维奇(Kontsevich)由于代数几何、代数拓扑与数学物理的工作获奖;麦克马伦(McMullen)由于全纯动力系统与3维流形几何的工作获奖。
1998年
托马斯·黑尔斯(Thomas Hales)证明了关于最密堆积的开普勒问题。
1999年
互联网梅森素数大搜索项目(GIMPS)找到第38个梅森素数:2^6972593 -1。
1999年
康拉德(Conrad)与泰勒(Taylor)证明了“谷山-志村猜想”。怀尔斯在1993年解决费马大定理的途中证明了其中一个特殊情形。
2000年
在洛杉矶举行的美国数学会的一个会议上提出了“21世纪的数学挑战”。不同于100年前的“希尔伯特问题”,这次的问题由30位数学家的团队给出,其中8位是菲尔兹奖得主。
2000年
一个700万美元的大奖被设立来求解七个著名数学难题。称为千禧年大奖难题:P vs NP;霍奇猜想;庞家莱猜想;黎曼假设;杨-米尔斯规范场的存在性与质量缺口;纳维-斯托克斯方程解的存在性与光滑性;贝赫和斯维纳通-戴尔猜想。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

评论已关闭