在数学或者物理中，什么是“事情被证明了”！

 

原文作者，AskaMathematician网站。

翻译作者，radium，哆嗒数学网翻译组成员。

校对，Math001。

 

注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

最初的问题是：......让我感到困惑的是一些像巴拿赫-塔斯基悖论（又称“分球怪论”）以及其他在纯数学和理论物理中抽象的概念，都可以认为是已经“被证明”的。那岂不是违反了在真实/物理世界中只能通过实验来验证假设，从而证明某件事情的原则？ 即使如此，说任何事情都可以毫无疑问地证明是不是有点不太合理？

 

物理学家：假设检验是科学探究的主力，用于决定假设成立可能性的大小。假设检验的结果不是承认，也不是否认的结果。是一个估计你会不小心看到给定结果的可能性。发生意外的可能性越小，它就越有可能成为真正的影响。 例如，我们还没有证明希格斯玻色子存在，只是因为CERN的数据偶然会产生一兆分之一的概率。 这不是一个证明。 即便如此，如果一个现象按照预测的方式运行，那么你也可以相信它是真实的。

 

事情“被证明”是确实可靠的，就像我们可以肯定地知道有人赢得了一场国际象棋比赛一样。 宇宙结构中没有任何东西可以决定棋子在棋盘上移动的方式（除了自然的变化）或谁赢了某场比赛，然而每个了解这些规则的人都可以成为胜利者。而数学，基本上就和国际象棋或其他游戏的规则差不多(虽然看似自己玩自己的，但它是最纯粹的科学，它以最简单的思想让我们摆脱对事物模糊的把控）。

 

一旦规则被建立，你就可以基于这些规则和一些逻辑证明一些事情（技术上讲，逻辑只是更多的规则）。例如，基于直接了当数学规则的合理简短列表，您可以首先定义素数是什么，然后证明它们的数量是无限的。

 

数学中的规则被称为“公理”而基于这些规则的结果被称为“定理”。例如，“你不能将一个点分成两半”这是一个公理，与此同时“有无限多的质数”是一个定理。当你第一次了解到数论和算法时，你会学到皮亚诺公理（Peano's axioms）以及基很多定义和基于这些定义的结论。就像下棋的规则一样，公理规定了在数学中你能做和不能做的事，从中人们可以自由地去探究他们可以或不可以得到的结论。数学没必要让得到的结论都来自于实际，因此它恰好包括了一些利用最有效的工具去理解它所构造的事物。

 

事实上，我们没有根据实际生活创造的数学似乎看起来没有价值，但结果常常是这些数学却变得相当的有用。例如，通过将几何学的规律从三角形，三维空间甚至距离概念中推广出来，数学家为爱因斯坦的广义相对论铺平了道路（它描述了在扭曲时空方面引力的性质）。基本上，他仅仅是把他关于时空的想法用数学上早就创造出的结论表达了出来。

 

 

巴拿赫塔尔斯基分球悖论在集合论中已经存在了一个世纪之久了。他说的是你可以（除了其他因素外）把一个球分成五个或更多的集合，旋转然后移动一些集合，然后重新组合它们可以得到和最初一样大小的两个球。这些集合不像块拼图碎片，更像雾中的水滴，几乎所有的这些集合都小于给定尺寸。值得注意的是，这些在现实生活中是完全不可能的。分球怪论托了数学的福，它不被现实的严格限制所主宰。

 

巴拿赫塔尔斯基分球悖论基于集合论中一般的公理，策梅罗-弗兰克尔（Zermelo–Fraenkel，简称ZF），但是需要增加一个具有争议的公理，即“选择公理”（ZFC）。在数学界，“具有争议”的是似乎有点用词不当；数学家们大多时候都在自顾自的写长篇论文，如果需要打断写作而交流，他们只会悻悻地相互打量一下。选择的公理对于数学，就像吃过路兵对于国际象棋一样，当它被需要时，它就出现了，但是你一般不需要它（设想你曾经在下国际象棋时被人吃了过路兵，但你并不知道具体它是什么）。

 

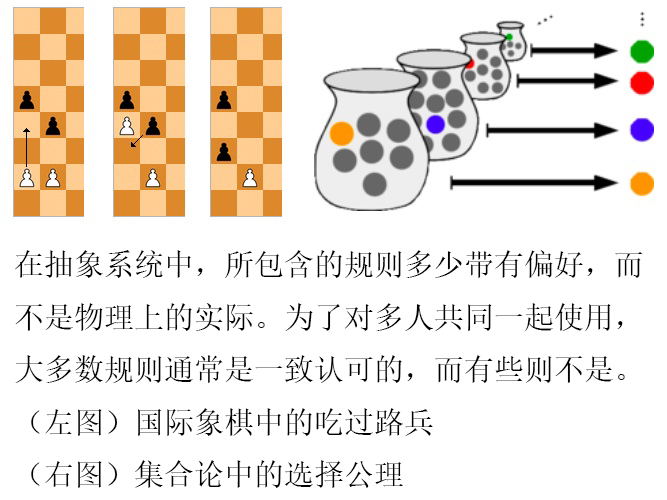
选择公理说的是你总是可以从无限多个集合中在每个集合里取出一个元素。如果集合只有有限个这是显然的（“放手去做就行了”），或者你可以提出一个合适的规则将这样的元素取出来（例如“每个集合中取最小的数”）。但是有时你会遇到无限个集合中的无限个元素。没有最大、最小甚至中间的元素。如果你想知道如何从这些集合中挑选一个唯一的元素，选择的公理说“大哥，稳，你可以的”。这是被提出来改变游戏规则的一个完整的陈述。这不是真的或假的问题，而是数学家与其他数学家之间一致统一以及和睦相处的问题。

 

物理学，尽管是科学的女王，我们凡人可以努力理解现实本质的手段，也不比数学好。在物理学中，你可以“证明”事物会发生或不会发生，但仅仅是基于已建立的规则：“物理定律”。例如牛顿万有引力定律说，两个相距为r，质量分别为M和m的物体间的吸引力为F=GMm/r²。不仅仅是一个事实的陈述，像这样的数学表达式允许我们精确地描述或预测事物的物理行为。根据这个定律（和其他一些）我们可以精确地证明轨道是椭圆的。注意到“精确”，但不一定是“真的”。

 

如果这些规则被实验证明是错误的，那么基于它们的证明不是真正的证明。这就是为什么物理学家如此小心地建立和验证他们的理论的每一个细节。他们花费了（似乎浪费了）几十年的时间来测试他们已经几乎100%确定的东西。因为任何基本定律的缺陷都会波及到基于它的每一个“被证明”的事物。

 

数学或物理学中的一些基本规则或假设被颠覆了。在数学中，这完全是由于逻辑，但是物理要求得更多。我们不能仅仅用逻辑来推测宇宙的规则。如果你只是用头脑空想，这个宇宙的本质将是对你一个真正的冲击。无论你有多聪明，你都需要实验和观察来了解关于世界的新事物。

 

很容易（是的.......很容易）写下一些物理规律，这些规律似乎描述了我们对宇宙的了解，但结果却是错误的。 如果没有大量精确的数据和数学来支撑它，就没有办法知道你知道的东西仅仅只是你的想法。牛顿定律是非常有用的，但最终被证明和现实也不是完全贴合的。他们根据我们当时的数据完美地描述了宇宙；当更准确（更难以获得）的数据产生“更真实”的物理理论时，我们开始意识到牛顿的物理学是仅仅只是非常好的近似值。

 

在爱因斯坦之前，我们已经习以为常地认为时间和空间是完全独立的。它采取了一些严肃的深奥的现象（例如，光速的不变性和水星轨道上的微小误差），表明时间和空间是相互关联的，它们是同一事物的不同方面。在贝尔之前，人们几乎完全笃信，无论我们是否知道这个状态是什么样的，认为一切都是在一个明确的状态下进行的，这个看似完全合理的假设就是“现实主义”。

 

同样，我们认为的宇宙和我们目前触及到的宇宙的差异（可能）是一组不可思议的深奥的、几乎不可察觉的效应（例如，放射性衰变和纠缠粒子的“不可能”统计数据的随机性）。这些效应花了很多精确的实验去验证（尽职检查，阐述，并多次验证）以及利用数学得出结论：不，一个如此基本的假设，我们称之为“现实主义”或“现实假设”实际上是错误的。量子物理学家已经超越了通常的理解，他们将这个性质定义为“单一状态”的“反事实确定性”（counterfactual definiteness）。这没什么好说的，但是如果你能看懂，你很厉害。很好。

 

在数学中，虽然你可以证明一些东西，但是最终就像棋局，你仅仅只是在棋盘上移动棋子。在逻辑领域里有很多东西需要理解和发现，但是数学，和所有人类的抽象思考一样，全都存在于我们的头脑中。

 

在物理学中，你不仅可以用物理定律来证明事物，而且那些物理定律是唯一真实的，因为它们总是在每一个场景中完美成立（我们可以测量和验证），就是说，你可以放心的相信他们。

 

注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa