当你喝醉走路时，你知道你找到了圆周率吗？

原文作者：RHETT ALLAIN，东南路易斯安娜大学物理副教授。

翻译作者，radium，哆嗒数学网翻译组成员。

校对，Math001。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

宛如来到一个不曾发现的海域，最妙的事情莫过于你可以通过一种新的方式找到圆周率的值，比如说，醉汉走路式的随机游走。那么问题来了，什么是随机游走？好问题！我现在就来告诉你。

你站在某个位置上开始走动。最简单的情况就是从x=0这个位置上开始。如同抛掷一枚硬币，正面？漂亮，我们向右移动一个单位。反面？也行，我们就向左移动一个单位。只要你开心，重复这个过程，那么恭喜你，你实现了一维上的随机游走。通常的，我倾向于画一个图来解释这个过程，但是今天我将用python中的随机游走代码来替代它。来看这个代码。

n=0

ball=sphere(pos=vector(0,0,0), radius=0.1, color=color.yellow)
attach_trail(ball)

start=sphere(pos=vector(0,0,0), radius=0.2, color=color.red)

while n<100:
  rate(5)
  temp=random()
  
  if temp<0.5:
    ball.pos.x=ball.pos.x+1
  
  else:
    ball.pos.x=ball.pos.x-1
  n=n+1
ball.color=color.cyan
ball.radius=0.2
start.radius=0.2

练习代码将帮助你理解具体的过程，但我也将伪代码展现出来了。

从0到1中提取随机数
如果数字小于0.5，向x轴的正方向移动
如果数字大于0.5，向x轴的负方向移动
重复这个过程，直到你百无聊赖为止

但是随机游走一步就太没意思了，在次数较多的情况下又会发生什么情况呢？现在设置重复100步，当然，我一次性跑完，我将在-100到100之间的任何地方。但是如果我将这100步运行1000次，我就可以计算出平均情况下我会落在哪个地方。这个直方图展示了一维情况下，1000次100步的随机游走：

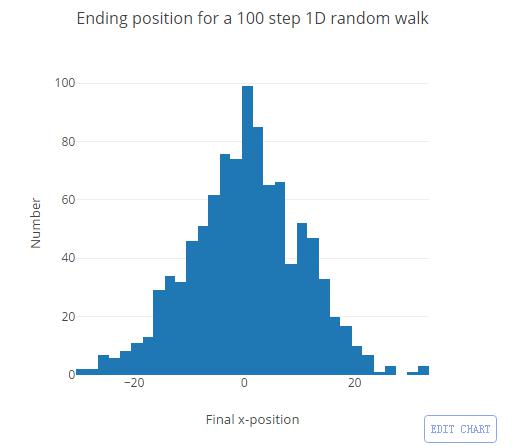
这样我就找到了一个点来描述平均位置，但为什么要这么麻烦呢？似乎很显然终点位置的平均值就在原点啊。可以理解，如果每一次我都是一相同的概率不是向左走就是向右走，很多次之后，那么我向左走的步数等于向右走的步数，好像也是，我会回到原点。

那么我们画一个从原点到终止点的总距离的图像又会怎样呢？x轴的值是取的是位移的绝对值，和从开始到结束的总距离一样。

 

 

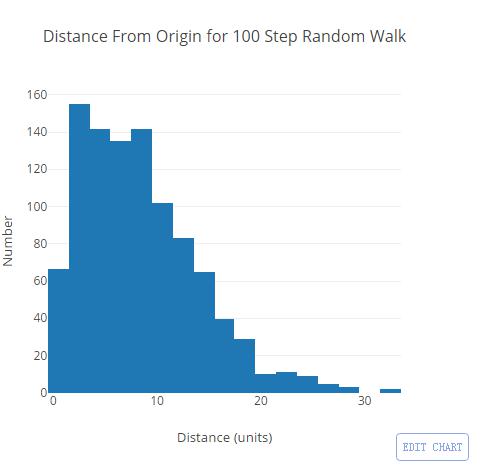
是的，事实上，这看起来很疯狂，平均的距离（不是位置）是7.848而不是0.但这也是合理的，如果你看第一个直方图，x的最终位置出现次数最多的是在x=0这个点上。但是x=-1和x=1的总次数超过了x=0上的值，而且也是取的正值，这两件事便导致了非零的平均位移。

好吧，为了不让你等太久，那我们就一起去寻找π。所以我将给你一些“派”因为我通常在π节吃派（开个玩笑，我经常在π节写π才是正道）。当然，你已经意识到随机游走的平均位移由步数所决定，恩，是这样的，但对吗？但是它将证明平均位移也由π决定。我们给出关系如下（祈求你不要叫我推导它）：

 

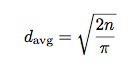
在这个表达式中，n是步数，从中，我们可以用随机游走去寻找pi的值。“A计划”如下：一次随机游走10步（做1000次，取平均值）。重复这个过程，再一次随机游走20步，30步，以及更多。如果你画一个平均位移平方关于步数的关系图，你可以得到一条斜率为2/π的直线：

 

 

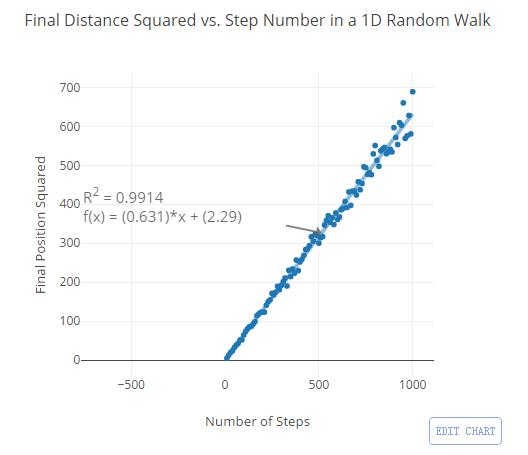
这里的斜率为0.631，因为它等于2/pi，所以我们可以得到pi值为3.1696.不太精确（π=3.1415....）,但对我来说已经足够接近了。这意味着，你可以在那个区域内做一条直线去更好的估计pi。你可以通过改变每一次游走的步数去估计。当你在程序中输入更多的步数（例如1000步），嗯，我可能应该输入更多的步数，因为这样更精确。啊哦，好吧你可以去胡搞瞎搞一下。

二维的随机游走

 

也许这就是爱情吧，我被随机游走深深的迷住了。但总在我快要失去控制时，有人把我拉回来了。在这期间我也做了一个二维的随机游走。就像一维的随机游走一样，这时，我的每一步就有4种选择—+x, -x, +y, -y。对的，这仍然是一个离散的随机游走（一个格子状的随机游走），每一步都只有一个单位，因此我也只在坐标轴上的整数值位置。

这就是我可视化的二维随机游走100步的代码，只要你开心，你可以随意修改它。

n=0
ball=sphere(pos=vector(0,0,0), radius=0.1, color=color.yellow)
attach_trail(ball)
start=sphere(pos=vector(0,0,0), radius=0.3, color=color.red)
while n<100:
  rate(25)
  temp=random()

  if temp<0.25:
    ball.pos.x=ball.pos.x+1
  elif (temp>=0.25 and temp<0.5):
    ball.pos.x=ball.pos.x-1
  elif (temp>=0.5 and temp<0.75):
    ball.pos.y=ball.pos.y+1
  else:
    ball.pos.y=ball.pos.y-1

  
  
  n=n+1
ball.color=color.cyan
ball.radius=0.5
start.radius=0.5

为了更“好看”，我改变了两个小球的大小和颜色，代表随机游走开始和结束的位置。看着“醉汉”在哪里乱窜，好吧，好玩吧!来,让我们来看一些有用的干货。我随机游走100步，重复1000次，平均位移会是多少呢？你期待的直方图如下：

 

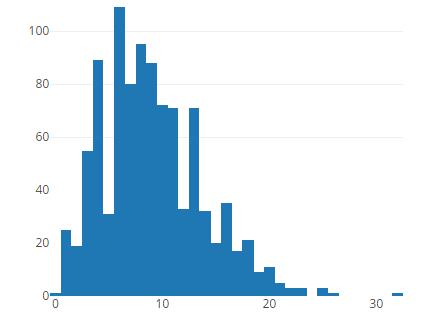
直方图告诉我们平均位移为8.820个单位。也许这不是太坏的结果，就像之前的一维随机游走一样，你可以找出平均位移和步数之间的关系：

 

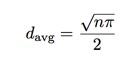
见证奇迹的时刻，我再一次绘出了平均位移的平方和步数之间在关系图，在这一个例子中，斜率为π除4.

 

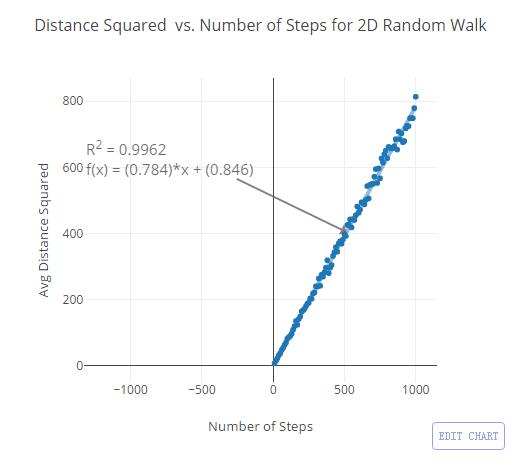
从数据中的到的斜率，我们得到了π的值为3.136，哇哦，不太差。但这仍不是最好的方法，但很有趣哦~

 

让我们再随机游走一次

 

我保证这是最后一次随机游走了，至少在这篇帖子上是这样。这次游走仍然在二维，但有一点不同，哪有“醉汉”只在x轴或y轴方向上移动的啊？我们让每一步都成一个随机的角度进行游走。这就意味着我的走动不一定停在一个整数点上。

n=0
ball=sphere(pos=vector(0,0,0), radius=0.1, color=color.yellow)
attach_trail(ball)
start=sphere(pos=vector(0,0,0), radius=0.3, color=color.red)
while n<100:
  rate(25)
  temp=random()

 theta=temp*2*pi
 dr=vector(cos(theta), sin(theta),0)
 ball.pos=ball.pos+dr  

  n=n+1
ball.color=color.cyan
ball.radius=0.5
start.radius=0.5

这对距离的寻找会出问题吗？我们依旧来看距离平方关于步数的图：

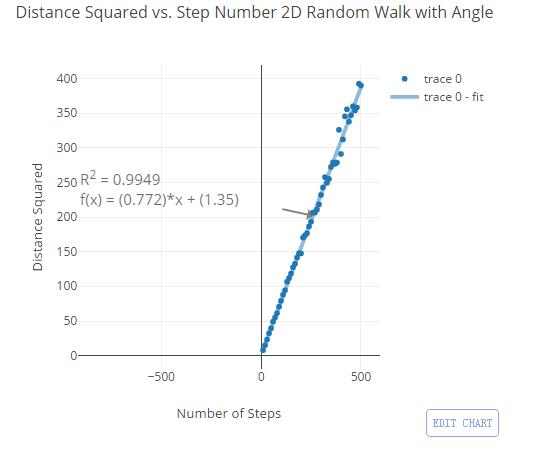
看吧，这就是我们想要的结果。这就是π，就像一位隐藏在现实世界背后的日本忍者，它会突然出现在你没料到的地方。

 

家庭作业

 

你不做点关于π的家庭作业吗？

看看是否会得到一个更好的距离平方关于步数的图。尝试多一点的步数，或许没那么多噪音。
如果你创立一个方向和每一步的大小都是随机的二维的随机游走过程，看看会发生什么？我承认这有点艰苦，因为你不能用均匀随机数（均匀分布的随机函数），除非你来决定每一步的范围。你可以限定每一步的范围从0到1，然后用高斯分布去决定每一步的大小。
尝试用三维的离散随机游走去寻找π。小技巧:你可以寻找三维中距离和步数。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa