万物皆数:被上帝选中的幸运儿皆是数学世界中的一种计算方式
长久以来,“随机”的问题就令人着迷。从史前时代起,原始人就观察到了一系列不能够解释、不符合常理的现象,这些现象没有什么明显的原因,纯粹是来自大自然的“馈赠”。在最初,人们找不到什么更好的解释,于是他们归咎于神灵。日食、彩虹、地震、瘟疫、洪水或者彗星都被视为来自上天的神圣消息,只有那些能够与上天“对话”的“专业人士”才能解读。于是,这个任务往往被交给巫师、神使、祭司或者其他的萨满,这些人会在大众面前做一场全套的仪式(这就是他们谋生的手段),用来质问神灵,因为他们不再想等待让这些随机事件自己出现。换句话说,古代的人们已经开始想方设法地自己创造出“随机”效果。
“孛罗芒西”(La bélomancie),或者称之为“箭卜术”,就是非常古老的例子之一。对于想要问神的问题,将可能的各种答案写在箭身之上,然后把这些箭放在箭筒之中,摇晃箭筒并且随机抽取出一根:这就是神的回答。举例来说,公元前6世纪,古巴比伦国王尼布甲尼撒二世就是用这种方法选择他的敌人,进而发动战争。除了箭之外,人们用来抽签的物品简直多种多样:小石头、黏土片、小木棍或者彩色球。古罗马人给这些物品起了个名字叫“离者”(sors),法语中“抽签”(tirer au sort)一词的字面意思就是“抽出离者”。类似的还有“ 巫术”(sortilège)一词,这个词的原意有两个?质问神灵或者来自神灵的审判。
慢慢地,“抽签随机”的机制流传开来,在很多的应用中都能发现它们的身影。一些政治系统曾经使用过它们,比如在古代的雅典,人们用这种方法选出参加众议院五百人会议的市民,又比如,在几个世纪之后的威尼斯,人们把这种方法用在了总督任命的程序之中。“随机”同样也是游戏创作者们的重要灵感来源。人们利用它发明了猜硬币正反面游戏、带编号的色子(当然还借助了柏拉图立体的外形),甚至卡牌游戏。
正是这种能够“传递神的旨意”的随机游戏,最终吸引了一些数学家的注意力。这些数学家开始有了“玩儿转命运测量器”的奇怪想法,通过逻辑和运算,他们研究了未来将会发生的事情的概率。
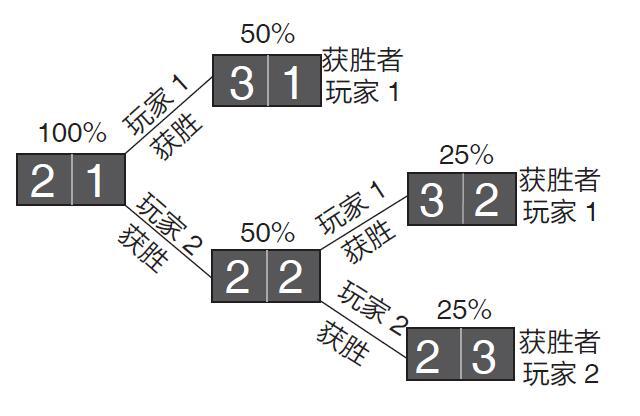
所有这一切都始于17 世纪中叶巴黎科学会?博向所有与会者提出了一个他自己构思的问题。他说,试想一下,有两个玩家在玩儿随机游戏并且押了钱,先赢得3局者胜出,当玩儿到2∶1的时候,游戏被中断了,试问这两位玩家该如何分割赌桌上的赌注?
在当日与会的所有科学家中,有两个法国学者对这个问题产生了特别的兴趣,他们是皮埃尔·德·费马和布莱兹·帕斯卡。在几封书信往来之后,这两位学者最终得出的结论是,第一位玩家应该获得四分之三的赌注,第二位玩家应该获得四分之一的赌注。
为了得出这一结论,两位学者演绎了假设游戏没有被中断的、各种可能发生的场景,然后估算了玩家1和玩家2各自的获胜概率。于是,在假想的“下一轮”游戏中,玩家1有50%的概率获胜,而玩家2也有50%的概率获胜。在这种情况下,两位玩家就需要再来一轮,而这一轮当中,两位玩家的获胜概率依然是相等的,也就是说,两位玩家分别获胜的场景都有25%的概率会发生。所有关于这个游戏“未来”的可能走向,可以用下页的图表来表示。
总之,我们可以看到,在未来,玩家1有75%的概率获胜,而玩家2只有25%的概率获胜。于是,帕斯卡和费马一致认为,两者应该按照同样的比例分割赌注:玩家1拿75%,玩家2拿25%。
两位法国学者的推论过程可以说非常富有成效, 大部分博弈游戏( 概率游戏) 都能够用这种方法来检验。瑞士数学家雅各布· 伯努利是第一批紧跟帕斯卡和费马脚步的学者之一, 他在17 世纪尾声的时候撰写了《猜度术》(Ars Conjectandi )一书,这本书在1713 年伯努利死后出版。在这本书中,伯努利分析了经典博弈游戏,并且首度提出了概率论中的基本原则之一:大数定律。

这条定律确认了,在随机试验中,我们重复的次数越多,结果的平均值就越明显,并且趋近于一个极限值。换句话说,从长期来看,即使是最复杂的随机,最终都会产生一个平均行为,因此,所谓的“随机”也就不再存在了。
为了理解这个现象,我们倒是不必离题太远,只需要一个简单的“猜硬币正反面”游戏就能感受到大数定律的存在。假设我们投掷一枚硬币,正反面均匀,每一面都有50% 的概率朝上,可以用以下直方图来表示。

现在,假设你连续投掷硬币两次,并且记录正面和背面朝上的次数。有三种可能:两次都是反面,或者两次都是正面,或者一次正面一次反面。人们很容易认为这三种情况发生的概率是相同的,但事实却并非如此。实际上,出现一正一反的可能性为50%,而出现两次正面或者两次反面的概率都只有25%。
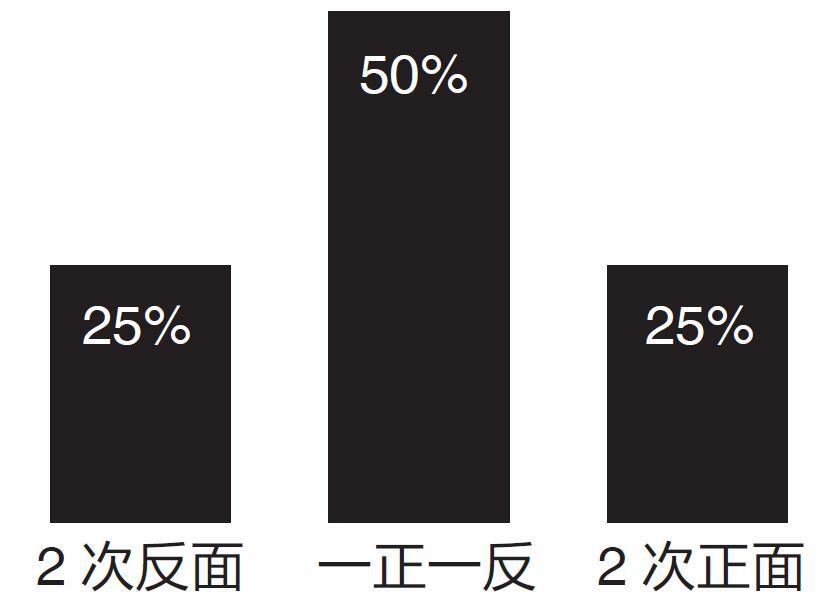
这种“不平衡”的结果,实际上是由于“两次不同的随机过程可能产生同样的最终结果”所导致的。当我们连续投掷两次硬币的时候,实际上会产生以下四种情况:反―反,反―正,正―反和正―正。反―正和正―反两种情况产生的是同一种结果,即一正一反,这就解释了为什么一正一反出现的概率是其他情况的两倍。类似地,玩家们都会知道,如果我们同时投掷两枚色子,它们的点数和等于7 的概率要远远高于等于12 的概率,因为等于7 的情况有很多种(1 + 6,2 + 5,3 + 4,4 + 3,5 + 2 和6 + 1),而等于12 的情况只有一种(6 + 6)。
我们投掷的次数越多,这个现象就越明显。最初出现机会均等的那些场景逐渐地产生区隔,一些成了极少数,一些成了普遍情况。如果你连续投掷10 次硬币, 会有大约66%的概率得到4 ~ 6 次反面;如果你连续投掷100 次硬币,有96% 的概率会得到40 ~ 60 次反面; 如果你连续投掷1000次硬币, 有99.999 999 98% 的概率会得到400 ~ 600 次反面。
如果我们分别画出投掷10 次、100 次和1000 次的直方图, 就可以看到,逐渐地,绝大多数“未来的可能”围绕着中心轴收紧,以至于那些对应着极端情况的矩形,我们的肉眼已经看不见了。
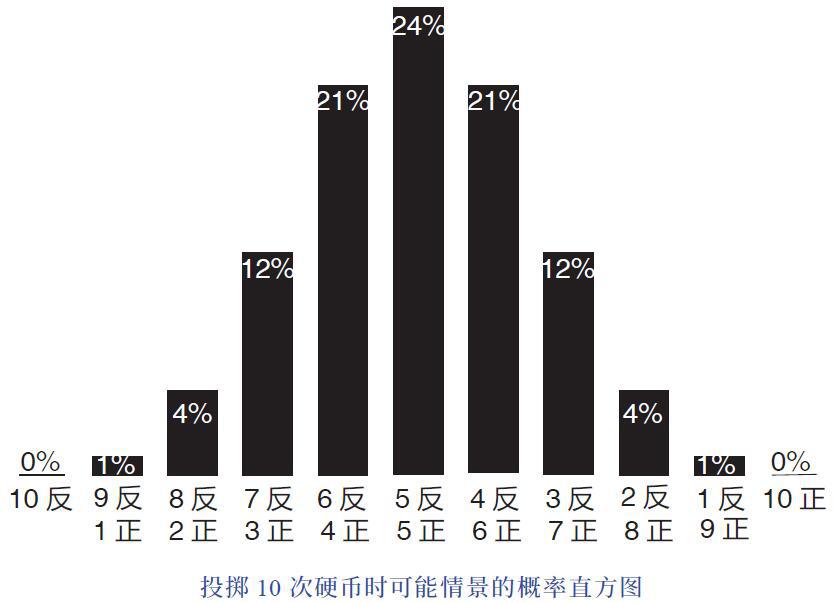
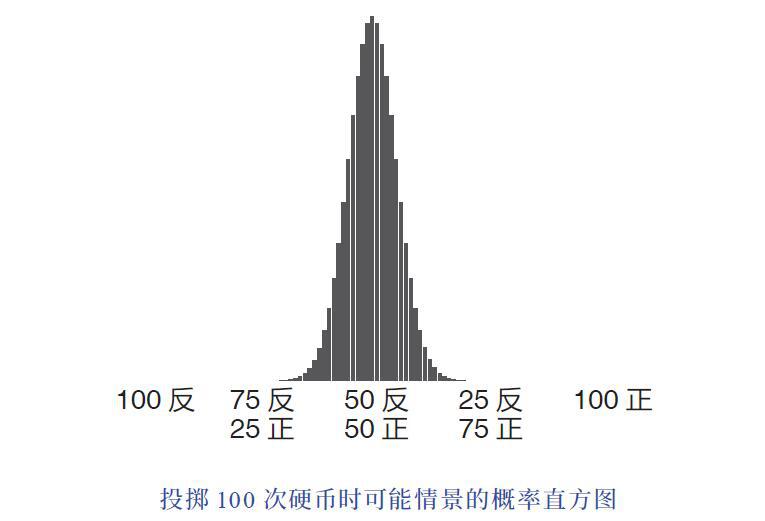
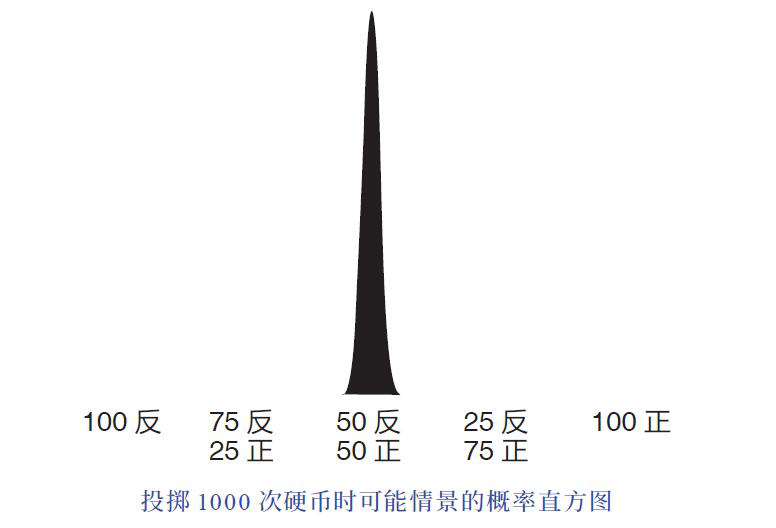
总之,正如大数定律所断言的那样:无限次地重复某个随机试验,最终的平均结果必然不再是随机的,而是无限接近一个极限值。
这一原则是测验调查和其他数据统计的操作基础。在某一人群中,选择1000 人,问他们更喜欢黑巧克力还是牛奶巧克力。如果600 人回答黑巧克力,400 人回答牛奶巧克力,则很有可能在整个群体中?哪怕这个群体总数有几百万人?比例仍然是一样的,60% 的人喜欢黑巧克力,40% 的人喜欢牛奶巧克力。调查某个随机抽取的人的口味可以被认为是一个和扔硬币猜正反面游戏相同的随机实验,只是我们的选项从正面和反面换成了黑巧克力和牛奶巧克力。
当然了,我们可能运气不好,正好抽到了1000 个人全都更喜欢黑巧克力,或者1000 个人全都更喜欢牛奶巧克力。但是这种极端情况发生的概率也是极端小的,因为大数定律向我们保证了,只要随机抽取的样本足够大,所获得的结果就有非常大的可能会接近整个人口的平均值。
进一步考察多种场景和它们在未来可能发生的概率,我们还可以建立一个置信区间,并且评估错误的风险。比如,我们可以说,有95%的可能会出现如下情况,即这个人群中喜欢黑巧克力的人数比例在57%~63%之间。实际上,任何缜密的调查研究都应该总是能获得这些可以显示其精确度和可靠性的数字。
评论已关闭