什么都是数学？搞个蛋啊！

 

原文作者：John D Cook。

翻译作者，独行者，哆嗒数学网翻译组成员。

校对，Math001。

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

你将如何用公式描述一个蛋的形状呢？这里告诉你蛋的一个方程如下：

 

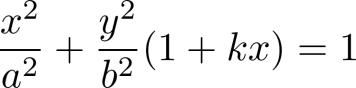
我们会发现，如果k=0，我们便会得到一个椭圆。k越大，越不对称于y轴。

我们在Mathematica上验证一遍：

代码

    ContourPlot[
        x^2/16 + y^2 (1 + 0.1 x)/4 == 1, 
        {x, -4, 4}, {y, -3, 3}
    ]

 

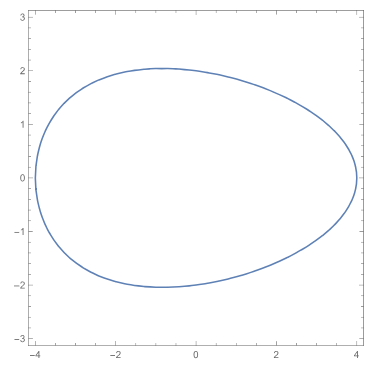
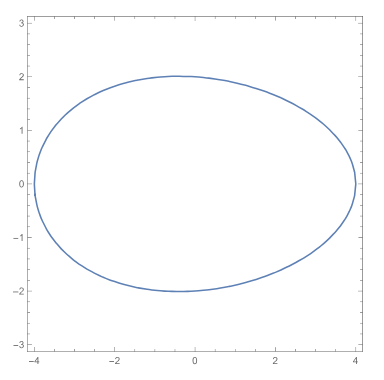
我们让k=0.05，这样看上去更像是一个椭圆。

对参数的研究

如果要对一个鸡蛋进行详尽的描述，你该如何确定a, b, k的值呢？

令y=0，则2a是鸡蛋的长度。令x=0，则2b是鸡蛋在中心的宽度。需要注意的是，这不是鸡蛋的最高位置，因为最高处在中心的左侧。（如果k是正数，则在左边。k可以为负数，这样最高处则会翻转到y轴的右边）。

我们通过确定最高处x的值来表示k。

我们有以下方程

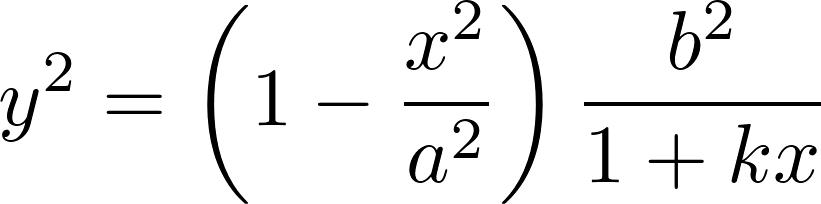
隐函数求导可知

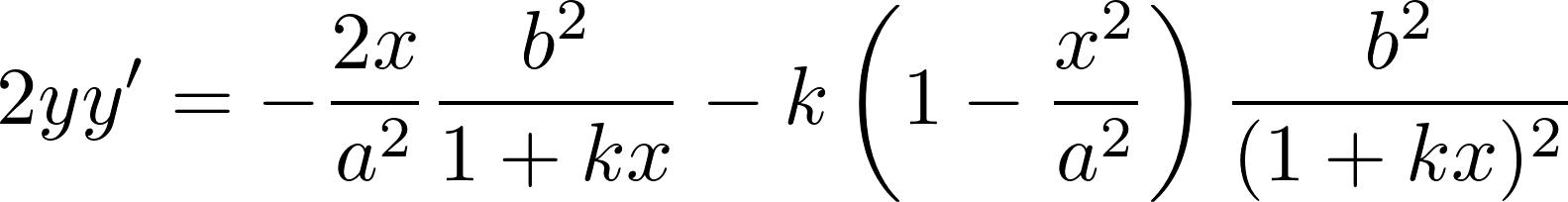
在最高处y的导数为0， 所以等式右边也应该为0。于是我们便知道了k的值。

 

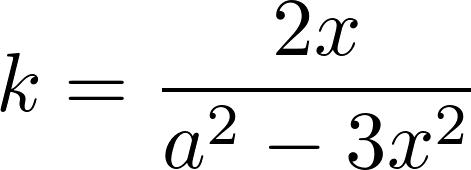
曲率

k值越大，鸡蛋便会在左边变的越平整，右边则会越尖。我们会对鸡蛋两端的变化进行量化分析。

由隐函数F(x,y)=0确定的曲线，曲率可以由以下式子算出

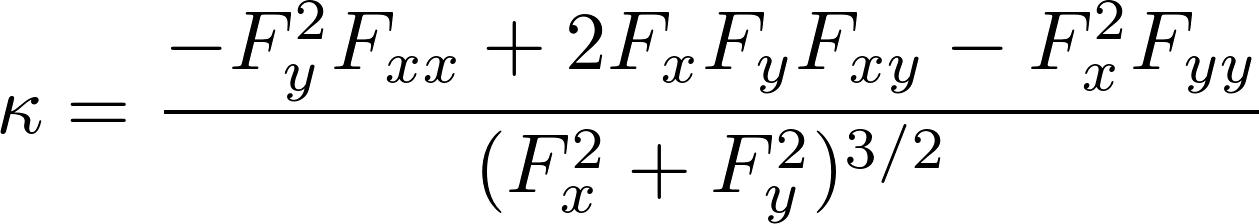
上面的等式在我们关注的(±a, 0)两个点上可以化简掉很多参数。

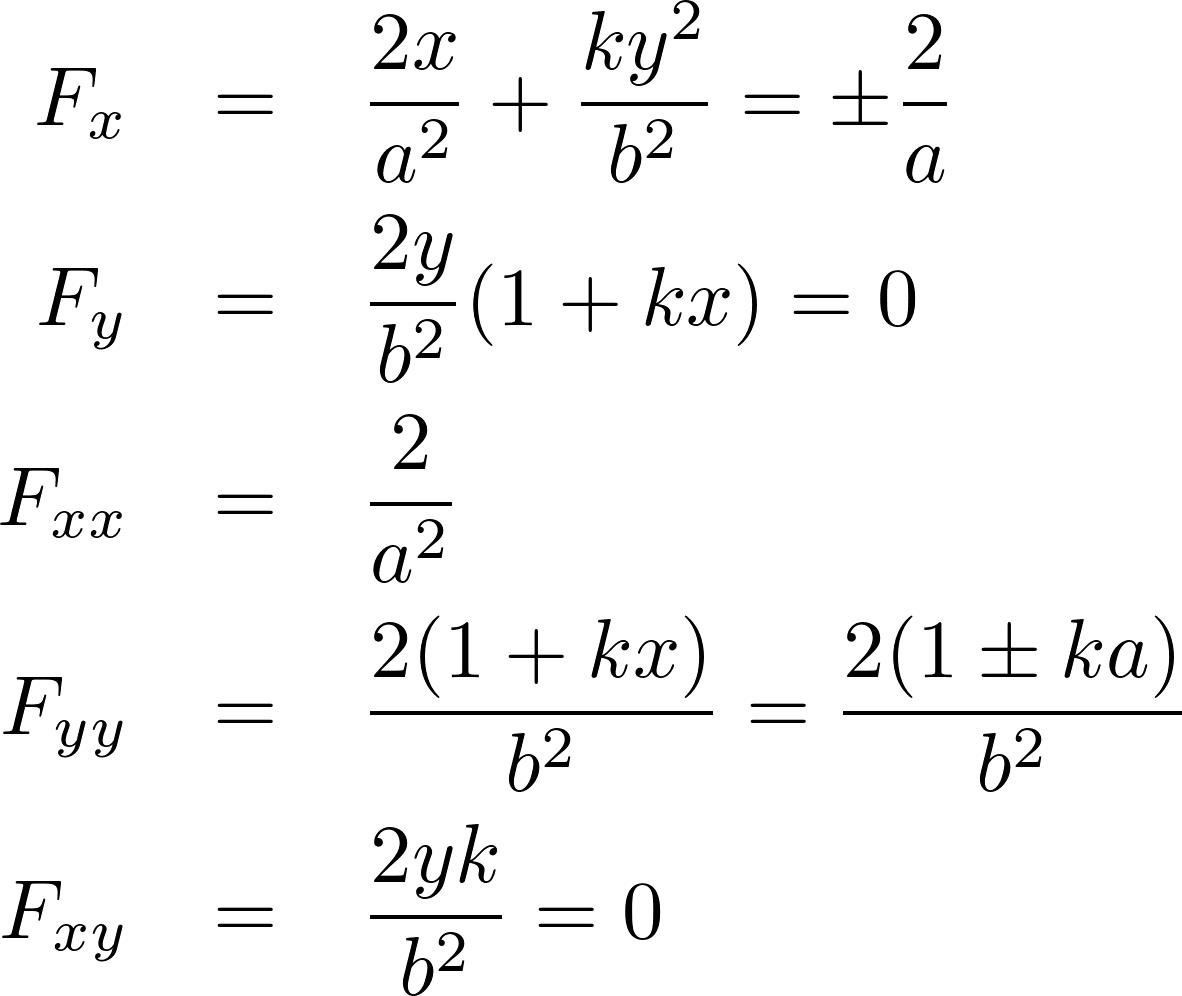
于是，曲率简化成：

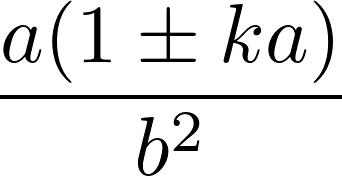
因此，在我们一开始给出的例子当中，当a=4，b=2和k=0.1时，左边的曲率为0.6，右侧的曲率为1.4。第二个例子，k=0.05，则左侧曲率为0.8，右侧曲率为1.2。

同样是这两个例子，那么如何计算鸡蛋的体积呢？

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa