真的吗？阿蒂亚爵士声明证明100万美元的黎曼猜想！

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

菲尔兹奖和阿贝尔奖双料得主阿蒂亚爵士（Sir Atiyah）日前声明证明了久负盛名的黎曼猜想。并将在9月24日在海德堡获奖者论坛上发表这个演讲。从目前论坛官网披露的信息来看，证明方法是一个全新的方法，但并不复杂(simple proof)。这次的证明基于之前冯诺依曼、希策布鲁赫、狄拉克的工作。

 

 

黎曼猜想是数学界最重要的猜想之一(有人说可以把“之一”两字去掉)。克雷数学研究所现在还悬赏100万美元征解。问题本身，只需要有过复变函数学习经历的人都能看懂。而它的一个等价变形，高中生都能看懂。

 

黎曼猜想原始版本

 

考虑下面一个函数项级数定义复变函数，

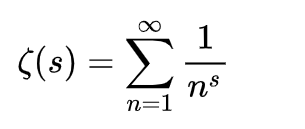
在实部Re(s)>1时，级数收敛，其余部分(s≠1)可以用解析延拓得到。解析延拓后的函数，叫做黎曼ζ函数。经过，一些简单的计算，对于负偶数，ζ(-2n)=0，那么负偶数就是黎曼ζ函数的平凡零点。而黎曼ζ函数还有别的零点，叫做非平凡零点。目前，发现的黎曼ζ函数的非平凡零点是的实部都是1/2。于是，黎曼猜想是说黎曼ζ函数的所有非平凡零点的实部都是1/2 。

 

高中生能看懂的版本

 

我们先来定义这样两个函数。

对于一个正整数n，我们把它所有的约数加起来，得到的正整数记为σ(n)。比如24的约数为1,2,3,4,6,8,12,24，那么σ(24) = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60。 

同样是正整数n，我们把不大于它的所有正整数的倒数加起来，记为H(n), 就是说H(n)=1 + 1/2 + 1/3 + ... + 1/n . 比如H(3)= 1 + 1/2 + 1/3 = 11/6 。 

通过σ(n)和H(n)，黎曼猜想等价于下面这个不等式成立：

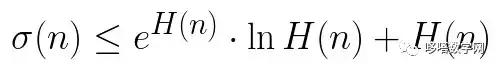
是否是“真”证明还得等待

 

不过，声明要得到确认，需要同行专家审稿通过。数学界内，之前也有声明证明某个大猜想，最后发现证明错误的情况。就阿蒂亚爵士本人，之前也有“劣迹”，2016年他声明证明了六维球面S6上无复结构但没有了后文。

至于这次是真是假，作为吃瓜群众只能等待了。我们哆嗒数学网小编发稿时，海德堡获奖者论坛已经崩溃。

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa