数学家都喜欢解决最烧脑的问题？不！这位数学家不同！

原文作者，Kevin Hartnett，《量子》资深作者。

翻译作者，whymath，哆嗒数学网翻译组成员。

校对，333。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

背景

 

 

数学中大多数重要的发现要经过几十年或几个世纪的努力才能得到。如果你想要研究数学中最难的问题，就必须要掌握大量高专业性的知识，才能发表些新的看法。

 

数学家Richard Schwartz沉浸在他所发现的简单数学问题的奥秘中

 

而这些最难的问题没有引起理查德·施瓦茨(Richard Schwartz)的兴趣。他喜欢的那种可以今天读，明天着手解决的问题——简单的、有趣的、有些像游乐场游戏那种走一步看一步的问题。施瓦茨的这种性格在理论数学家中相当少见，他曾说：“我觉得自己对数学的态度是童真的”。

 

 

但这并不是说施瓦茨不是一个严肃和卓有成就的数学家。恰恰相反，他在近半个世纪来最重要的数学家之一——比尔·瑟斯顿(Bill Thurston)的指导下于普林斯顿大学获得了博士学位，现在他是布朗大学的终身教授，并在动力系统领域取得了他最重要的研究成果——研究迭代过程的长期表现，如一个台球在无摩擦桌面的跳动现象。2008年，他证明了每个内角都小于100度的三角形任意都包含至少一条台球路径——一个台球将在其上做周期性往返运动的路径（注: 想象在一个无摩擦的桌面击打一个台球，这样台球将不断碰到桌壁，然后反弹。假如过了几年再回来看，会发现什么？施瓦茨证明了这个台球将以行星绕太阳旋转般的方式在固定的轨道上做周期运动，而非不断产生新的路径）。

 

 

施瓦茨在其多数工作中都使用了计算机实验，可称得上是这方面的弄潮儿。正他说，计算机在好些方面对人类的数学思维形成了助力：计算机找到的模式给予了证明问题的启示，而这是很难单靠人脑想到的。

 

 

《量子》杂志对施瓦茨进行了访谈，访谈内容包括其本人对简单问题（他称之为“数学奇迹”）的喜好和他即将面世的关于无穷的儿童数学读物。以下是整理过的谈话内容。

 

 

您喜欢数学的什么？

 

 

我喜欢关于它的全部。当然了，我首要喜欢的是它有用。我喜欢它是流程化的这个事实，这让你总可以找到前进的方法。我喜欢它不像政治和宗教，在这些领域内的讨论多少年都不能改变对方的观点，而数学则可以探入到问题的最深处。

 

 

我还喜欢几何图形和数字，我对他们有着我所无法解释的原始的热爱。还有我也喜欢智力挑战，我喜欢解决问题，尤其是大家无法解决的那种——这有些像登山者的心理。最后，我还喜欢纯数学的美，就像有人喜欢艺术品一样。

 

 

您说您喜欢简单的问题，为什么？

 

 

 

我觉得如果一个简单的问题还没有被解决，那么这个问题一定还有隐藏的深度，即存在人们所意想不到的事情阻碍了问题的解决。

 

 

其次，我还喜欢做计算机实验，因此我时常感到我有在这种问题上取得进展的机会。现代计算机是一个新的工具，而这些简单问题也可以被视为数据(模式)搜索的渠道。比如，我正打算在计算机上编程并做一些实验，来发现那些隐藏的模式，以前这些模式没有被人发现，就是因为没有人做过这样的实验。

 

第三，我所喜欢的简单问题不需要太深的背景知识，可能听起来有些傻气，我喜欢那种我恰好可以介入的那种问题。我还很有耐心，如果听说一些流行数学领域的猜想，我不会予以理会，我不喜欢花上六个月的时间读文章，然后才能达到着手解决问题的地步。我喜欢接地气的，可以立刻开始的那种问题。

 

 

什么是简单问题？举个例字？

 

 

我非常感兴趣的问题之一就是三角台球问题。它是这样说的：观察一个三角形内的台球，是否存在一条周期性的台球路径，使得台球在这条路径上一遍又一遍的重复其运动轨迹？对锐角三角形来说答案是已知的，但对钝角三角形来说则不然。问题是：对于任意三角形来说，都存在这样的周期性台球路径么？我在这个问题上做了一些努力，证明了若三角形的内角均小于100度，则该路径存在。

 

 

可以请您再举一个例子么？

 

另一个我曾下了一些功夫才解决的是外台球问题。假设你有一个平面上的凸形，椭圆，正方形或五边形都可以。然后你就从凸形外一点，嗯，也许我该画个图来说明。

 

 

 

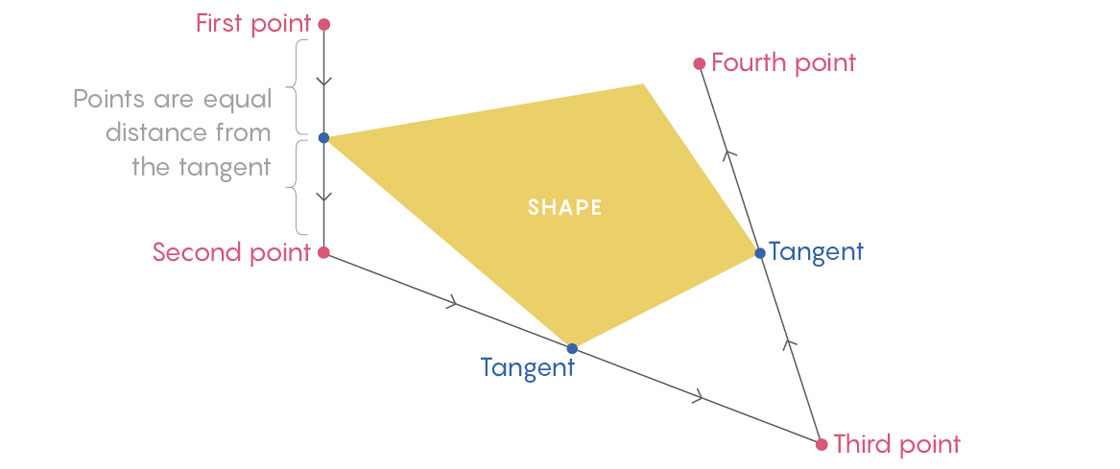
从凸形外的某个起始点（第一个点）开始，做凸形的一条切线（与凸形仅有一个交点的线），然后在离切点距离等于切点至起始点距离的地方停下来，这是第二个点。重复这个过程，最后由这些移动的点形成类似星体轨道的图形。

 

核心的问题就是：是否存在这样的凸形和起始点使得动点可任意的远离凸形？动点的运行轨道是否是无界的？我证明了对于某些特定的凸形，比如风筝，这种具有双侧对称性的四边形，动点将远离凸形。

 

 

请告诉我您是怎样在工作中使用计算机的，以及为什么您喜欢使用？

 

我首先要说的是，计算机是用来打草稿的利器。数学家，甚至伟大如高斯和欧拉，都曾致力于搜索实验证据。他们将在草稿纸上手算问题的特殊情况为自己提供关于结果的灵感。在某种意义上，你可以用电脑做很多类似的事，它让你搜索更多的关于可能的正确结果的实验证据。

 

朱利亚集可以显示为表示某个复杂函数行为的分形

 

计算机还是一种可视化的工具。它揭示了这样一件事：没有它的帮助你可能将无法得出正确的观点。一个真的要用到计算机的好例子是曼德布洛特集，不使用计算机，你当然可以徒手绘制出一系列的散点，而一旦使用计算机进行辅助，却能够揭示蕴含其中的丰富信息。没有大量的计算和绘图，曼德布洛特集，朱利亚集以及类似的事物将是不可能被看见的。

 

存在计算机解决不同本质的问题的方式么？

 

我只能说我个人认为，数学十分适用于高对称性的事物。从某种意义上说，数学几乎是奇迹。一个近期的大型的例子是玛丽娜·维娅佐夫斯卡(Maryna Viazovska)在八维空间给出的开普勒猜想（这个猜想就是球体最密堆积问题）的解。令人惊讶的是，开普勒猜想的解决在八维空间内要比在三维空间内容易得多。原因是这些神奇的球堆积在八维空间是极其、极其对称的，在八维空间内这样特殊的构造简直就是神迹，但若没有这些非同寻常的对称，从某种意义上说，问题就无从下手了。所以计算机在这里帮了大忙，因为它使你能够对所有的可能性进行遍历。

 

 

您说数学被有组织的用于寻找那些最对称或最美丽的事物，可以请您详细谈谈么？

 

这就像是数学行经这个世界时，毫不犹豫地拾起了最闪耀最美丽的宝石。譬如对数函数、零函数、指数函数，几何中则是线和面，最近的流形学中则是曲率空间和概型一类的奇怪的东西——我不大能理解这些东西。数学就是用在这些典型事物上的。你可以说这才是数学家们应该做的——寻找更多的类似的典型，更多的宝石。但回过头来说，这可能是那种初看起来十分难的不起眼的宝石。

 

 

那么计算机可以帮助找到这些不起眼的宝石吗？

 

 

当然能了，那是我从外台球问题得到的经验。一开始，外台球在一个风筝形的平面上产生的运动看起来完全是噪声，而且很难理解，我不断尝试使用不同的方式来表示数据，最后我想到了画出更高维度的数据表示，突然，我的眼前就出现了这个美丽的模式。我敢说，没有计算机的帮助，我永远都猜不到这个答案。

 

 

计算机可以搜集大量的信息，可以将事物图形化，可以作为你的外部存储空间，因此它可以帮助你识别那些太渺远以至于无法识别出来的基础模式。计算机是一条捷径，你可以在太多的地方用到它了。某种程度上，你甚至不需要花脑子想问题，至少一开始不用，然而你同样将得到计算机的反馈，然后你再根据这些反馈调整实验。并且假如你成功了，一定将发现单靠自身所无法找到的新知识。

 

Schwartz家中书房的分形时钟

 

您写了好几本儿童数学读物，您写作这些书籍的动力是什么？

 

 

 

原因有两个。我孩子还小的时候，我想要教他们数学。一开始，我为我的女儿露西写了一本薄的关于素数的书，但后来我沉迷于这件事无法自拔，写成了一本叫做《快来数怪兽》的完整的书。我的孩子是我莫大的动力，因为我总想要向他们解释这些整洁的东西。另一个原因是我喜欢画画，我画的不算太好，但我就是喜欢计算机绘图。嗯，就是这样。

 

 

 

数学之外，我喜欢的有创造性的东西，它们是我日常研究之外的小憩，我喜欢拥有大量的观众。像大多数数学家，我致力于研究的问题——即使这些问题被解决并且构成了另一个未解决问题的解——不太可能有好几百人愿意了解。而知道自己的图画书被好几千人阅读则是一件很值得高兴的事。

 

 

 

在数学上我投入了大量的脑力工作，我想知道，如果我在一些问题上工作地十分努力，而得到的成果只有很少的人将会看到，那么生命的意义何在？也许，撰写这些儿童读物会是我知道自己的研究成果正以正确的方式发挥作用的机会。

 

 

你正在写一本新的儿童读物《无穷农场上的生活》，你打算向孩子们传达关于无穷的什么呢？

 

在孩提时代，我曾想了很多关于无穷的事——如果我有无穷长的胳膊会怎样，如果桌子是无穷的又会怎样。我认为孩子们会喜欢的，无穷是一个有趣的概念。

 

 

 

 

 

 

Schwartz的第四本上市书籍《无穷农场》中的示例页面

 

关于无穷，有什么特别想要孩子们理解的东西吗？

 

 

 

第一件事就真的是对无穷的感觉了，无穷并不是一件东西。比如古典音乐，假如你从未听过古典音乐，你可能会想古典音乐就是音乐，但假如你有兴趣了解的话，你会知道音乐其实是巴洛克、古典、浪漫、现代——所有风格和乐器的组合。这个例子主要是为了让孩子们了解无穷的可能性，因为音乐是事物走向无穷的另一种方式。

 

 

 

还有另外一个实质性的部分，就是要让孩子们看到一些让人眼前一亮的真正激励他们的东西。孩子们在学校的学习通常枯燥无味，尤其在数学方面。知识通常没有被很好的传授，孩子们也经常被填鸭式地教育，那样的方式毫无生趣。所以我的想法是传达一些孩子们真正感兴趣的激励他们的东西。

 

 

你从事数学工作的30年来，对数学的理解有过改变么？

 

我不知道，某种意义上来说，我对于数学的态度并没有改变多少。我对高端的流行的数学从不感冒，比如朗兰兹计划或范畴论，这一点我从未改变。我认为我对数学的态度是童真的。我记得我在母校的时候还曾这样想：好像身处某个游乐场，你看到有很多不同的游戏，比如向可乐瓶子扔环套住它之类的，你似乎只需要做些游戏就能拿到你的博士学位。我一直没有什么大的研究项目，我仍然痴迷于这些奇怪的简单问题。

 

 

也许现在我越来越熟知的一件事就是人类的知识充满了漏洞。关于数学，年轻无畏的你认为万事尽在掌握，而我却感觉所知不过沧海一粟。人们如首尾相衔的蚁群般不断前行，所经过的轨迹窄小得可怜，轨迹外的世界就是未知的世界，这就是我越来越强烈的明悟。

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa