蛋蛋的表面积

原文作者，John D. Cook博士。

翻译作者，独行者，哆嗒数学网翻译组成员。

校对：math001

 

关注 哆嗒数学网 每天获得更多数学趣文

 

我们之前的文章中，介绍了鸡蛋的一个拟合公式，讲解了公式中各个变量对鸡蛋形状和鸡蛋两端曲率的影响。

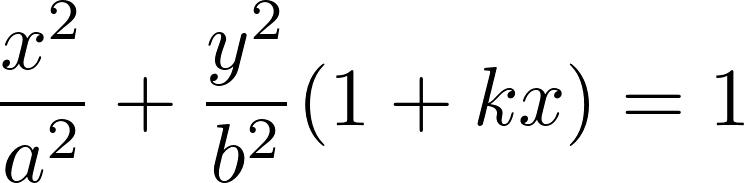
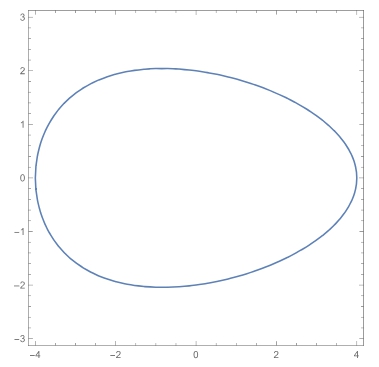
在那之后的文章中则介绍了鸡蛋的体积计算。而篇文章，我们将介绍鸡蛋的表面积计算。

 

如果你将f(x)在[c,d]之间的图像绕x轴旋转，那么这个立体图形的表面积为：

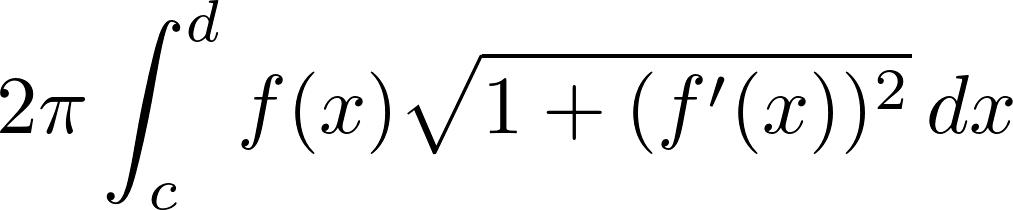
对于鸡蛋的拟合函数而言，这个积分是没有初等表达式的。（至少我没有找到初等表达式，就算用Mathematica也无能为力。）但是我们可以通过计算得到数值解。

 

下面给出的是Mathematica的代码。

f[x_, a_, b_, k_] := b Sqrt[(1 - x^2/a^2) / (1 + x k)]
area[a_, b_, k_] := 
    2 Pi* NIntegrate[ 
    f[x, a, b, k] Sqrt[1 + D[f[x, a, b, k], x]^2], 
    {x, -a, a}
]

 

现在我们进行更为详尽的考察，我们来验证一个观点，如果鸡蛋是球状的，我们会得到球的表面积。

输入area[3, 3, 0]则返回113.097，N[36 Pi]同样返回113.097，这是一个非常好的开始。

现在我们将k作为自变量，表面积作为因变量，做出一个函数图像。

Plot[area[4, 2, k], {k, -0.2, 0.2}]

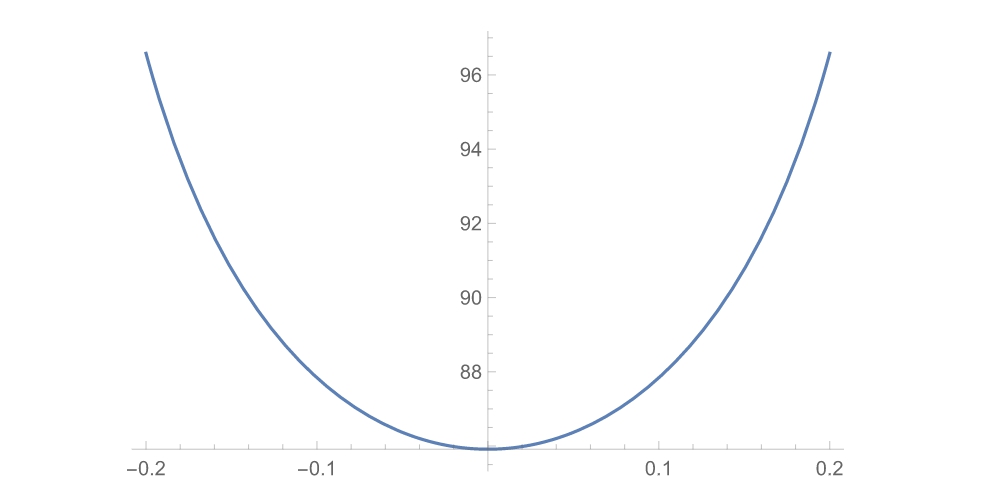
y轴的数值从85.9开始，因此这个图像夸大了k的作用。因此，我们将y轴的值从0开始，用以修正k的影响。

Plot[g[4, 2, k], {k, -0.2, 0.2}, PlotRange -> {0, 100}]

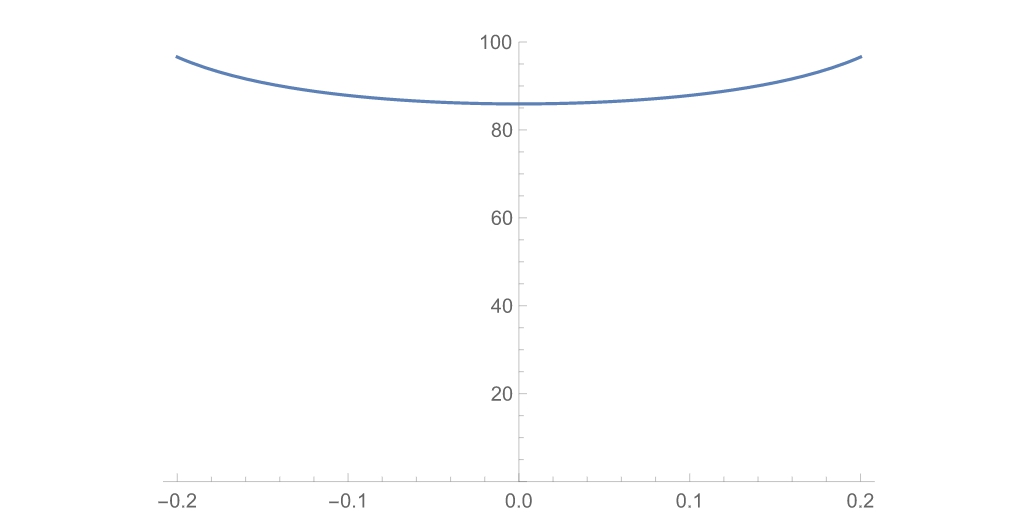
对于体积而言，鸡蛋与椭球之间大约差了一个参数为k的二次函数项。

 

 

关注 哆嗒数学网 每天获得更多数学趣文