曾经最基础的高考题目，却让99%的考生马失前蹄

 

原文作者，李迈新，《挑战极限思维：勾股定理的365种证明》作者。

 

关注 哆嗒数学网 每天获得更多数学趣文

 

每年的高考试卷，最受全社会关注的自然是语文的作文题,一个好的作文题目或者题材，会引起全社会的关注和,有的甚至可以影响好几年，当真是"余音绕梁，三日不绝"。

 

相比之下,数学题目就没那么容易让人记住了,比如在下就是95年参加高考的,那年的题目别说数学，就是语文作文是啥，现在也想不起来了。

不过凡事都没有绝对的，有些数学题目，不仅会让当年的考生终身不忘，还会让后来者胆战心惊，而且老师还会在课堂上敲黑板，画重点，防止重蹈覆辙。

下面要说的这道高考真题,历史已经比较久远(1979年的高考数学试卷第四大题)，但是影响绝对空前，它是当年考生心中永远的痛，让人终身难忘.因为这道题的得分率不到1%，也就是全国99%的考生都被这道题坑了一下。

下面是这道题的真容，1979年普通高等学校招生全国统一考试理科数学试题：

 

叙述并证明勾股定理。

 

是的，你没看错，就是这道题让无数考生竞折腰，原因么，就象萨苏原文(http://blog.sina.com.cn/s/blog_476745f6010003pz.html)说的“对高考的学生来说，这实在太简单了，就是因为太简单了，根本没有几个学生还记得这东西怎么证。勾股定理么，简直象地球是圆的那么自然么。但是。。。证明？这东西还要证明么？！”

 

那么，为啥要出这么一道的简单的送分题(实际上是送命题)呢？

 

潘成彪先生出这道题，当然不是因为希望出的简单，而是他认为中学教育不能只注意题海和数学竞赛，而且应该在基础方面让学生打得更扎实一些，用现在的话来讲,就是不忘初心,放得始终。

 

以后的高考数学题里，影响能与之媲美的，印象里大概只有03年的江苏卷了,那一年据说有个胆大包天的文科生考前居然偷出了理科数学的试卷(你没看错，是文科生,然后偷的是理科生的试卷……)，导致临场采用备用卷，于是那年江苏平均分68(卷面满分150)。

 

现在这道勾股定理的高考题之所以让人难忘，事后看来有这么几个原因：

 

(1)出题人潘成彪先生虽然是著名数学家，但是当时时有保密制度，出题人的姓名是不对外公开的，所以很多考生快30年后还不知道自己的仇人是谁，自然就更加好奇,自然就难忘了。想比之下，江苏的那届学子还是幸运的，至少还知道出题人是葛军，人送外号葛大爷。(不了解这位大神的请自行百度)

(2)如果真是题目出的特别变态，比如超纲或者用到了很难想到的技巧（也就是题目出的比较活），那考生也只能承认自己智商不够，认赌服输，不大会找出题人的麻烦.但是这道题目显然并不难，只需要初中的几何知识，更确切的讲，就是初中几何课本的原题.换了你，在高考时遇到这么一个题目，明知自己学过，但是就是想不起来答案，那肯定是窝火+闹心自然就难忘了。

 

凡事一有开头，就必然有后来的仿效者。这种直接让考生证明教材中重要定理的头一开，第2年（1980年）的数学出题者便照方抓药，就出了一道，1980年理科四题：

写出余弦定理（只写一个公式即可），并加以证明。

 

大概是考虑到老这么搞还是容易被猜题，再者教材里的重要定理就那么些，高考又不允许出重复题目，考一个就少一个，于是80年之后基本上没有这么干的了，直到30年后的四川为了向前人致敬，于是来了一道，四川2010 第9大题：

 

证明两角和的余弦公式 并由此推导出证明两角和的正弦公式。

 

不过在四川之前，2009的考研命题人或许是受到了某种启发，也玩了一次仿古，于是那年的数学1(也包括数学2和数学3)就有了下面的题目，2009年全国硕士研究生入学考试数学一试题：

 

证明拉格朗日中值定理。

最后，给两个勾股定理的经典证法

 

证法一：把两个边长为a和b的正方形进行拼接，然后分割成4个直角三角形加一个小正方形，然后再把他们拼接成一个边长为c的大正方形.立得a²+b²=c² 。

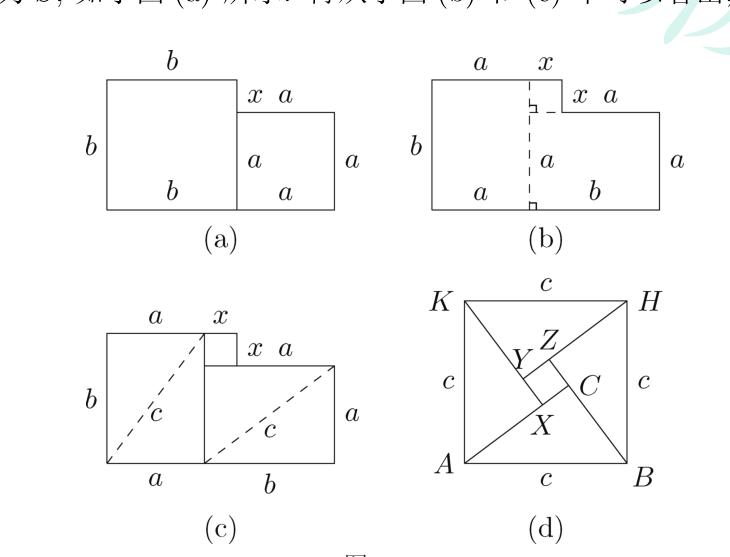
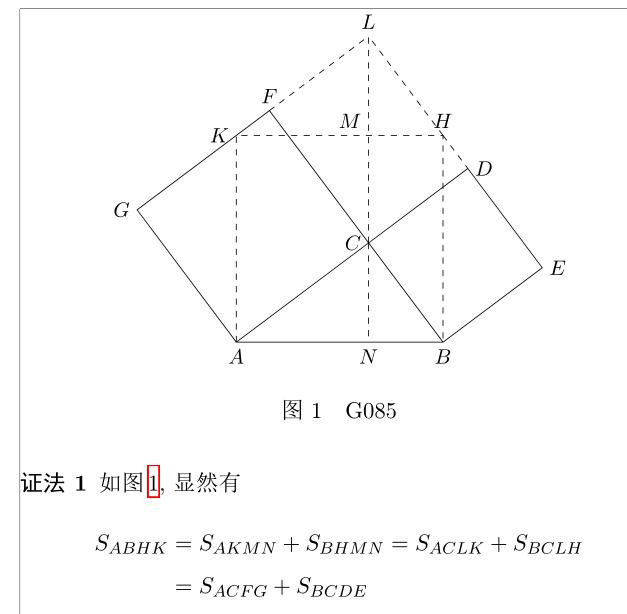
第2个证法，利用等底等高的平行四边形面积相等，可以得到。