鸭蛋上的高数题

 

本文作者系华东师范大学数学系林磊

 

我们华东师范大学数学系在开放接受外校的插班生初期进行的复试时，曾经出过这样一道数学分析题：

设$A$、$B$是一个鸭蛋壳形状的曲面上距离最远的两点。证明：过$A$点的切平面与过$B$点的切平面相互平行.

首先，我们来看看命题人希望看到的解答：

解法一：设该曲面为$\Gamma:G(x,y,z)=0$。$A(x_1',y_1',z_1')$，$B(x_2',y_2',z_2')$，是$\Gamma$上使距离平方：

$$|AB|^2=(x_1'-x_2')^2+(y_1'-y_2')^2+(z_1'-z_2')^2$$

达到最大，且满足限制条件

$$G(x_1',y_1',z_1')=0,~\text{及}~~G(x_2',y_2',z_2')=0$$

的两点. 于是，根据拉格朗日乘数法，考虑函数

$$F(x_1,y_1,z_1,x_2,y_2,z_2)=(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2+\lambda G(x_1,y_1,z_1)+\mu G(x_2,y_2,z_2)$$

则令函数$F$的各变$(x_1',y_1',z_1',x_2',y_2',z_2')$处的偏导数为零，得

$$ 2(x_1'-x_2')+\lambda G_x(x_1',y_1',z_1')=0\\ ~\\ 2(y_1'-y_2')+\lambda G_y(x_1',y_1',z_1')=0\\ ~\\ 2(z_1'-z_2')+\lambda G_z(x_1',y_1',z_1')=0\\ ~\\ 2(x_1'-x_2')+\mu G_x(x_2',y_2',z_2')=0\\ ~\\ 2(y_1'-y_2')+\mu G_y(x_2',y_2',z_2')=0\\ ~\\ 2(z_1'-z_2')+\mu G_z(x_2',y_2',z_2')=0\\ $$

所以，

$$\dfrac{x_1'-x_2'}{G_x(x_1',y_1',z_1')} = \dfrac{y_1'-y_2'}{G_y(x_1',y_1',z_1')}= \dfrac{z_1'-z_2'}{G_z(x_1',y_1',z_1')}~~~~~~~~~~(1) \\~\\ \dfrac{x_1'-x_2'}{G_x(x_2',y_2',z_2')} = \dfrac{y_2'-y_2'}{G_y(x_2',y_2',z_2')}= \dfrac{z_1'-z_2'}{G_z(x_2',y_2',z_2')}~~~~~~~~~~(2) $$

于是，由$(1)$式，非零向量$(x_1'-x_2',y_1'-y_2',z_1'-z_2')$与向量$\vec{n_1}=( G_x(x_1',y_1',z_1'),G_y(x_1',y_1',z_1'),G_z(x_1',y_1',z_1'))$共线，同理，由$(2)$式，非零向量$(x_1'-x_2',y_1'-y_2',z_1'-z_2')$与向量$\vec{n_2}=( G_x(x_2',y_2',z_2'),G_y(x_2',y_2',z_2'),G_z(x_2',y_2',z_2'))$共线，从而，过$A$点的切平面的法向量$\vec{n_1}$与过$B$点的切平面的法向量$\vec{n_2}$共线，所以，两切平面平行。

考试下来，此题几乎没有人得分. 分析下来，学生对题目不理解，无法将描述性的语言转化为数学语言，甚至都没有给出曲面的方程！实际上，所谓鸭蛋壳形状的曲面是指一个光滑的凸的封闭曲面。 而光滑的是指曲面在任意点处都有切平面存在，即可假设定义曲面$\Gamma$的函数$G(x,y,z)$在任意点处都有至少连续的一阶偏导数，且偏导数不全为零。 许多学生根本就没有想到可以自己假设曲面的方程! 当然，更没法想到此题实际上是一道条件极值的问题，并可以应用拉格朗日乘数法。

有一个学生对曲面方程做了这样的假设：

$$\Gamma':~\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1~\text{其中}~a>b>c>0$$

然后断言，$A(-a,0,0)$，$B(a,0,0)$是$\Gamma'$上距离最远的两点。于是过这两点的切平面都与$yOz$平面平行。但是，我们知道，鸭蛋是有大头与小头的，所以它并不是中心对称的，而椭球面太完美了！所以曲面太特殊，不够一般化。另外，就是对于椭球面，$x$轴上的两顶点是椭球面上距离最远的两顶点也不是个显然的事实，所以这个证明基本是不能得分的。

下面，我们利用三角不等式来证明上述事实 (此证明受湖北武汉的陈起航老师的启发，在此表示感谢)：

设$P(x_1,y_1,z_1)$，$Q(x_2,y_2,z_2)$是曲面$\Gamma'$上的任意两点，则 $$|OP|=\sqrt{x_1^2+y_1^2+z_1^2}=a\sqrt{\dfrac{x_1^2}{a^2}+\dfrac{y_1^2}{a^2}+\dfrac{z_1^2}{a^2}}\le a\sqrt{\dfrac{x_1^2}{a^2}+\dfrac{y_1^2}{b^2}+\dfrac{z_1^2}{c^2}}=a$$

同理，$|OQ|\le a$，从而$|PQ|\le|OP|+|OQ|\le 2a$。且从上述不等式取等号的条件分析，等号仅当$P$，$Q$取曲面$\Gamma'$在$x$轴上的两交点时才成立。因此，$\Gamma'$上的两点间的最大距离是$2a$，且$A$、$B$是使距离为$2a$的唯一点。

但事实上，就是不用多元函数的条件极值的方法，我们还是可以完成这个题目的证明的. 请看下面的解法。

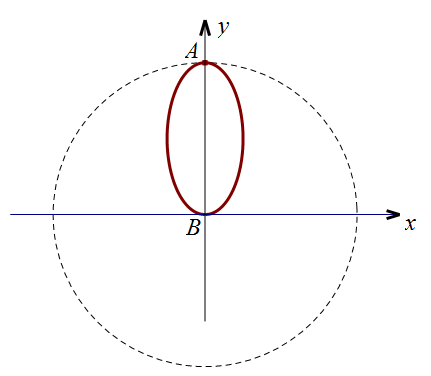
解法二：过$A$点与$B$点任取一平面$\pi_1$，设与曲面$\Gamma$的交线为$\alpha$，这是一条过$A$点与$B$点的封闭的平面曲线. 以$B$为原点，$\overline{BA}$为$y$轴正向，建立平面直角坐标系。由于$A$点与$B$点是曲线$\alpha$上距离最远的两点，于是，曲线$\alpha$在以$B$为圆心，$|AB|$为半径的圆内(或圆上)，从而曲线$\alpha$在$A$点取得极大值，则根据费马引理，曲线$\alpha$在$A$点处的切线$l_1$平行于$x$轴，即$l_1\perp AB$。同理，如果过$A$点与$B$点取另一平面$\pi_2$，得与曲面$\Gamma$的交线为$\beta$，则平面曲线在$A$点的切线$l_2\perp AB$。由于$l_1$与$l_2$ 是以$A$为交点的相交直线，且它们都是曲面$\Gamma$在$A$点的切线，因此这两直线确定了过$A$点的切平面（注意：切平面的存在性是已知的！），$\overline{AB}$就是该切平面的法向量。 同理，$\overline{AB}$也是曲面过$B$点的切平面的法向量，于是，过这两点的切平面平行！

注：解法二将一个空间的多元函数的问题通过考虑曲面与平面的截线，转化成了一个平面的问题，再通过一元函数的结论，得到了证明. 这种解题的方式比较特别，也属于化繁为简，或化难为易的方法。

此外，利用这一方法我们可以看到满足题目结论的曲面不一定非要是鸭蛋的壳，它也完全可以是一个土豆的皮，即我们并不一定要求该曲面是凸的！它完全可以象土豆那样有凹点！因为从我们的证明中看到，当$A$、$B$是曲面上距离最远的两点时，它们一定是凸点，所以，其他地方是不是凸点无所谓。

我们姑且将这种证明方法称为切土豆法！这是家庭主妇都熟悉的方法！

 

 

 

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

​