来来来，做一个黎曼重排定理的实验吧！

 

作者：辻顺平 ，日本趣味数学普及工作者。

翻译，mathyrl，哆嗒数学网翻译组成员。

 

关注 哆嗒数学网 每天获得更多数学趣文

 

 

今天的主题是黎曼重排定理。定理断言，“条件收敛的实数项级数通过重排可以收敛到任意实数”。我们接下来将要对此详细说明，暂时看不懂这个定理的人也请放心。

 

无穷级数绝对收敛是指，级数各项取绝对值也收敛。

 

就像“绝对收敛”这个名称的字面意思那样。

 

相对地，条件收敛是指无穷级数收敛但不是绝对收敛。

 

比如，平方数的倒数之和是绝对收敛。

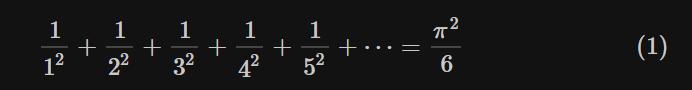
自然数的倒数的交错级数是条件收敛。

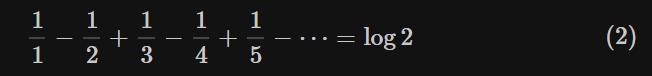
也许会有人提出疑问“为什么要关心绝对收敛和条件收敛呢？”，这是有原因的。

绝对收敛级数，不论哪种求和顺序都收敛到同一个值。总之，不需要关心求和顺序。

另一方面，对于条件收敛级数，收敛的值随着求和顺序而改变。条件收敛也太顽皮了呢。

例如，式（2）的级数收敛到log2，我们改变求和顺序如下：

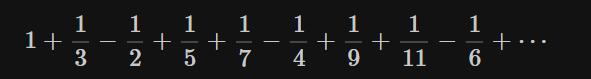
求和收敛到  3log2/2。（计算过程请自行确认即可）

更有趣的是，根据本文开头提到的黎曼重排定理，对于条件收敛级数，通过改变求和顺序，可以使级数收敛到任意实数。

 

不管怎么说，“任意的实数”给人很不显然的感觉呢。

定理的完整内容和证明，参见网上的其他。

总之定理是可以证明的。在这里没有详细证明，会让人迷迷糊糊摸不着头脑，感觉好像很难的样子。

想要好好的理解定理，试着去看前面提到的证明，是可以比预想中更清晰地理解的。而且，如果仔细地阅读证明，就会注意到证明之中包含了让级数收敛到任意实数的方法。

不管怎么说，我们能让级数收敛到喜欢的实数值，这应该是很有趣的！

前面的引子说了这么长，今天的文章要介绍的是让条件收敛级数收敛到期望实数的步骤。

让级数收敛到期望实数的步骤
（需要准备的东西）

1、 条件收敛级数（1个）：

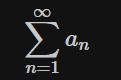
这里的a_n全部为实数
2、 想要收敛到的实数（你喜欢的数都可以）：r

（步骤）

①将原级数数列分为“正项组成的数列”和“负项组成的数列”。
※由于假定原级数为条件收敛，因此我们知道划分出来的两个级数都发散。

②只使用“正项组成的数列”的项求和，使得部分和恰好大于要收敛到的实数。
※因为正项组成的级数是发散级数，对于任意实数，存在有限部分和大于这个实数。

③只使用“负项组成的数列”的项求和，使得部分和恰好小于要收敛到的实数。

④使用“正项组成的数列”余下的项求和，使得部分和再一次恰好大于要收敛到的实数。

⑤使用“负项组成的数列”余下的项求和，使得部分和再一次恰好小于要收敛到的实数。

⑥接下来重复步骤④和⑤

仅此而已。

通过以上步骤，级数确实收敛到指定的实数。（详细证明请参照相关资料）

让交错级数收敛到期望的实数

接下来我们试着具体实行上面的步骤。

实验对象当然是交错级数了：

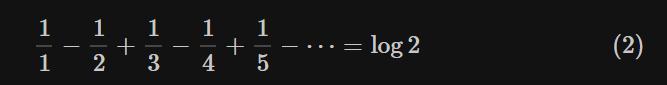
作为具体的例子，我们试着改变求和顺序使级数收敛到r=2。

①把级数数列划分为“正项组成的数列”

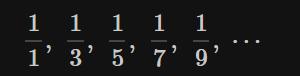
和“负项组成的数列”

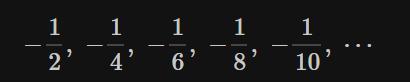
②使用“正项组成的数列”的项求和，使得部分和恰好大于r=2。实际上计算到1/15，部分和大于2：

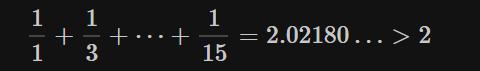
③使用“负项组成的数列”的项求和，使得部分和恰好小于2。实际上只加上-1/2，部分和就小于2：

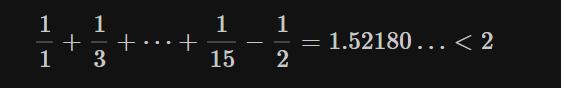
④使用“正项组成的数列”余下的项求和，使得部分和再次恰好大于2：

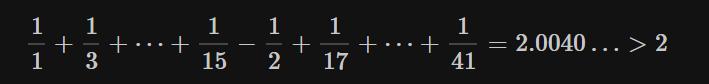
⑤使用“负项组成的数列”余下的项求和，使得部分和再次恰好小于r=2：

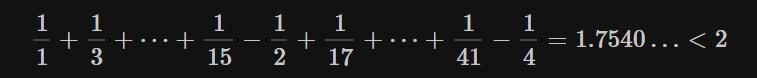
⑥接下来重复④和⑤，于是就得到收敛于r=2的级数：

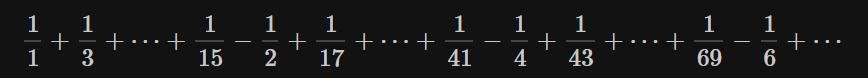
有趣吧！

收敛的情形用图像表示如下：

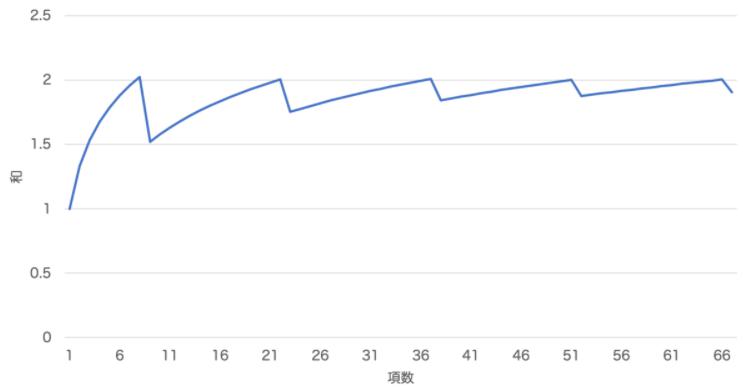
（改变求和顺序的交错级数收敛到2。）

同样，改变求和顺序而收敛到圆周率π的交错级数如下所示：

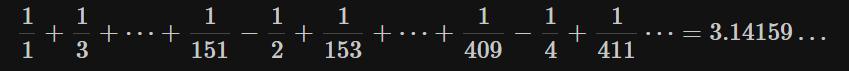
（改变求和顺序的交错级数收敛到3.14159…）

看起来的确是收敛到3.14159…呢！

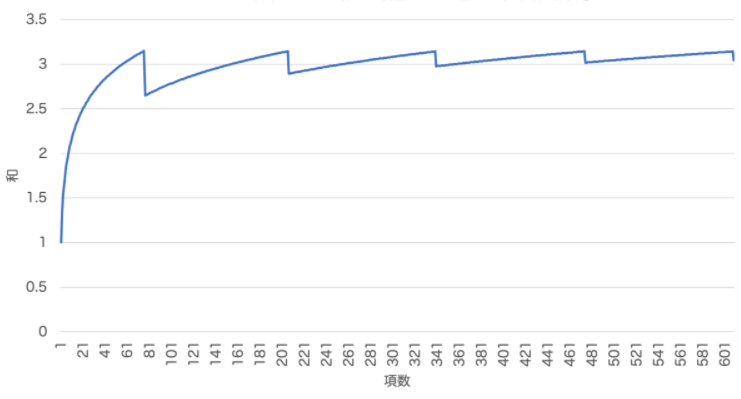
理论上，不管是1.41421356…也好，5000万亿也好，级数能收敛到你喜欢的实数值。

用于验证的python代码如下所示。有兴趣的话请试着把玩一下。

r = 3.14159265 # 在这里输入收敛到的实数值
#r = 2 # 在这里输入收敛到的实数值

def a_pos(n_pos):
    return 1/(2*n_pos+1)

def a_neg(n_neg):
    return -1/(2*n_neg+2)

n_pos = 0
n_neg = 0
sum = 0

pos_neg_flag = 1   # 1: pos, -1: neg

for i in range(5):
    print("(ans) ".format(2*n_pos+1), end='')
    if pos_neg_flag > 0:
        while sum < r:
            sum += a_pos(n_pos)
            #print(sum)
            print("+ 1/{}".format(2*n_pos+1), end='')
            n_pos += 1
    else:
        while sum > r:
            sum += a_neg(n_neg)
            #print(sum)
            print("- 1/{}".format(2*n_neg+2), end='')
            n_neg += 1
    print(" =",sum)
pos_neg_flag *= -1   # pos, neg改变符号 

运行代码后是这样子的：
(ans) + 1/1+ 1/3+ 1/5+ 1/7+ 1/9+ 1/11+ 1/13+ 1/15+ 1/17+ 1/19+ 1/21+ 1/23+ 1/25+ 1/27+ 1/29+ 1/31+ 1/33+ 1/35+ 1/37+ 1/39+ 1/41+ 1/43+ 1/45+ 1/47+ 1/49+ 1/51+ 1/53+ 1/55+ 1/57+ 1/59+ 1/61+ 1/63+ 1/65+ 1/67+ 1/69+ 1/71+ 1/73+ 1/75+ 1/77+ 1/79+ 1/81+ 1/83+ 1/85+ 1/87+ 1/89+ 1/91+ 1/93+ 1/95+ 1/97+ 1/99+ 1/101+ 1/103+ 1/105+ 1/107+ 1/109+ 1/111+ 1/113+ 1/115+ 1/117+ 1/119+ 1/121+ 1/123+ 1/125+ 1/127+ 1/129+ 1/131+ 1/133+ 1/135+ 1/137+ 1/139+ 1/141+ 1/143+ 1/145+ 1/147+ 1/149+ 1/151 = 3.147125289923645

(ans) - 1/2 = 2.647125289923645

(ans) + 1/153+ 1/155+ 1/157+ 1/159+ 1/161+ 1/163+ 1/165+ 1/167+ 1/169+ 1/171+ 1/173+ 1/175+ 1/177+ 1/179+ 1/181+ 1/183+ 1/185+ 1/187+ 1/189+ 1/191+ 1/193+ 1/195+ 1/197+ 1/199+ 1/201+ 1/203+ 1/205+ 1/207+ 1/209+ 1/211+ 1/213+ 1/215+ 1/217+ 1/219+ 1/221+ 1/223+ 1/225+ 1/227+ 1/229+ 1/231+ 1/233+ 1/235+ 1/237+ 1/239+ 1/241+ 1/243+ 1/245+ 1/247+ 1/249+ 1/251+ 1/253+ 1/255+ 1/257+ 1/259+ 1/261+ 1/263+ 1/265+ 1/267+ 1/269+ 1/271+ 1/273+ 1/275+ 1/277+ 1/279+ 1/281+ 1/283+ 1/285+ 1/287+ 1/289+ 1/291+ 1/293+ 1/295+ 1/297+ 1/299+ 1/301+ 1/303+ 1/305+ 1/307+ 1/309+ 1/311+ 1/313+ 1/315+ 1/317+ 1/319+ 1/321+ 1/323+ 1/325+ 1/327+ 1/329+ 1/331+ 1/333+ 1/335+ 1/337+ 1/339+ 1/341+ 1/343+ 1/345+ 1/347+ 1/349+ 1/351+ 1/353+ 1/355+ 1/357+ 1/359+ 1/361+ 1/363+ 1/365+ 1/367+ 1/369+ 1/371+ 1/373+ 1/375+ 1/377+ 1/379+ 1/381+ 1/383+ 1/385+ 1/387+ 1/389+ 1/391+ 1/393+ 1/395+ 1/397+ 1/399+ 1/401+ 1/403+ 1/405+ 1/407+ 1/409 = 3.143260498314515

(ans) - 1/4 = 2.893260498314515

(ans) + 1/411+ 1/413+ 1/415+ 1/417+ 1/419+ 1/421+ 1/423+ 1/425+ 1/427+ 1/429+ 1/431+ 1/433+ 1/435+ 1/437+ 1/439+ 1/441+ 1/443+ 1/445+ 1/447+ 1/449+ 1/451+ 1/453+ 1/455+ 1/457+ 1/459+ 1/461+ 1/463+ 1/465+ 1/467+ 1/469+ 1/471+ 1/473+ 1/475+ 1/477+ 1/479+ 1/481+ 1/483+ 1/485+ 1/487+ 1/489+ 1/491+ 1/493+ 1/495+ 1/497+ 1/499+ 1/501+ 1/503+ 1/505+ 1/507+ 1/509+ 1/511+ 1/513+ 1/515+ 1/517+ 1/519+ 1/521+ 1/523+ 1/525+ 1/527+ 1/529+ 1/531+ 1/533+ 1/535+ 1/537+ 1/539+ 1/541+ 1/543+ 1/545+ 1/547+ 1/549+ 1/551+ 1/553+ 1/555+ 1/557+ 1/559+ 1/561+ 1/563+ 1/565+ 1/567+ 1/569+ 1/571+ 1/573+ 1/575+ 1/577+ 1/579+ 1/581+ 1/583+ 1/585+ 1/587+ 1/589+ 1/591+ 1/593+ 1/595+ 1/597+ 1/599+ 1/601+ 1/603+ 1/605+ 1/607+ 1/609+ 1/611+ 1/613+ 1/615+ 1/617+ 1/619+ 1/621+ 1/623+ 1/625+ 1/627+ 1/629+ 1/631+ 1/633+ 1/635+ 1/637+ 1/639+ 1/641+ 1/643+ 1/645+ 1/647+ 1/649+ 1/651+ 1/653+ 1/655+ 1/657+ 1/659+ 1/661+ 1/663+ 1/665+ 1/667+ 1/669+ 1/671+ 1/673 = 3.141796661628686

尽管证明看起来很抽象，如果具体地实行其中的步骤，证明就变得容易理解了。这次的情形就是这样一个真正的实例。

今天就先到这里吧。

 

 

关注 哆嗒数学网 每天获得更多数学趣文