有趣的搬空银行游戏：一个巧妙的展示不变量思想的好案例

 

本文编译自Alex Bellos于2019年10月7日发表于英国《卫报》网站的文章

编译：Math001

 

 

关注 哆嗒数学网 每天获得更多数学趣文

 

今天，我们来玩一个游戏。玩这个游戏需要一个无限行无限列的表格，以及三枚硬币。三枚硬币放在表格的左上角。就像下面图中表示的那样。

游戏只有一种操作。你可以拿掉任何一枚硬币，但是需要马上在这枚硬币的右边和下边的格子里补上两枚硬币。比如，如果你拿掉了上方第二个硬币，你需要按下图中的方式，马上补上两枚。

再补充一个规则吧。只有一枚硬币右边和下边的格子全都是空格子的时候，你可以拿掉硬币，并补上两枚。哪怕有一个格子不是空的，这枚硬币都不能拿掉。你就只能拿别的按规则可以拿掉的硬币。

 

我们把左上方2×2的格子圈出来，把它叫做银行，如下图红框部分。

你会直观地感受到，整个游戏过程中，硬币逐渐增多，总体是向右下方流动的。

 

我们的问题是，你有什么策略，可以让银行中的硬币全部流出银行。就是说左上2×2的格子中，不再有任何一枚硬币。或者，你会觉得总会有硬币留在银行中，但你需要清晰精准地说明这一点。

 

这个问题其实有点难的， 你可以做做实验，多想一会儿。待会儿我们解谜的时候，你会感受到数学的神奇。(在一串长空格后，我们开始解密)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

解密开始：

 

在具体说明这个问题之前，你可能做了很多次实验了。是不是开始怀疑，如果严格按照游戏规则，是不可能把银行清空的。

 

对的！如果你有这个想法，那恭喜你，这就是这个问题的正确答案。那么，剩下的事情就是严谨地证明你的猜想。

 

证明的方法也许不唯一，这里讲述一个本人认为非常巧妙的一个办法。

 

我们的证明过程会去设计一个不变量，利用这个不变量来说明按照游戏规则，我们无法搬空银行。不变量是一个数学概念，简单的说，它表达的是无论局面如何变化，那些在万变之中永远不变的东西。不变量的思想几乎贯穿数学这门学科的所有分支，甚至有观点认为，数学本身就是研究各种不变量的学科。

 

为了说明问题，我们做一些准备工作。我们用如下的方式给每个格子标记一个数。

 

 

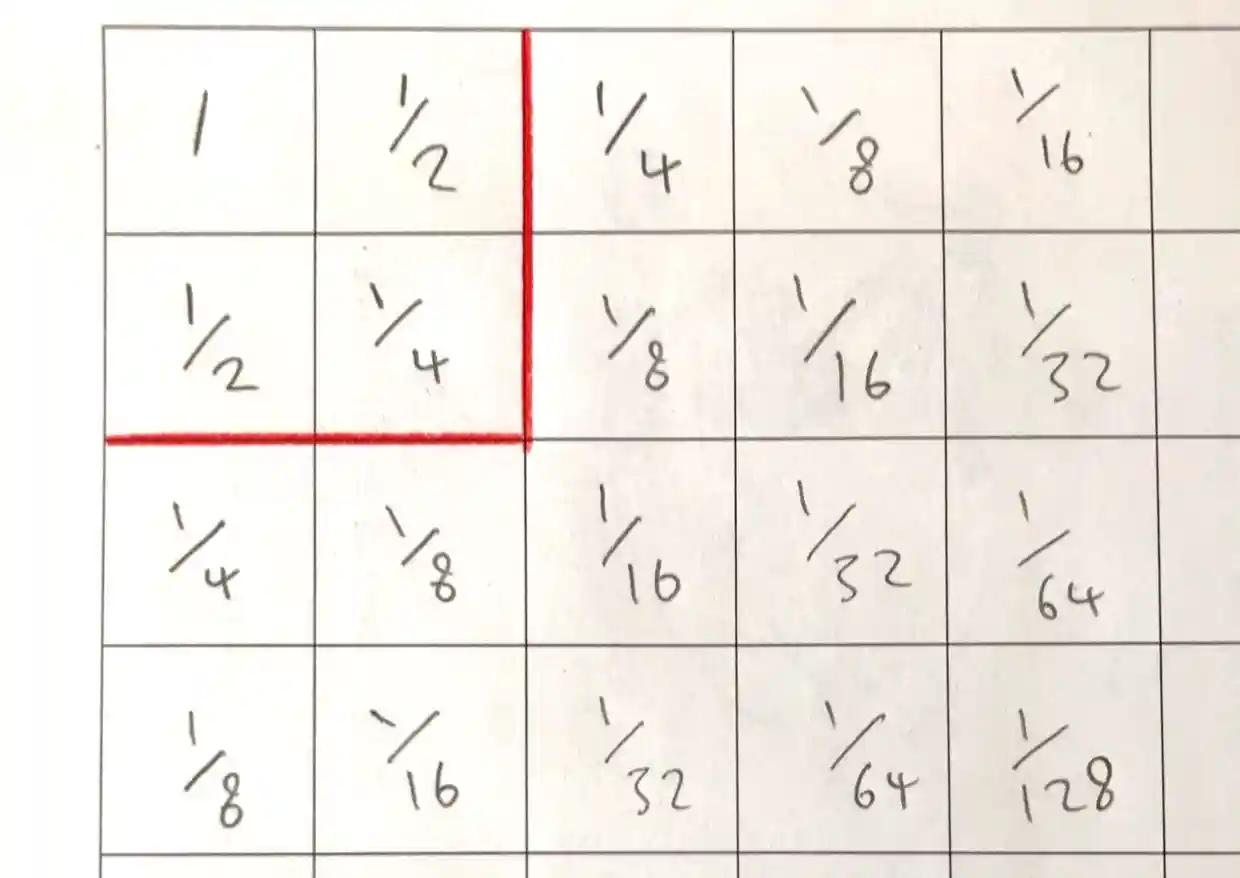
标记的规则是这样的：

 

第一排，从左边第一个开始分别标记1,1/2,1/4,...，总之右边的那个数是之前数的一半。

 

第二排，从左边第一个开始分别标记1/2,1/4,1/8,...，就是起始的数是上一排的一半，但总是保证右边的那个数是之前数的一半。

 

第三排，继续1/4,1/8,1/16,...

 

以此类推……

 

表格标记完后，你会发现，你任意取一个格子和它右边以及下边相邻格子标记的数都是这个格子的一半。

 

准备工作完毕，我们来设计我们的不变量了。

 

首先，我们来看看，所有格子的数加起来会等于多少。这里有无穷个数求和，我们的策略是先求出每一行的和，再把这些和加起来。

 

第一行就是，1 + 1/2 + 1/4 + ... ，结果是2 ；

 

第二行，1/2 + 1/4 + 1/8 + ... ， 结果是 1 ；

 

第三行，1/4 + 1/8 + 1/16... ， 结果是 1/2 ；

 

……

 

最后再来 2 + 1 + 1/2 + ... ， 加起来等于4 。

 

就是说所有数字加起来的和是4。

 

我们再来看看规则。每次操作，我们都会把原本的硬币去掉，并在右侧和下侧添加上两枚新的硬币。虽然，表格中的硬币会增加一个，但是替换上的硬币覆盖格子中标记数的总和之前那枚硬币覆盖标记数是相等的。这意味着，无论多少此操作，所有硬币覆盖格子中标记数的总和不变。

 

那么，按照初始的三个硬币摆放的位置。三枚硬币覆盖的标记数之和是1 + 1/2 + 1/2 = 2。银行中，标记数之和是2 + 1/4 = 9 . 要把所有硬币在银行内清空，意味着银行内没有硬币，所有硬币都在银行外。根据之前的分析，就是说要达到一种状态，银行外硬币覆盖的标记数之和保持初始的2不变。但是，银行外标记数之和为 4 - 9/4 = 7/4 ，比2小。

 

所以不能清空银行。 

 

另外，实际上通过之前的讨论，你可以证明：哪怕把硬币完全清理出初始的三个位置，都是不可能的。因为，剩余的标记数之和是2，需要无限个硬币才能达到。而有限次操作，最多生成有限枚货币。

 

 

关注 哆嗒数学网 每天获得更多数学趣文