26岁博士破解埃尔德什本原集猜想

 

关注 哆嗒数学网 每天获得更多数学趣文

 

 

根据牛津大小数学研究所官网消息。牛津大学数学博士李奇曼(Jared Duker Lichtman)证明了埃尔德什众多数论猜想的其中一个——埃尔德什本原集猜想。

专业数学的成果往往很难被普通大众理解，而这个猜想却不一样，问题本身是中学生能明白问题说什么的。借着这个机会，我们来介绍一下。

首先，一个正整数集合A如果里面任意两个元素都都没有一个是另外一个的倍数的情况发生，那么我们说这个这个集合叫做本原集。

比如如果A是所有质数组成的集合，那么A是本原集。

如果A是正好是有2两个质因数的那些正整数组成的结合，那么A是本原集。

对于任意正整数k，如果A是正好有k个质因数的那些正整数组成的集合，那么A是本原集。

对于一个正整数，如果它所有非本身的因数之和等于其本身，这个数叫做完美数(比如6非本身的因数有1,2,3，这三个数加起来正好是6，所以6是一个完美数。另外28也是完美数)。如果A是所有完美数组成的集合，那么A是本原集。(证明留作习题，难度是初中级别的)

如果A是本原集，我把A中的每一个数n都取出来，计算一下对应的 n·ln(n)的倒数，再把所有的这些倒数加起来，这样会得到一个计算结果（详细的符号见下图），我们把这个数记作f(A) 。

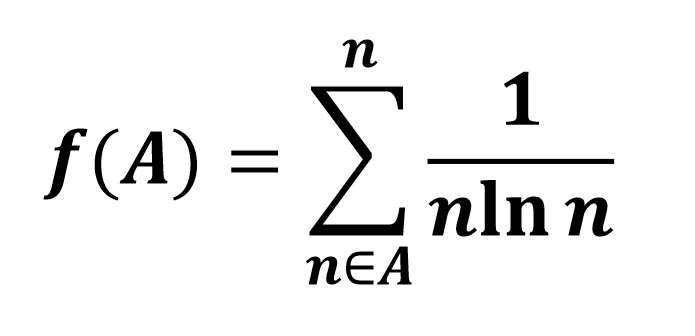
1935年，埃尔德什本人证明了f(A)有一个统一的常数上界。

1988年埃尔德什猜想，当A取所有质数的时候，能得到最小的上界。就是说，下面的不等式成立。

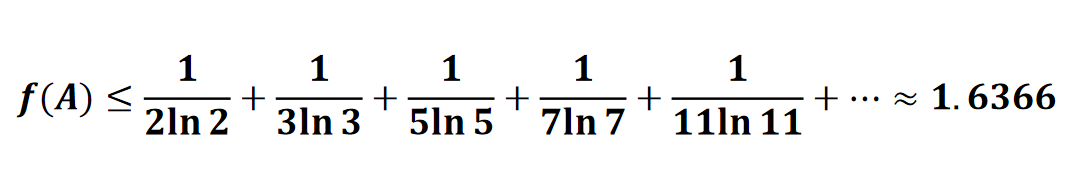
李奇曼今年26岁，他35岁的导师梅纳德(Maynard)也是数论界大名鼎鼎的人物。他导师看到这个证明后先是惊了一下，然后小小的酸了一下：“这运气也太好了吧”。当然梅纳德的同等或超过这个成果的重量级成果很多……

 

关注 哆嗒数学网 每天获得更多数学趣文