张益唐讲座速记：部分解决朗道-西格尔零点问题

张益唐11月8日《关于朗道-西格尔零点猜想》学术报告速记。

 

要点：

1、张益唐没有完全解决朗道-西格尔零点猜想本身，而是解决了一个更弱的一个命题。但这个更弱的问题也是一个突破。原本的表述“本质上”解决朗道-西格尔零点猜想就是在这个部分解决的意义下说的。

2、论文中给的指数2024都还可以改进，按张教授设想改进到几百应该没问题，但是离1的目标这个办法应该不太可能。

3、如果这个方法成立，按张益唐推测，这也许是解析数论的突破。之前都是想办法取构造zn（后文会讲是什么zn)，而这个办法是另外一种操作。

4、论文还没有完全定稿，有很多细节需要补充。尤其是一些计算细节。

 

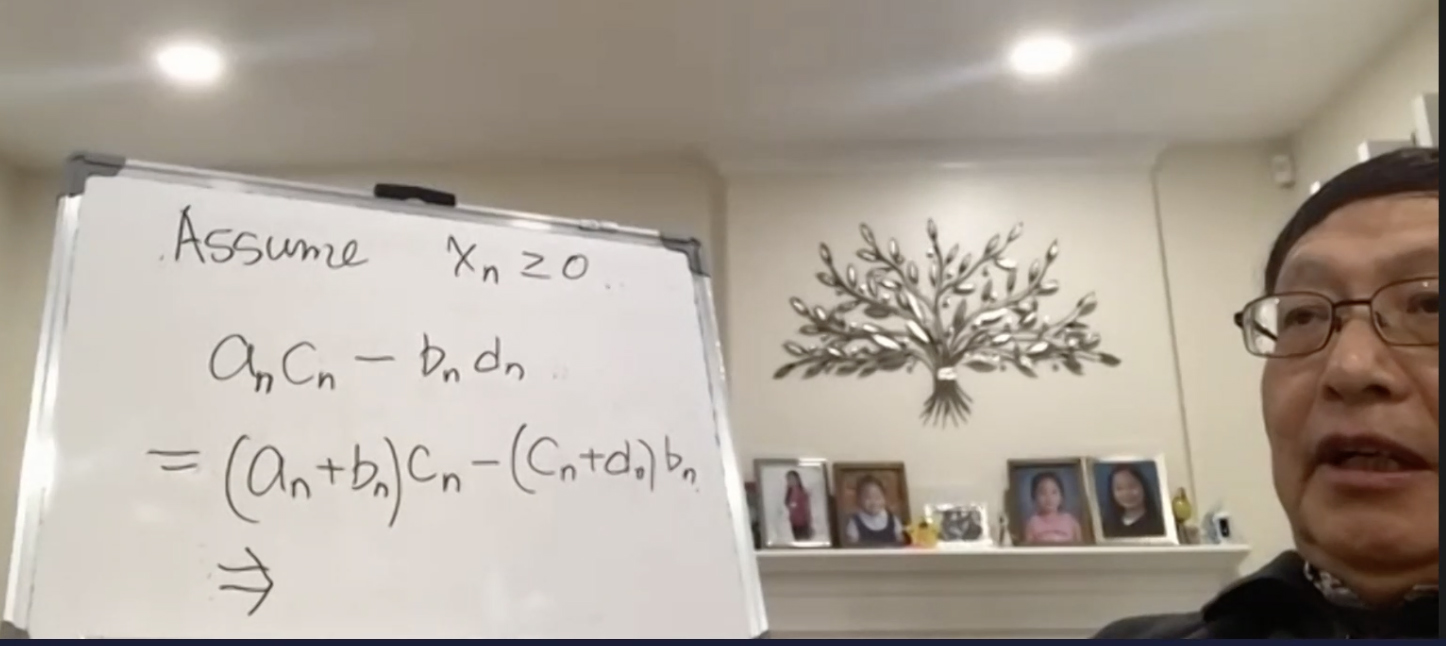
一、问题介绍

 

对于迪利克雷L函数，

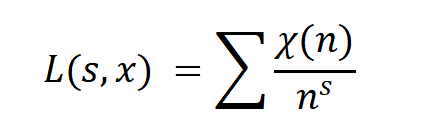
其中χ(n)是实本原狄里克雷特征函数，χ是希腊字母,读作kai。

 

那么，朗道-西格尔零点猜想可以表述为，

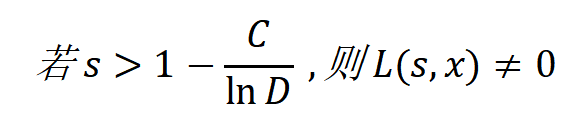
而张益唐教授这篇论文证明的是

 

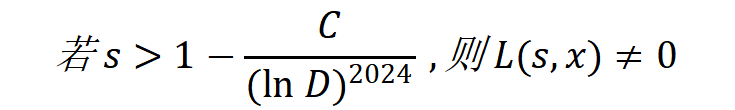
这里，张教授补充。这其实是比黎曼猜想弱得多的猜想，但有媒体说论文有可能推翻黎曼猜想。对于这点，张教授回应是——我没那个本事，也不会有人信。

 

另外，证明过程还会用到一个很初等的恒等式：

 

 

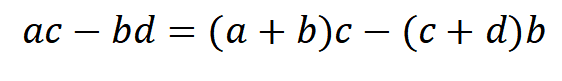
问题拆解

 

对于一个有限长度的实数数列，

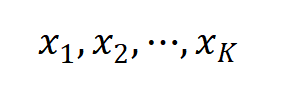
如何判断它们都是大于等于零的，或者说如何知道这里面有没有负数。这样的问题和我们数论问题有什么关系呢？

 

例1：

 

考虑质数的特征函数：

 

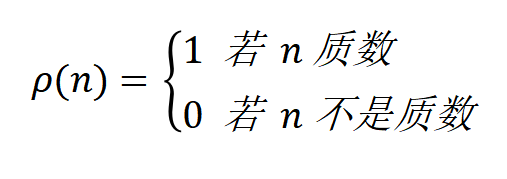
然后对于正整数N，定义长度为N-2的序列xn如下：

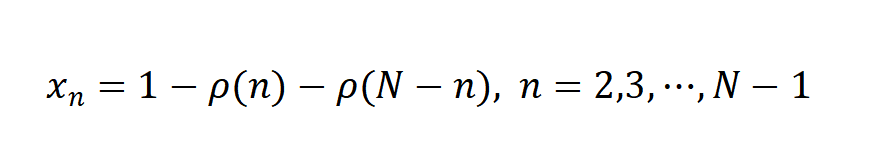
这个序列中要有小于零的数，只能是后两项都等于1 。就是说，xn为负的充要条件是N=n+(N-n)是两个质数的和。

 

那么N取遍所有偶数，如果能证明对所有偶数生成的这些序列中都有负数的话，那就证明了哥德巴赫猜想。

 

 

例2

 

设f(t)是[0,T]上的连续实函数。且有N个零点，t1,t2,...,tN 。这N个零点之间的间隔都大于c，即 t(n+1) > tn + c 。如果0<a<b<c, 且 

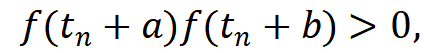
那么就能找到要么同正要么同负的两个数，但是这个办法不总是好用。

 

那么，还可以找一个非负数列yn, 按如下操作判定是否有负数：

而塞尔伯格给了一个改进，我们直接找zn是某个数列yn的平方形式，就是说他改进的流程变成这样：

按张教授介绍，之前做弱孪生质数的办法就是这种。之前他们的估计始终有个ε跨不过去，我就用一种办法把它跨过去了，但用的zn基本上是之前他们做的zn。而后来梅纳德的办法是找了新的zn，就大大改进了结果。

 

回到西格尔零点

问题的办法还是要找个xn小于零，办法还是试图找到zn，然后让和式小于零。但非常难找到，我找到很多能接近零的，但始终跨不过0这个点。

 

新思路

 

张教授的新思路是用不同路径找到两组序列an+bn 和 cn+dn ，满足xn(an+bn)^2 和 xn(cn+dn)^2都和零非常接近。然后利用一通操作（比如柯西不等式）得到矛盾。

假设xn都是大于零的，那么利用之前的那个初等的等式得到：

 

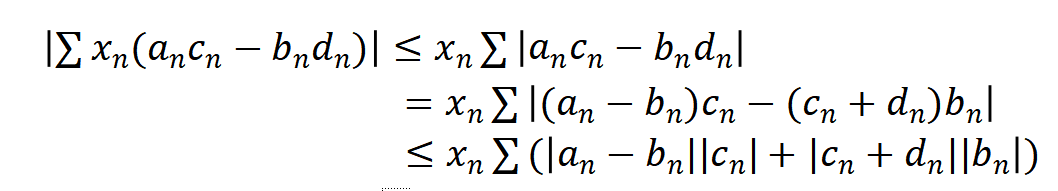
这会导致矛盾。

 

自塞尔伯格以来，人们一直在考虑有没有不是平方形式的yn来做这些问题。但是一直没产生更好的办法。感觉zn平方的办法人们已经做到极致了，应该尝试新的办法。大家肯定想过，不过现在还是在zn平方里在做。如果这个办法奏效，张教授认为应该是一个突破，这个思路可以被用于解决数论中的其他问题。

 

后记

 

提问：你之前说的本质上解决是什么意思？

张教授：（如前文所诉）在这个部分解决的意义下把这个问题的进展做了推进。

 

提问：2024还能改进吗？

张教授：肯定可以，但自己没去算过，感觉上改进到几百应该问题不大。

 

提问：这个成果有还有什么应用？

张教授：在质数等差级数分布上能有很多很好的结果。另外，了解到解析数论和代数数论中的问题也和这个有关，但自己没做这方面研究，不了解具体细节。