从布朗运动、随机微积分到股票买卖
关注微信:DuoDaaMath 每天获得更多数学趣文
作者,小米,哆嗒数学网群友。
1827年,英国植物学家布朗观察了水中悬浮花粉的运动轨迹,他发现,尽管每一时刻花粉的运动杂乱无章,但是却遵循如下的统计规律:在时间T内,花粉运动的平均位移正比于sqrt(T)( sqrt(T)表示T的算术平方根,下同——哆嗒数学网注)。这就是布朗运动的来历。爱因斯坦在1905年发表的关于布朗运动的论文中,利用分子动力学分析布朗运动,提出花粉的运动是水分子无规律撞击的结果。这是第一次对布朗运动的数学解释。但布朗运动的故事并未就此结束。1923年,美国数学家维纳第一次给出布朗运动作为随机过程的数学构造,从此布朗运动成为了概率论中严格化的数学对象。因此,布朗运动在概率论中也称为“维纳过程”。
那究竟什么是布朗运动呢?我们还是想像着花粉的运动。首先,既然花粉的运动是水分子撞击的结果,那么任一时刻之前和之后,花粉的运动应该遵循相同的规律,而且彼此是独立的。其次,花粉运动的规律应该具有尺度不变性。花粉在时间T内平均位移正比于sqrt(T),无论T是1秒钟、1分钟还是1小时,都是一样的,而且sqrt(T)前面的常数也应该与T无关。更进一步,当我们通过正确的时间空间尺度去看观察布朗运动时,观察到的物理规律应该完全一样。例如在10倍的放大镜下,视野中花粉移动1厘米用了1秒钟;那当我们去掉放大镜后(相当于把长度缩小了10倍),同样观察到1厘米的移动就需要100秒钟(相当于钟拨慢了100倍)。这个100:10符合T:sqrt(T)的关系,因而是正确的尺度变换。另一个例子是我们把(1维)的布朗运动轨道画在坐标系中,横轴是时间,纵轴是空间。假设我们把时间轴放大4倍,而把空间轴放大2倍时,看到的轨道应该是一样的(符合相同的规律)。聪明的读者可能看出来了,和雪花、海岸线一样,布朗运动的轨道也是分形。
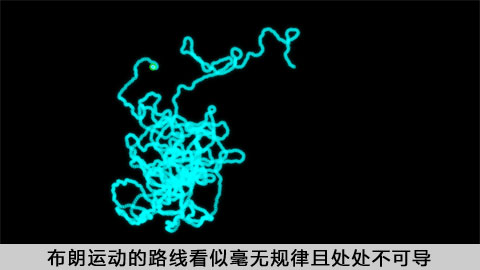
接下来我们要谈谈随机微积分了。随机微积分的最重要的对象就是布朗运动。记得在高等数学的第二型曲线积分中,我们会遇到形如F(t)ds(t)的积分微元,这里s(t)可以是空间中一个粒子运动的轨迹,F(t)是t时刻施加在粒子上的力,那么整个积分就是某段时间内粒子被做的功。高等数学里面我们学习了如何把微元F(t)ds(t)写成F(t)*s'(t)dt的形式,从而问题转化成为了第一型曲线积分。如果我们的粒子像花粉一样做布朗运动,那么微元就应该写作F(t)dB(t)(注:B(t)表示布朗运动--B是布朗的首字母)。我们能不能定义布朗运动的微分B'(t)呢?最短的答案是:不能。因为我们知道,布朗运动在时间T内的位移是sqrt(T),在微元的情况下就是dt的时间微元里面运动了sqrt(dt)。但是微分(我们这里是速度)的定义是空间微元除以时间微元,我们得到了1/sqrt(dt),这是一个无穷大量!所以高等数学中通过微分来转化问题的方法在这里失败了。
有没有其它方法呢?布朗运动的导数虽然没有意义,但是并不代表积分也没有意义。历史上随机积分都好几种不同的定义方式,我们接下来要介绍概率论中应用最广的一种,也就是日本数学家伊藤清首先发展起来的伊藤积分。对时刻[a,b]内的布朗运动,我们可以把[a,b]分成很多个小区间a=t(0)<t(1)<...<t(n)=b,在每一个小区间[t(k),t(k+1)]上认为布朗运动是直线,受力F也是恒力F(t(k))。如果是普通的积分,这一步就是定积分的黎曼和逼近。因为布朗运动不可导,所以对每一条轨道而言,当我们把小区间越分越细时,黎曼和并不存在一个极限。但是,我们并没有充分利用布朗运动的随机性。对于小区间的每一个分划,因为轨道是随机的,所以黎曼和也是一个随机数,用概率论的语言来说就是随机变量。每一条轨道上,随机变量因为轨道的不可微性而不存在极限,在概率论的框架下,这只能说明不存在“几乎处处”的极限。但这只是概率论中最强的一种极限形式。对于随机变量而言,除了几乎处处收敛,还有依概率收敛、Lp收敛、依分布收敛等等,这些概念相信接触过初等概率论中大数定律、中心极限定理的读者都不会陌生。在更弱的收敛意义下,那些黎曼和确实存在极限(当然极限也是一个随机变量,因为布朗运动本来就是随机的)。既然积分能够被定义,而积分和微分又是相反的运算,所以微分在某种意义下也可以说是存在的,这也就是为什么在文献中布朗运动也是可以被“求导”的,而“随机微积分”也就名副其实了。
值得注意的是,伊藤积分和普通微分满足不同的运算规则。像我们熟知的莱布尼茨法则、牛顿-莱布尼茨公式都需要做额外的修改才能在伊藤积分中成立,这些规则可以泛称为“伊藤公式”。伊藤积分还满足概率论中的鞅性质,而鞅又是概率论中一个很好的研究对象。另一方面,注意到我们定义黎曼和时取左端点F(t(k))而非任意点吗?这可是很有讲究的。取左端点、右端点抑或是中点对应3种不同的随机积分,它们满足的运算法则也不相同,其中也只有伊藤积分满足鞅性质。例如,取中点对应的Stratonovich积分是通过光滑化布朗运动再作逼近得到的,它不满足鞅性质,却与普通微积分满足相同的牛顿-莱布尼茨公式,因此深受物理学家们的喜爱。
看到最后,有的读者可能要问,为什么要费那么大力气去定义关于布朗运动的随机积分呢?其实随机微积分的运用十分广泛。例如股票市场中一支股票的升降可以看作某种布朗运动,而持股人的决策--什么时候卖出或买入多少--就和前面例子中的力F充当着相当的作用。随机积分的结果恰好就是一段时间能持股人在给定决策下的收益!知道了这一点,对金融数学中频繁用到随机积分也就不会奇怪了。
关注微信:DuoDaaMath 每天获得更多数学趣文

评论已关闭