万圣节前夜:讲述魔鬼数字与黄金分割比
关注微信:DuoDaaMath 每天获得更多数学趣文
每年的10月31日是万圣节前夜,这是西方一些国家的传统节日。这个节日充满了魔鬼、怪物、死亡、魔法相关的元素,也充满了各种糖果、点心。小孩子们会装扮成各种妖魔鬼怪沿街讨要糖果,经常听到的“不给糖就捣蛋”说的就是这个节日中的场景。所以万圣节前夜的节日气氛是既古灵精怪,又其乐融融的。
这个节日是把邪恶事物转变为美好事物的一天。我们哆嗒数学网的小编今天也应景奉上一篇小文章,说的是把邪恶的魔鬼数字变为美好数字。本文主要思想来自福布斯网站一篇文章。(http://www.forbes.com/sites/kevinknudson/2015/10/29/devilish-trigonometry-linking-the-number-of-the-beast-and-the-golden-ratio/)。
《圣经·启示录》里的故事告诉我们,666这个数字是个邪恶的数字,因为它是魔鬼撒旦的印记(也叫兽的印记)。所以在现实中,很多人会选择这个号码的包间作为万圣节前夜的派对包间。
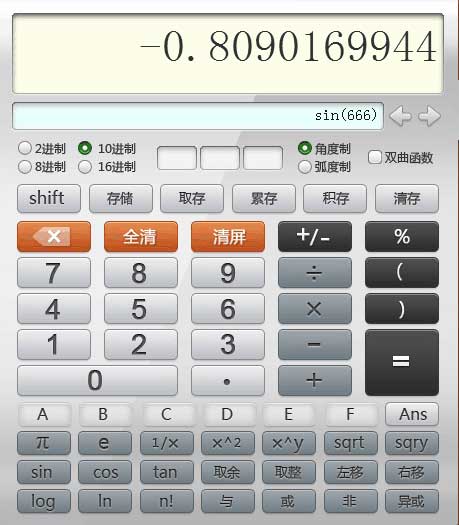
现在,我们要开始施放一个数学“魔法”,将这个魔鬼印记转变了。请打开百度,输入“计算器”,利用百度的计算器计算sin(666°)(按键的时候需要确保666是角度,而不是弧度),你会得到一个结果-0.8090169944……。也许你会问,这个数字有什么可爱之处?别急,在揭开障眼法之前,我们先一起回忆下另外一个数字——黄金分割比φ。
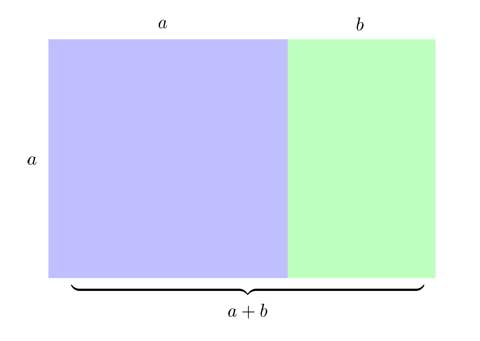
如图,我们把边长为a的正方形(蓝色部分)的一条边延长b,延长后得到的大长方形满足a/b=(a+b)/a。那么a/b就被定义为黄金分割比φ。如果我们令b=1,就能很快得到φ的值,它其实是二次方程a²=a+1的正根:
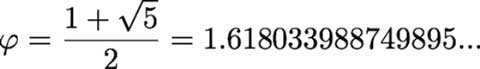
然后呢?恩,如果我们把φ除以2,得到0.8090169944……, duang!duang!duang!看到了吗?它看上去正好是sin(666°)的相反数。
虽然计算器的魔法已经施完,但是我们还是要用一个严谨的数学证明来真正揭开这个障眼法。
当然,如果你对一些数学结论比较熟悉,其实已经是很容易看出的结果了。不过我们还是要再解释一下。利用正弦函数的周期性和奇偶性,我们知道sin(666°) = sin(666°- 720°) = sin(-54°) = -sin(54°) 。于是,我们要证明的其实只有sin(54°) = φ/2 。
作一个等腰三角形△ABC,两个底角∠B=∠C=72°,那么顶角∠A自然就是36°。这时作∠C的平分线,交边AB于D。令AD=a,BD=b。所以容易看出△ABC与△CBD是相似的。于是,由图中标志的等量关系,可以得到AB/BC = BC/BD,得到(a+b)/a = a/b。于是a/b就是等于φ。
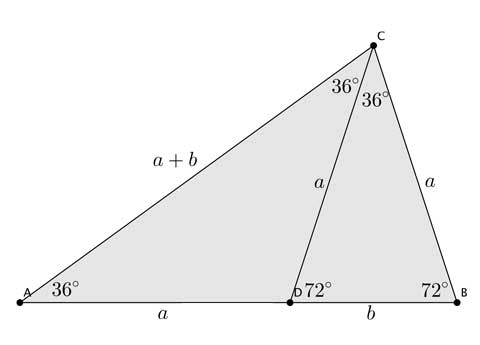
于是,我们取AC的中点E,连接DE。注意到△DAC是等腰三角形。于是∠AED=90°, ∠ADE=90°- 36°=54°。这样,在直角三角形△ADE中计算三角函数 sin(54°) = AE/AD = (2AE)/(2AD) = (a+b)/(2a) = a/(2b) = φ/2 。
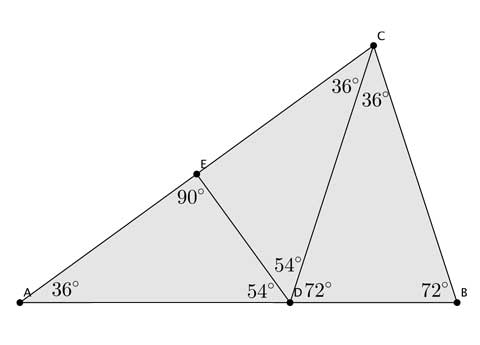
好了!一个漂亮的证明,魔术揭秘完毕!
我觉得用撒旦魔鬼的故事来联系黄金分割比是一个非常娱乐化的例子。稍稍利用简单的数学函数,就能把魔鬼变成天使般美丽的事物。怪不得曾经的主教奥古斯丁还说过这样一句话:“好的基督徒应该提防数学家。这样的危险已经存在,数学家们已经与魔鬼签订了协约,要使精神进入黑暗,把人投入地狱。”
关注微信:DuoDaaMath 每天获得更多数学趣文

评论已关闭