三、四、五边形的数学奇迹
关注微信:DuoDaaMath 每天获得更多数学趣文
作者,Colm Mulcahy ,斯贝尔曼学院数学教授。
翻译,Jacob,哆嗒数学网翻译组成员。
原文地址:http://blogs.scientificamerican.com/guest-blog/martin-gardner-at-101-it-s-as-not-so-easy-as-3-4-5/
著名的科学普及和数学普及作家马丁·加德纳(Martin Gardner , 1914-2010) 名下有101本非虚构类书籍,也有一些虚构类的。如果他还活着的话,在今年10月21日会度过101岁生日。在过去25年中,加德纳为科学美国人上极具影响力的“数学游戏”专栏提供了大量的数学问题。这些问题中的大部分题目衍生出了更多的问题,而不是问题的答案。这实际上是件好事。
时至今日,“数学游戏”专栏以及它带来的对数学娱乐重要性的认知仍在持续产生着影响,加德纳的读者范围也涵盖了几代人。他的铁杆“粉丝”们依然持续举办着两年一度的邀请制的“加德纳聚会”,而其他的任何人(任何地方)在每年十月都可以举办或参加叫做“头脑庆典”的活动。 更重要的是,因为不断提出加德纳难题的新解法和改进旧解法,人们不断地超越自己,突破自己。
接下来,我们怀着轻松的心情,回顾一下加德纳的关于二维平面上图形“剖分”与“平铺”的问题的突破历程——这些曾让大家激动不已的谜题突破历程。值得一提的是,下面有一些结果还是最近才发现的,这让人非常开心,由此证实了加德纳的观点——好玩的数学能真真正正产生的持续不断的研究,更能成为满足好奇心和创造新思想的跳板。
三角形和正方形
“剖分”问题就是把熟悉的图形切开,形成若干个有趣的更小的碎片的问题,而“平铺”问题则要处理与之相对的概念,用大量的某一种或几种特定的小图形来填满一大片空间的问题。
这是加德纳在他1960年2月专栏中提出的一个简单的剖分问题:“给定一个钝角三角形,是否可能将其切成若干个更小的锐角三角形?” 无疑地,最初的数种尝试都失败了,比如下图所展示的(小三角形4不是锐角)
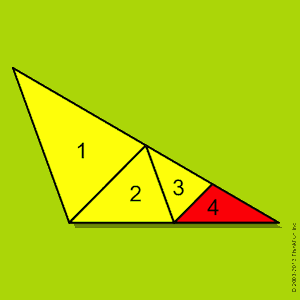
还有一道更难的,选自加德纳1981年4月的专栏:“将一个正方形分割成互不充叠的锐角三角形,那么小三角形的数量最少可以是多少块?”他自己做出了一个令人惊讶的解答。另一个选自1989年的题目问道:“是否可能将一个边长为整数的正方形三角形划分,且划出的三角形每条边仍是正整数?” 这道至今没被解决的题由Richard Guy所提出,他刚刚以一次飞跃阿西尼博因山山顶的直升机之旅庆祝完99岁的生日。 正如Richard在本月的一份电子邮件中评论道,我们仍不知道是否可能在平面上的单位正方形中找到一个点,使得此点与正方形四个顶点的距离都是有理数。
在1958年11月,加德纳提出一个问题,一个正方形是否能够被切成若干个更小的正方形——这些小正方的边长必须为互不相同的整数,而不是类似国际象棋棋盘样子的那种排成方阵简单的形式。从19世纪30年代开始,人们开始了解到这个问题与电网络理论有关联。加德纳提供过的一个近似的答案—— 一个32×33的长方剖分成这样的一些正方形 — 荣登《科学美国人》某月的杂志的封面。

上面的寻找“正方形中的正方形”问题的真正的解答花了20年,其中的一个解是边长为112单位的正方形,它按照要求被切成了21个正方形。加德纳给出过一个有趣的基本论断,来说明为什么这些方式中没有一种可以适用于三维情况—— 就是说一个正方体不能被拆开成为若干的不相等的正方体。自从40年前读到这个论断起,我就深陷其中。这暗示着,在更高维度下,这些方法也不会有用!
从现在起,我们把正方形的问题放在一边,我们来讨论平铺问题吧。在1979年10月,加德纳写出了老友Golomb在1975年提出的挑战问题:整个无限平面是否能被正方形铺满,而且这些正方形边长还是形如(1,2,3,4....)的整数?
Golomb的挑战问题很长时间没被攻破,2008年,它才被Jum Henle 与 他的儿子Fred征服。 Jim解释说:“证明的关键在于一个引理 — “对任意给定L形区域都可以通过添加正方形来使其构成一个长方形。”下面的动画展示了此引理对于28x28的正方形和17x17的正方形组成的L形区域成立的情况。(为了看起来方便,正方形都用3D的正方体来表示)
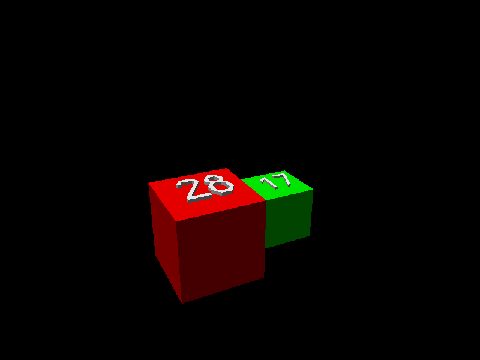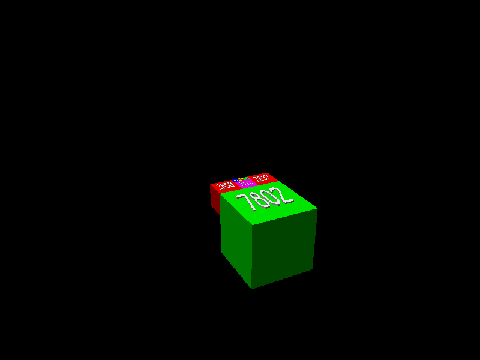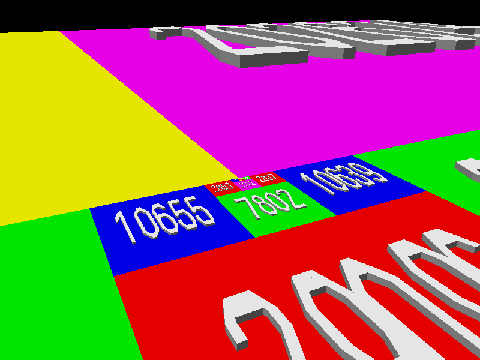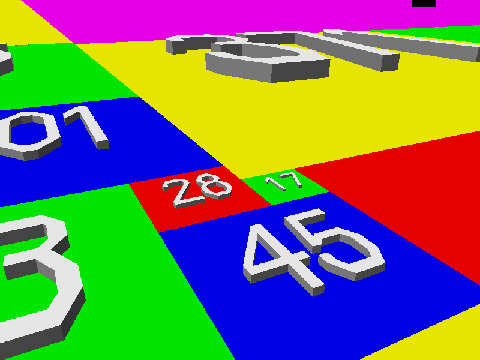
Henle继续说道:“由这个引理开始,证明就很轻松了。因为一旦构成了长方形,你就可以用之前没出现在拼图中的最小的正方形,把它和长方形拼一起,形成一个新的L形区域(这个L形区域也能通过添加更多的正方形被扩大成另一个长方形,而且此做法可以继续下去)。” 因此,每个得整数在拼接过程中都能被不遗漏的选择到,而且最后这个平面(立方体的上表面)将被完全铺满。
在他们论文的结尾,作者对满足相同限制的用三角形铺满平面的可行性进行了讨论。讨论中提及另一个至今待定的问题:“整个平面是否能被所有的有理等边三角形所铺满,而且满足所有三角形相邻的三角形的数量都是有限多个?”
这里说一下另外一个比较扯的趣味智力题,加德纳展示了这个将一个由等边三角形构成的梯形(其实是一个triamond,汉语中没找到对应的词汇)切成四块全等的凸块的剖分方法,并寻求一种用五块全等的凸块分割一个正方形的方法。
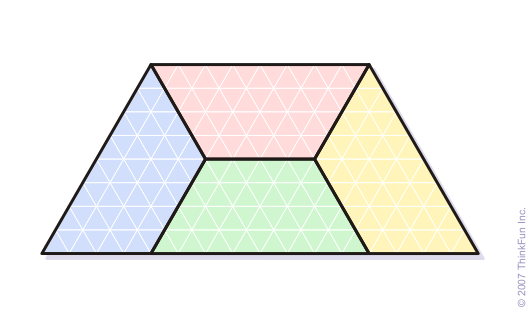
事后看来,答案是相当明显的——我们有提过加德纳也是一个顶级魔术师,也因此是位误导大师么? 就仅在一个月之前,一份“不存在其他解”的证明被公布出来了。(在由Lipin Yuan, Carol Zamfirescu 和 Tudor Zamfirescu所著的“正方形切成五个全等块的分割”的预稿中)
永远令人惊讶的五边形
将三角形和四边形放在脑后,我们来看看五边形。正五边形无法仅靠自身铺满整个平面,而像等腰三角形,正方形和正六边形却能完美的铺满整个平面,不规则的五边形却可以铺满平面。下面的故事的可能都可以在 Wolfram五边形平铺论证计划网页这个互动项目中看到。这个故事在100年前开始,那时Karl Rheinhardt发现了5中不同五边形平铺,这儿有其中的两种。
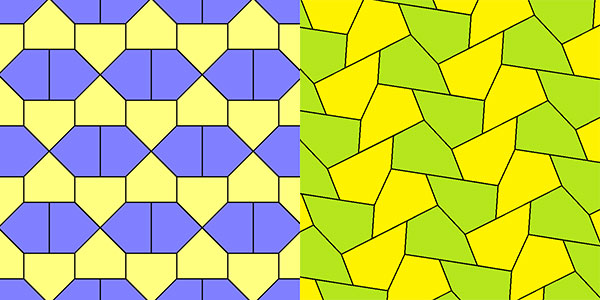
50年之后,在1968年,Richard Kershner发现另外三种形式,并随着Martin在他1975年7月的专栏中的报道,Richard E.James 又发现了一种形式。加德纳及时的在接着的专栏里报道了这件事。而已到中年的圣迭戈的家庭主妇Marjorie Rice在她儿子的一本杂志中读到了这份报告。尽管没受过数学训练,她开始着手探索、组织自己的思绪并开创自己特有的记号来记录自己研究的过程。在1977年之前,通过发现四种全新的五边形平铺平面方法,她令数学界刮起了一阵风暴。这四种方式早先被其他所有人都忽略了,其中的两种展示如下:
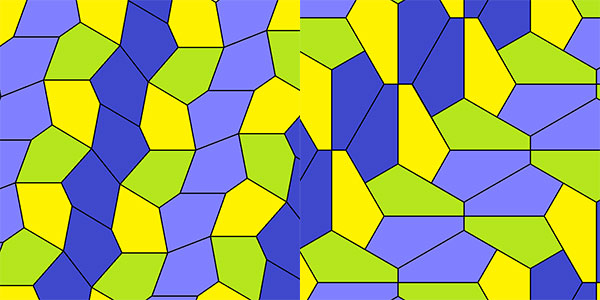
她的一件在1995年发现的成果被数学家Doris Schattschneider采纳,用于华盛顿的美国数学协会本部的瓷砖铺设。

在1985年,Rolf Stein发现一种新的五边形平铺,这将总数目提升到14种。之后又过去了30年,Casey Mann,Jennifer McLoud 和 David Von Derau,这三位都来自于华盛顿大学博塞尔分校的学者,在2015年7月宣布了第15种方法。如下是它的一种体现形式:

下面是所有的15种平面平铺,为了方便比较,像博塞尔团队提供的一样,放在一个新的面板中:

那么还有更多这样铺满整个平面五边形平铺吗?如果还有,一共有多少种这样的平铺呢。博塞尔团队中的印第安人 McLoud(她是她家里第一个拿到大学文凭的人)说:“现在还不知道凸五边形平铺方法数量的上界。”就是说,可能还有几十种,或者有无限种。也有可能就这么多,不再有了。
盖棺了结
仔细看看博塞尔团队五边形是很有建设性的,这个五边形就像一个不规则棺材。也许McLoud和他的同事真的靠着发现最后一种五边形平铺的类型给它钉上了钉子。
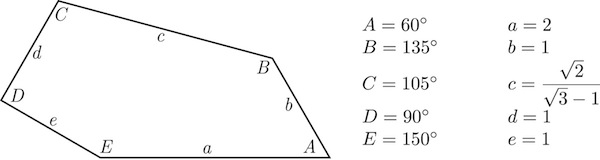
接下来我们来描述得到这个图形的过程:这个形状可被通过折弯一条的5个单位长度的稻草杆子CDEaAB来获得,(这里a代表着图像中线段EA的中点;它也代表着EA的长度),这之后会如下调整:
在右侧,将AB逆时针旋转120°,使得角A成60°。在左侧,将CD顺时针扭成直角,之后保持角D90°的同时,将DE也顺时针旋转30°。EaA保持直线,并且为2个单位长度长。最后,连接将D与B的终点相连:可以看出CB长度为sqrt(2)/(sqrt(3)-1)(sqrt表示开平方),约为1.93个单位长,同时角C和B各自恰好为105°和135°。这个五边形可以被拆解成一个等腰三角形、等边三角形以及一个有着“良好”角度的四边形(分别是三角形DCE、三角形BAa、四边形BaEC)。
一个小孩拿着的稻草杆子瞎捣鼓着把杆子折弯,只要拉开合适的位置,都能轻松地拼出这个五边形。也许,历史的长河中,真有过几次这样的事。如果真有这回事,没有孩子曾意识到他们的发现,他们只会在妈妈叫他吃饭的时候别无他想地扔掉那根稻草杆。那么,又有谁能断定没有某个小孩把稻草杆折成另一种能平铺无限平面的新型五边形呢?他的确是一种孩子能玩的,而且能玩出深入结果的东西(想想前面的主妇)。
加德纳去世后最新出版的这本书无疑即会是老少皆宜的,《注释版爱丽丝》(150周年豪华版,诺顿出版社)。它是将这个畅销书系列的最后一次更新,包含了加德纳在5年去世为止留下的最新的注释内容。
关注微信:DuoDaaMath 每天获得更多数学趣文

评论已关闭