进击的复数
关注微信:DuoDaaMath 每天获得更多数学趣文
作者:逆蝶,哆嗒数学网群友
虚数,是数系中最伟大的发现之一,但是就像无理数的发现过程是坎坷的一样,引入虚数的路途也不是一帆风顺的。在虚数刚出现之时,曾引起数学界的一片困惑,认为虚数是没有意义的,想象的,虚无缥缈的,很多大数学家都不承认虚数。
莱布尼茨曾说:“虚数是神灵遁迹的精微而奇异的隐蔽所,它大概是存在和虚妄两界中的两栖物。”
然而虚数并不是偶然引入的一种虚无缥缈的东西。三次方程求根问题是历史上一个著名的数学问题,一直有数学家尝试给出这个问题的解。直到十六世纪,意大利数学家塔塔里亚才发现三次方程的求根公式。在这之后,虚数的引入就成了一个实际的数学问题,而不再是单纯的一个符号演算。不承认虚数的存在,就意味着无法求解三次方程的根。
虚数出现之后,法国数学家棣莫佛发现著名的棣莫佛公式,欧拉用i表示-1的平方根,将i作为虚数的单位,挪威测量学家韦塞尔试图给虚数以直观的几何解释,高斯对于复素数进行了一系列的研究。再加上柯西及阿贝尔的努力,以及复变函数论的创立,复数理论才比较完整和系统地建立起来,逐渐为数学家所接受。
复数z被定义为二元有序实数对(x,y),记为z=x+yi,其中i是虚根单位。在复数z=x+yi中,x=Re(z)称为实部,y=Im(z)称为虚部。当虚部b=0时,z可视为实数;当虚部b≠0而实部a=0时,z称为虚数,或者纯虚数。
定义两虚数a+bi与c+di的加法:(a+bi)+(c+di)=(a+c)+(b+d)i
乘法:(a+bi)(c+di)=(ac-bd)+(bc+ad)i
根据乘法的定义可得i²=-1,容易验证复数运算和实数运算的运算法则基本相同,只不过是在运算过程中带上符号i而已。
将复数z=x+yi等同于平面上的点或者向量(x,y),那么z有长度sqrt{x²+y²}(这里sqrt表示开根号),称为复数z的模长,记为|z|。复数z'=x-yi,即z关于x轴的对称点,称为z的共轭复数,容易验证zz'=|z|²。另外复数的加法,就等同于向量之间的加法。
记r=|z|,t为z与x轴正方向的夹角,称为z的幅角,那么有x=rcost,y=rsint,于是有z=r(cost+isint),称为复数z的三角表示。欧拉证明了e^(it)=cost+isint,所以也有z=re^(it)(x^y 表示x的y次方),称为z的指数表示。
复数的乘法用三角表示或者指数表示是简单的。通过三角函数的运算可以简单证明若z=re^(it),w=pe^(is),那么zw=rpe^(i(t+s))。也就是说,两个复数相乘所得到的复数,其模是两个复数模的乘积,其幅角是两个复数幅角的和。因此w乘以z,即为w的长度伸缩为原来的r倍,并将w逆时针旋转角度t。
利用e^(πi/2)=cos(π/2) + i sin(π/2)=i,可得一个复数z乘以i所得复数iz可以由复数z逆时针旋转90°得到,这说明复数的确是有几何意义的。
除了以上的几种表示,复数还有矩阵表示。把复数z=x+yi等同于下面形式的矩阵。
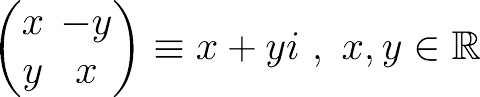
那么容易验证复数的加法与矩阵的加法相容,复数的乘法也与矩阵的乘法相容,而且令人惊奇的是这样的矩阵在矩阵乘法下居然是可以交换的。而复数的模长即为矩阵行列式的平方根,复数的共轭就是矩阵的转置。并且还可以发现下面图片所展示的等同关系。
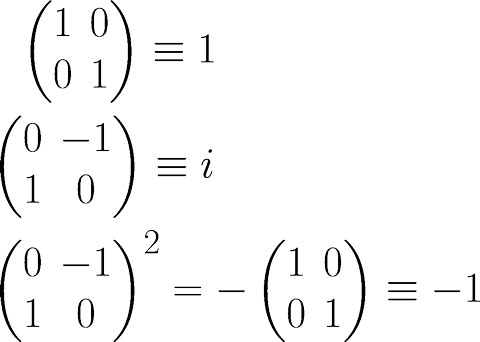
当r=1,即z=e^(it)时,z乘以一个复数w相当于把w逆时针旋转角度t。根据同种理由,称z所对应的矩阵(如下图)为旋转矩阵。
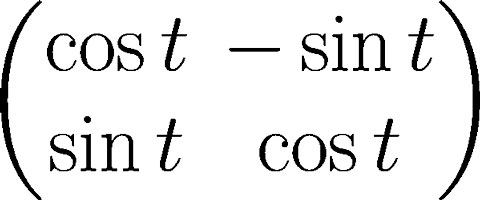
关于复数的减法,自然的定义为(a+bi)-(c+di)=(a-c)+(b-d)i。对于除法,由zz'=|z|²,可以得到1/z=z'/|z|²,这提醒我们可以把复数除法定义为w/z=wz'/|z|²。
这样所有的复数就够成了一个域,称为复数域,复数域是对实数域的扩充。复数域是实数域的代数闭包,也就是说任意的复系数多项式在复数域中总有根,这称为代数基本定理。n次多项式总有根的第一个正确证明是高斯在1799年的博士论文中给出的。
这里对高斯整数做一个简单介绍。每个形如m+ni的复数称为高斯整数,其中m,n是整数。类似于素数,如果m+ni=(a+bi)(c+di)可以得到a+bi或者c+di等于1,-1,i,-i中的某一个数,那么称m+ni是复素数或者高斯素数。显然的关系式5=(1+2i)(1-2i),说明素数5不是复素数,所以素数并不一定都是复素数。确定一个复整数是不是一个复素数,比确定一个整数是不是素数更为困难。另外类似于整数的算数基本定理,复整数也可以表示成复素数的幂相乘。
从实数系到复数系扩充的成功,促使许多数学家考虑复数系的扩充,一般称之为超复数,其中最成功的人物是哈密顿。
哈密顿澄清了复数的概念,这使他能更清楚的思考超复数的问题。他先是寻找三维或三分量的数,并要求具有实数和复数的若干性质。经过若干年的努力之后,哈密顿被迫做出两个让步,一是他所作的新数包含四个分量,二是他放弃了乘法交换律。他称得到的新的数系为四元数,而三元数的不可能性到后来才被人们意识到。
四元数是简单的超复数。复数是由实数加上虚数单位i组成,其中i²=-1。哈密顿考虑复数系的扩充,另外引入两个虚根单位j,k,并有i²=j²=k²=-1。
四元数q被定义为四元有序实数组(x,y,z,w),记为q=x+yi+zj+wk。两个四元数的加法与复数的加法类似,为对应坐标相加。若p=a+bi+cj+dk,q=x+yi+zj+wk,那么p+q=(a+x)+(b+y)i+(c+z)j+(d+w)k。
为了定义两个四元数的乘法,另外规定:ij=k,jk=i,ki=j,这与三维空间向量的外积颇有类似之处。因为ik=i(ij)=i²j=-j,所以根据之前的关系式可以类似得到:ji=-ij=-k,kj=-jk=-i,ik=-ki=-j。
因为ij≠ji,所以乘法不满足交换律。另外由于将i,j,k轮换之后,i,j,k的运算关系式不变,这说明i,j,k的位置是等价的,并没有哪个虚根单位比另一个更特殊,例如完全可以把四元数q写为q=x+zj+wk+xi,从而把z放在第二个坐标。
与复数类似,将q等同于四维空间中的点或向量(x,y,w,k),那么q有长度sqrt{x²+y²+z²+w²},称为四元数q的模长,记为|q|。四元数q'=x-yi-zj-wk,即q关于x轴的对称点,称为q的共轭四元数,容易验证qq'=|q|²。另外四元数的加法,就等同于四维向量之间的加法。
四元数不像复数那样有很好的三角表示,也没有好的指数表示,只有方向余弦q=r(cosα+icosβ+jcosγ+kcosθ)这种较为复杂的三角表示,其中α,β,γ,θ是q与四个坐标系的夹角,r=|q|为q的模长,但是这种表示并不能像复数的三角表示那样可以简化四元数乘法的运算。另外虚根单位i,j,k也可以理解为四维空间的旋转,但是其意义与复数旋转的意义相比较为复杂的多。
四元数有两种矩阵表示。
第一种是复矩阵表示,把q=x+yi+zj+wk等同于下面的矩阵。
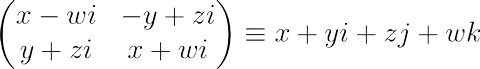
那么四元数的加法与矩阵的加法相容,四元数的乘法也与矩阵的乘法相容,而四元数的模长为矩阵行列式的平方根,四元数的共轭就是矩阵的共轭转置。还有下图的对应关系。这种表示的另外一个好处就是当四元数q=x+yi+zj+wk退化为复数x+yi,即c=d=0时,与之前的复数的矩阵表示是相同的。
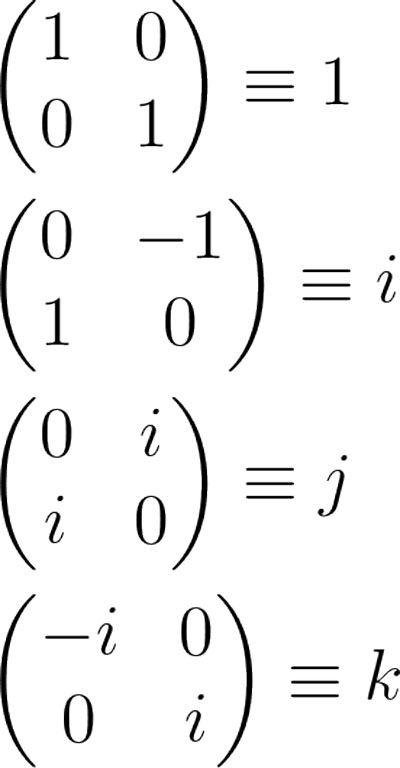
第二种是实矩阵表示,把q=x+yi+zj+wk等同于下面四阶实矩阵。
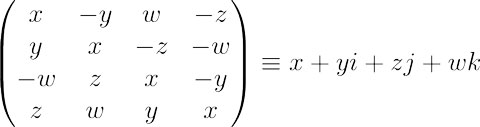
同样的有四元数的模长是矩阵行列式的平方根,四元数的共轭是矩阵的转置。对于退化情形q=x+yi,可见其矩阵表示是复数的矩阵表示放在两个对角块位置上的拼接。
根据k=ij,可以得到q=x+yi+zj+wij=(x+yi)+(z+wi)j,记a=x+yi,b=z+wi,那么q可以视为复数对(a,b),但由于四元数乘法不满足交换律,所以一般的并不满足类似于复数乘法的关系式(a+bj)(c+dj)=(ac-bd)+(ad+bc)j。只有a,b,c,d为实数时,上述关系式才成立。
因为矩阵乘法一般不满足交换律,这也可以帮助理解四元数乘法为什么不满足交换律,所以四元数形成的代数结构称为四元数体,而不是四元数域。关于四元数的减法,理所应当的定义为对应坐标相减。对于除法,由qq'=|q|²,可以得到1/q=q'/|q|²,这说明与复数除法类似,可以把四元数除法p/q定义为p与q'/|q|²相乘。但是与复数不同的是四元数的乘法不满足交换律,所以左乘与右乘是不同的,也即pq'/|q|²与q'p/|q|²是不同的。那么究竟把哪一个定义成除法更合适呢?其实两种定义都是合理的,只需把p和q间除法区分为左除和右除就可以了,即把除法定义为(1/q)·p和p·(1/q),分别称为成左除法与右除法,而不把除法写为p/q的形式。
更一般的,还有数系的关于四元数的扩充,例如Cayley八元数。但是八元数乘法既不满足交换律也不满足结合律,所以其作用与四元数相比有些相形见绌。另外也有许多其他种类的数系的扩充,有兴趣的读者可以查阅专门的文献。
关注微信:DuoDaaMath 每天获得更多数学趣文

评论已关闭