玩扑克洗牌洗几次?
关注微信:DuoDaaMath 每天获得更多数学趣文
作者:小米,哆嗒数学网群友,就读于纽约大学柯朗研究所。
大家打扑克牌时,洗牌一定是一项必备技能。对切法是一种常用的洗牌方法,主要流程是先将牌分成两半,以姆指扣紧牌,使牌弯曲,姆指逐渐松开内向拨牌,使兩叠牌交錯叠在一起(注1)。
今天我们就要问一个数学上的问题:用对切法要洗多少次牌才能把一副牌洗均匀呢?
回答这个问题分为两部分:第一部分是给出对切法洗牌的数学描述,第二部分是给出“洗均匀“的数学定义。为了讨论方便,我们假设一副牌有n张牌,而把我们的结果用到现实中时,n=54。
我们先把对切法洗牌过程数学化。
假设我们把一副扑克牌牌面朝下放置。
对切法洗牌分为两步:
第一步我们需要把牌分成两堆,第二步是把两堆牌按某种方式混合在一起。
现在我们在第一步中的两堆牌分别称为“上牌堆”和“下牌堆”,并把上牌堆中的牌标记为1,下牌堆中的牌标记为0。
设上牌堆里有k张牌,也就是说有k张牌被标记了1,(n-k)张牌被标记为0。这样,当我们完成一次洗牌后,从上往下观察牌堆,将会看到一个0和1组成、长度为n的序列,其中恰好有k个1和(n-k)个0。
我们可以把上面的过程逆过来,称之为一次“逆洗牌”。
一次逆洗牌对应着顺序相反的两步:
第一步,给牌堆中的每张牌标记上0或1;
第二步,把标记为1的牌从牌堆中抽出,并保持原来的相对顺序整体叠放在标记为0的牌的上方。
因此,每一种对切法洗牌(由上牌堆数目之多少,以及以何种方式混合两堆牌决定),与一个长度为n的0、1序列一一对应。
下面我们给出一个理想化的对切法洗牌,其对应的长度为n的0、1序列是随机生成的。也就是说,在逆洗牌的第一步中,对牌堆中的每张牌,我们以1/2的概率标记为1,以1/2的概率标记为0。
这种洗牌方式又称作GSR(Gilbert-Shannon-Reeds)洗牌法。一次GSR洗牌是一种特殊的对切法洗牌。
在第一步中,上牌堆的牌数为k的概率是C(n,k)/2^n(注2),这恰好是给n个数随机赋值0和1,恰好有k个1和(n-k)个0的概率。
根据概率中的中心极限定理,k大概服从N(n/2,n),即均值为n/2,方差为根号n的正态分布;也可以说,几乎就是平均地把牌分成两堆。
在第二步的混合中,我们在牌堆的n个位置中随机选取k个位置,然后把上牌堆的牌保持原来的顺序放入这k个位置中;然后再把下牌堆的牌保持原来的顺序放入余下(n-k)个位置中。可以说,GSR洗牌既很好地模拟了实际情况,数学上又十分简单。
进一步,我们可以考虑连续m次GSR洗牌的逆过程。
我们把m次GSR洗牌前扑克牌的顺序称作“初始牌序”,把m次GSR洗牌后的顺序称为“最终牌序”。那么连续m次GSR洗牌的逆过程,就是从一个最终牌序还原出初始牌序的过程。
那么m次GSR洗牌的逆过程是怎样的呢?
经过简单的思考,我们发现我们需要对每一张牌随机指定一个长度为m的0、1数组,数组的第一个0或1表示这张牌在第一次洗牌时这张牌来自于上牌堆还是下牌堆,第二个0或1则表示第二次洗牌时这张牌来自上牌堆还是下牌堆,以此类推。
我们举一个例子,假设有5张牌,2次GSR洗牌后得到的最终牌序是DBACE,现在我们给每张牌指定一个长度为2的0、1数组如下
D: (0,1)
B: (1,0)
A: (1,1)
C: (1,0)
E: (0,0)
当然,如果指定的0、1数组不一样,还原出来的初始牌序也不同。让我们先看看对于上述的0、1数组,初始牌序是怎样的。
第1次逆洗牌我们需要看这5个数组的第2个分量,它们表征每张牌在第1次逆洗牌中(对应着第2次洗牌)被分到上牌堆还是下牌堆。由于AD的第2分量为1,BCE的第2分量为0,所以进行第一次逆洗牌后,我们得到DABCE。
第2次逆洗牌我们需要看数组的第1分量,由于ABC的第一分量为1,DE的第1分量为0,所以我们应当把ABC移到前面,得到ABCDE。(当然啦,这个例子是经过设计的,不然也不会这样巧得到ABCDE。)
当我们再仔细思考这个过程,发现m次逆洗牌可以一次性完成!
如果我们把一个长度为m的0、1数组通过二进制对应一个0~(2^m-1)整数,如下
D: (0,1) --> 0*2 + 1 = 1
B: (1,0) --> 1*2 + 0 = 2
A: (1,1) --> 1*2 + 1 = 3
C: (1,0) --> 1*2 + 0 = 2
E: (0,0) --> 0*2 + 0 = 0
那么我们可以这样一步到位完成m次逆洗牌:先把最大的整数3对应的A称到最前面,再把整数2对应的BC紧接着A后面(这时有两个字母B和C对应着相同的整数2,必须保持B和C在最终牌序DBACE中的相对顺序),然后把整数1对应的D移到ABC后面,最后把0对应的字母E移到ABCD后面。瞧,我们又得到了ABCDE!
一般的来说,一次性完成m次逆洗牌分为两步。
第一步,“指定数字”:每张牌随机指定一个0~(2^m-1)中的整数。
第二步,“重新排序”:按每张牌被指定的数字大小,从大到小重新排列所有的牌;如果出现多张牌被指定的数字一样,那么在排列时必须保持原来的顺序。
值得指出的是,m次GSR洗牌与m次逆洗牌有一一对应关系,也和n张牌被指定0~(2^m-1)中整数的不同方式一一对应。由乘法原理,一共有2^nm种指定整数的方法,因此也有2^nm种完成m次GSR洗牌的方法,同时,这2^nm种方法都是等可能的,概率为1/2^nm。另一方面,对于同样的初始牌序和最终牌序,也有可能对应着多种洗牌方法。
完美解决了第一个问题后,接下来我们得弄清楚,究竟怎样才算是“洗均匀”呢?
我们先感性地认识一下这个问题。
在一次性完成m次逆洗牌的过程中,我们看到当有两张以上的牌被指定了同样的整数时,它们在初始牌序和最终牌序中的相对顺序会完全一样。而我们也看到,当m足够大时,为n张牌指定的n个0~(2^m-1)中的整数很可能两两不一样,这样,初始牌序和最终牌序就完全无关了。因此,一个合理的洗牌次数m,应该使得有一定的概率(例如25%)能够使n张牌被指定的整数完全不一样。
在数学上有,这样一个生日问题与此非常类似。假设一个班上有N个人(如N=30),假设每个人的生日都是独立的,问任意两个人的生日都不相同的概率有多大?
我们可以这样考虑这个问题。给N个人编号1,2,...,N。
第1个人的生日可以随便选取;第2个人的生日为了避开第1个的生日,只能从剩下的364天中选择;第3个人的生日为了避开前2个人的生日,只能从剩下的363天选择...
最终根据乘法原理,N个人的生日全部不相同的概率由(1-1/365)(1-2/365)...(1-(N-1)/365) 给出,当N不太大时,约等于(1-1/365)^N。
回到我们的洗牌问题。我们需要为n张牌中的每张牌指定一个0~(2^m-1)中的整数。那么所有被指定的整数都不一样的概率有多大呢?这时“生日”数相于2^m;而N相当于总的牌数n。根据前面的公式,n个“生日”全部不等的概率约等于(1-1/2^m)^n。
根据微积分中的重要极限 (1-1/x)^x=1/e,x→∞,我们得知,为了使(1-1/2^m)^n不是一个太小的数(在数量级的意义上,例如我们可以认为0.01是比较小的数,而0.1是相对比较大的数),必定有2^m和n差不多大。这样我们得到了第一个估计:2^m > n,也就是m>log_2 n。
在n=54时,log_2(n)大概是5.5。至少我们的感性认识给出了洗牌次数的正确的数量级!
为了更精确地给出数学上“洗均匀”的定义,我们引入两个概率分布的距离的概念。
对于两个概率p和q,对应的分布列分别是(p1,p2,...,pN)和(q1,q2,...,qN),那么我们定义它们之前的(全变差)距离为d(p,q)=|p1-q1|+|p2-q2|+...+|pN-qN|。
这怎么应用到我们的洗牌问题上呢?
首先,不妨总是假设我们给n张牌编号为1,2,3,...,n,并且初始牌序就是1,2,...,n。最终牌序则由一个{1,2,...,n}到{1,2,...,n}的双射h给出:
对于编号为i的牌,经过m次GSR洗牌后,它的位置变成了第h(i)张牌。我们常常也以同样的字母h表示一个最终排序。
我们知道n张牌一共有N=n!种排序方式。通过m次GSR洗牌,h显然就是这N种排序方式的其中一种。事实上,h以一定的概率得到给定的一个排序方式,这其实是对应了一个分布列(p1,p2,...,pN),表示h取每种排序方式的概率。另一方面,我们可以考虑另一个分布列(1/n!, 1/n!, ..., 1/n!),这表示每种排序都以相同的概率1/n!出现。
显然,我们可以定义把“洗均匀”定义成两个概率分布p和q的距离d(p,q)足够小(这里的“足够小”可以理解为,如小于1/2)。
接下来,我们的问题就转化为,对于一个给定的最终牌序h,从1,2,...n的初始牌序出发,通过m次GSR洗牌,得到h作为最终牌序的概率(记为p(h))有多大。
由于m次GSR洗牌的2^nm种洗牌方式都有相等的概率1/2^nm,我们只需要计算有多少种GSR洗牌方式,能从1,2,...n得到h。等价的,我们只需要计算有多少种逆洗牌方式,能从h得到1,2,...,n。
现在我们用f(i)表示编号为i的牌,在逆洗牌的第一步“指定数字”中,被指定的0~(2^m-1)中的整数。f可以看作一个从{1,2,...,n}到{0,1,2,...,2^m-1}的函数。
现在我们的问题是,对于给定的最终牌序h,有多少个f能把h通过m次逆洗牌变成1,2,...,n呢?
我们还是先考虑怎样从DBACE通过2次逆洗牌得到ABCDE。
为了得到ABCDE,显然我们要有f(A)>= f(B) >= f(C) >= f(D) >= f(E),也就是说f是一个减函数。
其次,由于在最终牌序中,A在B之后,所以f(A)不能等于f(B),因此f(A)>f(B);同理,C在D之后,我们也必须有f(C)>f(D)。可以验证,只要f满足f(A) > f(B) >= f(C) > f(D)>= f(E),我们都可以从DBACE通过2次逆洗牌得到ABCDE。
现在问题就转化为,求所有函数{1,2,3,4,5}到{0,1,2,3}的函数f(我们把A和1等同,B和2等同,以此类推),使得f是减函数,并且在f(1)和f(2)、f(3)和f(4)之间的严格减函数。事实上,我们可以把f稍加变形,变成一个严格减函数。
令g(1)=f(1)+2, g(2)=f(2)+2, g(3) = f(3)+1, g(4)=f(4)+1, g(5)=f(5),那么g是一个从{1,2,3,4,5}到
{0,1,2,3,4,5}的严格减函数,并且每一个这样的g和我们要求的f一一对应。显然,这样的函数g的个数与在{0,1,2,3,4,5}中选取5个不相等的整数的方法数一样,用组合数给出就是C(6,5)=6。
我们把上面的情况推广到一般的n和最终牌序h。首先f必须是一个减函数。如果h(i)>h(i+1),也就是说标号为i的牌在最终牌序中位于标号为i+1的牌之后,那么f(i)必须严格地大于f(i+1),即f(i)>f(i+1)。
现在我们定义h对应的“逆序量”R=R(h)为所有满足h(i)>h(i+1)的i的个数。那么满足条件的函数f的个数,与所有从{1,2,...,n}到{0,1,..., 2^m-1+R}的严格减函数g的个数相等,进一步地,与{0,1,...,2^m-1+R}中选取n个不同整数的方法数相等。因此,满足条件的f一共有C(2^m+R, n)个。
于是,得到最终牌序h的概率为
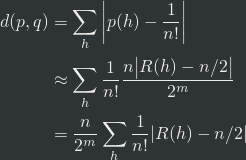
这里我们用到了一个近似:当x1,...,xk很小时,(1+x1)...(1+xk)约等于1+x1+...+xk。
进一步我们得到全变差距离为
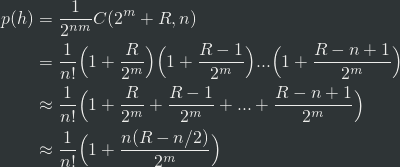
上面和式中的最后一项,正好是当h等概率地从n!种所有可能排序中随机选取时,其对应的逆序量与n/2偏差的期望。
更进一步的分析其实可以得出,R(h)几乎服从N(n/2,n),即均值为n/2,方差为根号n的正态分布。因此逆序量与n/2偏差的期望约等于根号n。这样我们得到d(p,q)约等于n^(3/2)/2^m。
由n^(3/2)/2^m < 1/2我们得到m> 3/2* log_2(n) +1。当n=54时,这个数字大约是9.6。
当然啦,有一种说法是洗牌洗7次,洗7次牌也仅仅是个约数罢了,也许就是叫得比较顺口吧。通过不同的计算表明,洗牌少则5、6次,多则9、10次,就能把牌洗得很均匀了。同时我们的计算还表明,洗牌次数只取决于n的对数。也就是说洗2副牌,也只需要比洗一副牌多一两次足矣!
注1:描述来自维基百科https://zh.wikipedia.org/wiki/%E6%B4%97%E7%89%8C
注2 :C(n,k) = n!/k!(n-k)!为组合数。
关注微信:DuoDaaMath 每天获得更多数学趣文

评论已关闭