几何是世上最美丽的艺术
关注微信:DuoDaaMath 每天获得更多数学趣文
原文作者:Dan Rockmore
译文作者:e^iπ+1=0,哆嗒数学网群友,就读于上海科技大学。
我参观了两个在曼哈顿西区展出的展览,展览将数学和视觉艺术很好的结合起来。一个是在惠特尼美术馆展出的弗兰克•斯特拉回顾展,另一个是在南希霍夫曼画廊展出的一个画展。如果你喜欢艺术与数学的结合(正是艺术教我们如何从“STEM(科学、技术、工程、数学)教育”转变为“STEAM(科学、技术、工程、艺术、数学)教育”!),而且若你有些精力漫步于数学艺术中,那我推荐你可以去纽约现代艺术博物馆游览。
在我看来,纽约现代艺术博物馆经常将与数学相关联的展品放在一起,其中有一些很显然,但有些则不容易看出。这一次的展览中,两种类型的展品都有所展示。对于前者来说,可以看一看无尽之屋(Endless House)这个优美的小型展览,其中展示了很多建筑模型,其中一些房屋的设计灵感来源于甚至取名于一些基本的数学对象,如环面(如普林斯顿•斯科特•科恩的《环面屋》(Torus House))和莫比乌斯带(鲍斯/范•伯克的莫比乌斯的房子)
事实上,几何学的灵感和美感(除了明显的在工程上与数学的联系)对建筑的影响有很长的一段历史,早在古希腊时期,就已经将经典的几何形状如正方形和圆形应用到他们的结构中去了。无尽之屋这样的展品明显表明这样的影响还在延续。
谈及展览的名字,无论环面还是莫比乌斯带,其实都是有限实体也可以创造无限的例子。圆环可以说是数学家的结婚戒指,而且被许多人认为是无尽之爱的最好的典范。而莫比乌斯带从另一方面来说,是一枚扭曲的婚礼戒指。更精确地说,取一条纸带,先拉直,再半扭曲,最后将两个相反的终端相接,并且从连接的一端开始使之成为一圈。如果你是一只蚂蚁,那当你回到连接点的边界,将会完全颠倒过来。继续走直到你再一次回到出发点,你又会颠倒,重新回原来的状态——也许这是一个关于婚姻的隐喻。假如你是一只沿着中线爬行的蚂蚁,最终会发现你处于颠倒的状态。无论方向是保持不变还是反转,在有限的空间里都会给出无限的感觉,而这无疑是建筑上和数学上的期望。
几何主题也在其他两个正在展出的优美展览中延续——但是这些作品中数学并不是很显而易见,虽然在很多情况下这更加迷人:在纽约现代艺术博物馆的二楼你可以发现一个简洁但富有思想的展品,这是来自于杰克逊•波洛克的作品,以及在角落里一个一鸣惊人的雕塑作品,来自于巴勃罗•毕加索。现在我将试着阐述当我行走于这些展品间,通过数学的眼光我看到了些什么。
波洛克因其“滴色绘画”而被众人知晓,它是通过将颜料抛洒到放在工作室地面上的画布上完成的。波洛克会在画布上舞动,同时巧妙地指挥刷子上的油料,犹如芭蕾舞舞蹈一般,所以他被认为是最初的“滴色派画家”。他认为作品最好的状态是自身意图和意外惊喜的奇妙杂糅(即使在移动中,他仍旧对画作有艺术名家般的控制),画布上记录着他的行动和创想。
在波洛克很多的作品中都可以看出“随机”——这是一些无法辨识的图形——但事实上,在数学小小的帮助下,波洛克作品中的很多随机程度都是可以被量化的。在1995年,物理学家理查德泰勒发现可以用数学上的分形集合来研究波洛克的工作。一幅“分形的图像”可以被描摹为它可以惊奇地出现在自身每一个比例的图像中,当我们越来越细致的观察它,它永远不会被完全“填满”,而不能被填充的原因是其所具有的某些规律性质。也就是说,如果你使用一台显微镜去观察分形图像,即使你提高它的放大能力,也不可能看到一个点,而是看到难以名状的一团图像。当然,在图像上会有很多的洞。此外,无论你怎么看,从物镜看到的区域总是和总体保持一致性。你可以计算这个图像的维度。鉴于直线是一维图形,被填满的区域是二维图形,波洛克作品的维度看上去像是介于这两者之间。这就是说处于分形维度。数学家曼德布罗特发明了“分形”这一概念去描绘这些结构,并且在各种不同的自然(甚至经济)现象——从海岸线到山脉,从树叶到花椰菜茎。当被问及他的工作过程时,波洛克因其他说“我是自然的”而著名。从数学的角度上来说他是非常正确的。

有趣的是,泰勒是从他的艺术作品中获得了这个灵感:那还是他学习艺术时在一年的休假中所做的最终作品的一部分。泰勒建构了精巧的装置使得利用风来完成他的画作。他注意到自己所创作的画作和波洛克的滴水画作有一定的相似度,此外,他知道风的运动(湍流)可以产生分形现象(想想从烟囱里飘出的炊烟被风吹成涡流的形状)。泰勒的作品想来饱受争议——特别是将他的画用作认证波洛克的画(他曾经有一段时期是波洛克-克拉斯纳基金会的顾问)—— 但分形的计算和其数学联系非常吸引人去探索。
现在在纽约现代美术博物馆的大作应当是毕加索雕塑展览。众所周知,毕加索通常被认为是“立体主义”的创始人,这是一项二十世纪初发起的艺术运动,倾向于用直觉解构物体的表现,它通常是在单幅作品中堆叠融合各种视图。通过这种方式将三维模型直观地转为多个二维视图的重构。在上一次的展览中我们认识到毕加索“可以灵活运用多角度的观点”。立体主义因此成为一个立体视觉的艺术探索,它通过将左右视网膜上独立的二维图像进行整合从而来产生三维体验。《女人头像》(巴黎,1909),毕加索早期最有名的雕塑,被认为是他的立体主义大作,体现了二维堆叠的想法。从为这次展览所写标签文字中可以知道,破裂面和翻光面构成了雕塑的表面,这也标志着这是一个媒介上对立体主义的一种探索。

通常来说,立体主义的历史呈现为塞尚平面画作的自然进化。但这里又有另一个有趣的故事,有人注意到数学和物理学上同时期的发展,发生在相对论这一跨世纪的发现,其中大量使用了四维思想,为理解世界打开走出了一条新的路。在《爱因斯坦、毕加索:宇宙、时间、和动人心魄之美》一书中,科学史家亚瑟•米勒认为在毕加索的智慧结晶中相对论的发现还有很多值得深究之处,这是围绕思考四维的神秘与复杂的普遍思潮的一部分。
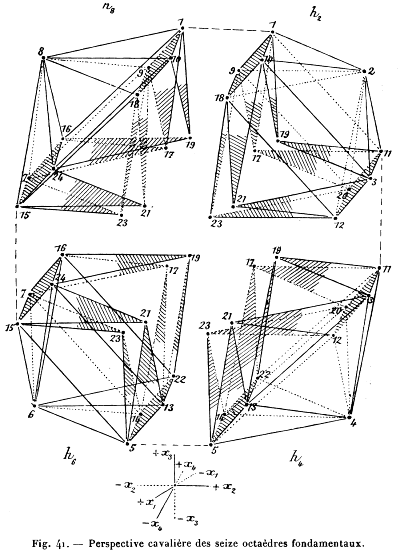
米勒在Espirit Jouffret的关于四维几何的通俗读物(《初论四维几何》1903年)与艺术建立了有趣的联系(通过莫里斯•潘塞,是一个保险推销员,也是毕加索认识的熟人)。在书中他通过多重的二维投影和三维投影来阐释四维物体,而不是用一堆平面视图来表现三维实体。Jouffret的直观解释,比如以下这张图,用以解释超立方体,从我的角度来看,这暗示了很多早期立体派作品Jouffret不是唯一一位为大众创作关于四维的书。在英吉利海峡的另一端,艾特温•阿博特,其著名的数学书籍《二维国》用不同的方式拟人化了四维。《二维国》部分是数学普及读物,部分是社会评论与讽刺作品(包括对几何元素卡通般的拟人化,从高傲的多边形到谦卑的点)。它阐释的方法是通过类比在二维平面生活的人类的视觉体验,将三维的读者投放到四维空间中。这些二维国的生物生活得犹如悬浮在最细的纸张里。就其本身而言,他们没有办法感知上下或者离开纸张,而我们也仅仅只是能想象离开我们所存在的空间。二维国里的生物可以被认作是封闭的,被嵌在纸张里。然而,作为二维国外的观察者——当我们观察纸张时——事实上我们能看到这些生物的内部!类似的,一个存在在四维空间的人同样也可以“识透”三维实体。
从这个角度上,让我们现在再回到毕加索展。在展览的二号房间我们发现了毕加索另一幅最为著名的作品,《吉他》(1914)这—不是对乐器的简单复制,更确切的说是同时展示吉他的内部和外部。也暗示假如这吉他存在于四维时空,或许有人会拥有这种吉他。

几何学这门学科,脱胎于人类想要理解周遭世界的渴望。我偏向于认为艺术至少有一部分是出于同样的动机。这个月在纽约艺术博物馆,可以来看看数学和艺术是如何以令人惊讶的和美丽的方式走到一起。若你真的有机会来这里欣赏艺术,且持有一份开放的心态,当你行走其中,比如沿着莫比乌斯带旅行,离开时你会发现自己正在思考数学。
关注微信:DuoDaaMath 每天获得更多数学趣文

评论已关闭